受AdaBoost启发的Margin Theory间隔理论

到底什么是AdaBoost？用动画和代码的方式，最清晰讲解！_哔哩哔哩_bilibili

这个视频直观的解释了AdaBoost是什么，和它为什么效果这么好

【报告】Boosting 25年（2014周志华）（up主推荐）_哔哩哔哩_bilibili

这个视频周教授深入的探讨了AdaBoost到底为什么效果这么好，模型迭代过程中到底是在优化什么。从这方面引申出了间隔理论的提出，争论，以及最后是如何完善的。

决策树可以简单直观高效的分类样本，不过单个决策树往往会因为样本的复杂性而增加模型复杂度，在树变的很深的时候很容易过拟合。

最简单的（集成学习）优化方法就是bagging - 随机森林将样本空间进行拆分/随机采样成不同的训练子集，并行训练几个不同的决策树（强学习器，i.e. 直接去尝试对整个样本空间去进行拟合），最后通过投票/平均值来给出最终答案。

这么做最明显的好处就是模型的泛化能力更强了，更robust稳定了，方差Variance也降低了，但是相对的是对于样本空间被错分的样本缺乏关注，也就是偏差Bias提高了。

基于Bias-Variance Decomposition，我们知道均方误差MSE可以分解为 Expected Error = Bias^2 + Variance + Irreducible Error 其中 不可约误差是数据的噪声，也叫贝叶斯误差。

我们可以看到，想要降低均方误差（期望误差），我们就要降低Bias^2 + Variance，又因为Bias和Variance在模型训练过程中是相对的：降低Variance不可避免地要提升Bias，反之一样。所以处于平衡点的模型基本属于最优模型。

另外一个优化boosting - AdaBoost串行的训练决策树（单层最简决策树），和随机森林相比，与其训练几个复杂的模型，每一个都有不少误差，然后通过平均值/投票来尽量的抹平误差，AdaBoost直接在训练的过程中减少误差，当然不可避免的方差就比随机森林要略高了。

下面内容来自周教授的讲座视频

Kearns和Valliant先是在STOC’89提出 可弱学习（存在准确率大于50%的模型）是否等价于可强学习（存在一个精度接近100%的模型）。

然后1990年Schapire从数学上证明了他们是等价的。

1997年，Schapire和Freund给出了可应用的算法 - AdaBoost。

基本来说，AdaBoost通过给前面分类错误的样本添加一个指数级大的权重，来影响下一次模型迭代”分界线“，这样模型就会尽可能地尝试将这些之前被分类错误的样本正确的给分类出来。这样我们就可以看到：最影响模型边界的样本往往是那些很容易/一直被错误分类的样本，类似于SVM的Support Vectors。

AdaBoost最著名的一个应用就是人脸检测的Viola-Jones检测器（基于Haar特征），它前几个阶段先只用AdaBoost的前几个弱分类器去检测人脸是否存在，通过了才会运行后面的弱分类器，这样大大的减少了计算量。

AdaBoost也是现在基本所有boosting算法的基础，AdaBoost奠定了此类算法的核心机制，优化AdaBoost相当于优化所有基于AdaBoost的boosting算法。

现在考虑从数学上观察AdaBoost的准确率。

Schapire和Freund在1997年给AdaBoost了一个上界，只要每个弱学习器的准确率严格大于50%，并且弱学习器的准确率不会随着迭代趋于50%，那么训练错误指数级减少，且有上界 e^−2Tγ2, T是迭代数量，γ是0.5 − ϵ_t ≥ γ, γ > 0, ∀t ∈ [T]。

当然训练误差只能表明模型对于现有数据的拟合度，不能作为模型泛化能力的估计。他们也给出了泛化误差：在1 − δ概率下$$\epsilon_{\mathcal{D}}\le\epsilon_D+\tilde{O}\left(\sqrt{\frac{dT}{m}}\right)$$其中𝒟是测试数据集，D是训练数据集，d是弱学习器的VC-dimension（模型越简单d越小），T是迭代数量，m是样本数量，Õ省略了其他变量。

我们可以看到这里的上界，AdaBoost迭代次数越多，上界越大，这里是否表示了AdaBoost随着迭代次数增加会逐渐过拟合模型？

从测试误差的数据上来看，AdaBoost并不会过拟合。这算不算是违背了奥卡姆剃刀原理（最简单即最好）？

这里有两种流派尝试解释这一现象：

• Margin Theory（Schapire, Freund, Bartlett & Lee, 1998）
• Statistical View（Friedman, Hastie & Tibshirani, 2000）

Statistical View

Ann.在2000年指出AdaBoost可以近似成对additive model $H(x)=\sum_{t=1}^Ta_th_t(x_t)$的logistic function来预测概率，用牛顿法对指数/对数损失函数进行优化

ℓ_log(h|𝒟) = 𝔼_{x ∼ 𝒟}[ln (1 + e^−2f(x)h(x))]

从这个角度出发，衍生出了很多其他boosting算法，通过其他方法来优化对数损失函数，如LogitBoost LPBoost L2Boost RegBoost。

问题是，Statistical View就是解释不了为什么AdaBoost不会过拟合，很多理论也和现实数据冲突。

比如说，这个观点解释不了为什么VC-dimension增加（从单层决策树变为8节点树）会拟合的更好；LogitBoost理论上有噪音的时候比AdaBoost要好，但是结果上是反过来的；还有最重要的，模型早点停止可以防止过拟合，但事实上不停也不会过拟合。

Margin Theory 间隔理论

在机器学习方法，模式识别与机器学习，和周教授的西瓜书里，关于AdaBoost也都只是介绍了上面的观点。间隔理论虽然在统计学中没有明确的定义，但是在实际应用中发现理论都是没问题的。

这里AdaBoost的间隔理论和SVM的区别是，SVM是完全基于间隔理论进行的算法优化设计，而AdaBoost仅仅是套一个间隔理论模型的壳来（启发性的）解释为什么AdaBoost优化的没问题，这里AdaBoost实际优化的并不是间隔。

二元分类本质上都可以看作是把数据找一个超平面拆分开来，我们可以认为间隔margin（超平面两边距离决策边界的和）越大，我们分类的把握性就越大。

Schapire et al.在1998年基于间隔理论给出了一个新的上界 $$\epsilon_{\mathcal{D}}\le\mathbb{P}_{x\sim\mathcal{D}}(f(x)H(x)\le\theta)+\tilde{O}(\sqrt{\frac{d}{m\theta^2}+\ln\frac1\delta})$$$$\le 2^T\prod_{t=1}^T\sqrt{\epsilon_t^{1-\theta}(1-\epsilon_t)^{1+\theta}}+\tilde{O}(\sqrt{\frac{d}{m\theta^2}+\ln\frac1\delta})$$ 其中θ是间隔。可以看到样本数量m越大误差越小，模型复杂度越小误差越小，还有间隔越大误差越小。

上面的Õ展开来是$O\left(\frac{1}{\sqrt{m}}\left(\frac{\ln m\ln |\mathcal{H}|}{\theta^2}+\ln\frac1\delta\right)^{1/2}\right)$，可以看到是$O(\sqrt{\log m/m})$。

所以。基于最小间隔的想法，Breiman在1999年提出了一个更紧的上界：$$\mathbb{P}_{\mathcal{D}}(yf(x)<0)\le R(\ln(2m)+\ln\frac1R+1)+\frac1m\ln\frac{|\mathcal{H}|}{\delta}$$ 其中$\theta>4\sqrt{\frac{2}{|\mathcal{H}|}}$和$R=\frac{32\ln 2|\mathcal{H}|}{m\theta ^2}\le 2m$可以看到是O(log m/m)。

由于log m/m < 1, Breiman确实给出了一个更紧的上界。换句话来说，如果用同样的训练样本（数量m），那么Breiman的上界比Schapire的更准确一些。

于是，基于这个理论，Breiman同时设计了一个基于AdaBoost的变种arc-gv，通过直接最大化最小间隔来优化算法（类似于SVM了）。问题是实验结果看下来虽然minimum margin确实是比AdaBoost更大了，但测试误差也变大了许多。

这就说明了，minimum margin 无法解释为什么AdaBoost效果这么好。

Reyzin和Schapire深入的研究了Breiman的arc-gv，发现这个模型的VC-dimension虽然是固定的，但是实际上还是和AdaBoost的stumps单层决策树有区别。这个区别就影响了实验结果。

当他们把arc-gv的弱学习器也变为decision stumps单层决策树（树墩），就看到arc-gv虽然minimum margin最大，但是更关键的margin distribution更差了。这里他们就发现了，比最小间隔更重要的是平均/中位间隔，分布比极端数值更重要。

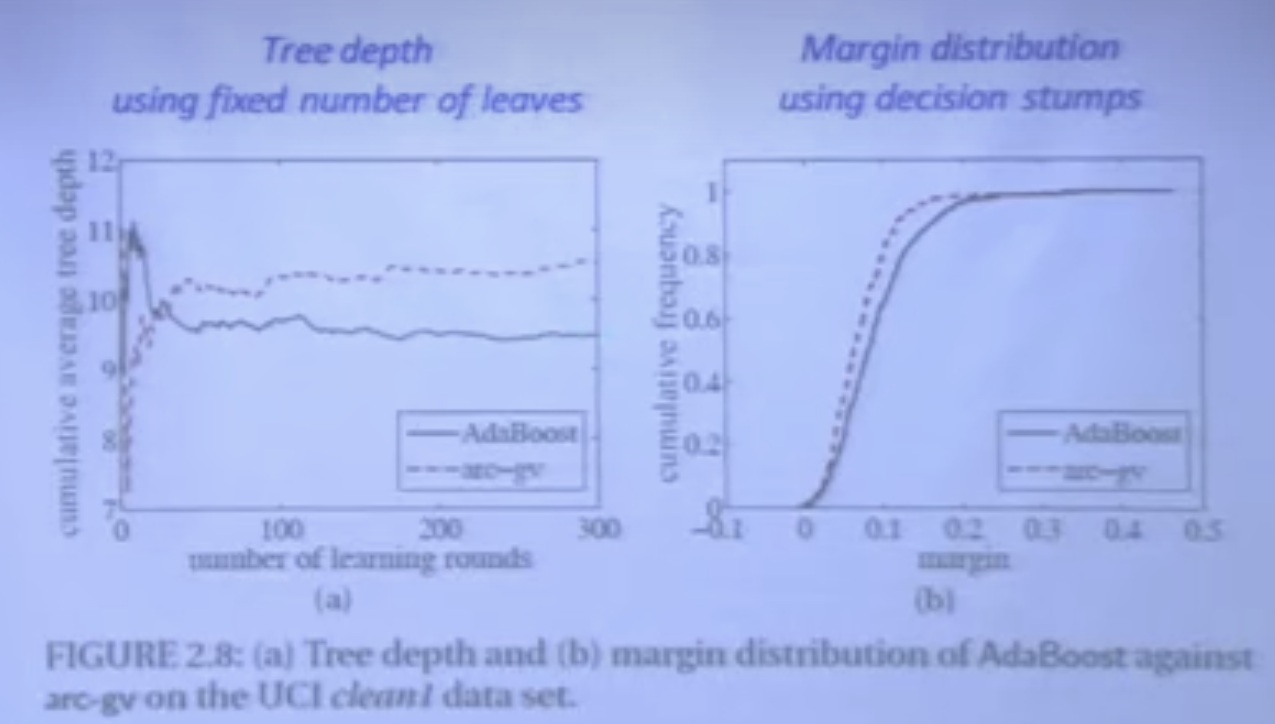
Wang et al.在2011给出了一个具体的基于margin distribution的更紧的上界（这里的margin称之为Emargin），也是O(log m/m)，不过问题是这里的界过于复杂，而且考虑了比前面Breiman和Schapire更多的信息，比如说KL散度，所以光从这个界上判断，无法知道这个更紧的界更紧是因为获取的信息更多了还是因为margin distribution比minimum margin更本质。

Gao&周教授在2013提出了一个新的margin bound，叫kth margin bound，并指出前面的minimum margin和2011提出的Emargin都是属于kth margin bound的一个特例，都不能真正的代表margin distribution。并且，给出了一个真正的margin distribution的界：

$$\mathbb{P}_{\mathcal{D}}(yf(x)<0)\le\frac2m+\inf_{\theta\in(0,1]}\left[\mathbb{P}_S(yf(x)<\theta)+\frac{7\mu+3\sqrt{3\mu}}{3m}+\sqrt{\frac{3\mu}{m}\mathbb{P}_S(yf(x)<\theta)}\right]$$ 这里 $\mu=\frac{8}{\theta^2}\ln m\ln(2|\mathcal{H}|)+\ln\frac{2|\mathcal{H}|}{\delta}$。可以看到是O(log m/m)。可以证明这个界比Breiman和Schapire的界都一致更紧，并且用到的信息完全一样。

这就十分肯定的证明了考虑margin distribution的确是比minimum margin要好，更本质，更精确。

准确来说，通过一些变换，上面的界可以变换为考虑average margin和margin variance，那就是，同时考虑这两个属性比考虑minimum margin更本质。

Shivaswamy和Jebara在2011也已经给出了同时最大化average margin和最小化margin variance的算法，结果也是十分完美。

SVM

传统的SVM模型是通过最大化minimum margin来进行优化收敛的。基于上面的研究，我们可以看到用average margin和margin variance来优化SVM理论上模型测试误差会比传统的要好。

Large margin distribution machine | Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining

Zhang和周教授在2014年也发表了这篇论文肯定了相关的优化。