强化学习

多臂老虎机

马尔可夫决策过程与贝尔曼方程

Q-Learning

函数近似

DQN

AlphaGo

PPO

扩散策略

基于朱军老师的ppt

强化学习基础

强化学习可以看作是模型通过与环境的交互，最大化（长期）收益。将环境换为标签可以看到强化学习变为了有监督学习，而将有监督学习的数据一个个投喂给模型，用标签判断收益，也可以看作是强化学习。

此外，强化学习可以分为有无对环境建模：

• Model-based（有模型）强化学习：

  • 定义：智能体会尝试学习或使用一个“环境模型”。这个模型可以预测：如果在当前状态 \(s\) 采取动作 \(a\)，下一个状态 \(s'\) 会是什么，以及会获得多少奖励 \(r\)。这通常被建模为状态转移概率 \(p(s' | s, a)\)。

  • 核心功能——规划（Planning）：因为有了模型，智能体可以在实际行动之前，在脑海中进行“模拟”。它通过考虑未来的可能性来决定当下的最佳动作。

• Model-free（无模型）强化学习：

  • 定义：智能体不尝试理解环境运行的底层逻辑，而是完全通过试错（Trial-and-Error）来学习。

  • 特点：它直接通过经验来学习哪些动作能带来高回报，而不去预测下一个状态的具体样子。目前的许多深度强化学习研究主要集中在这一类方法上。

也可以分为同策略和异策略：

• On-policy（同策略）：智能体只学习它当前正在执行的那个策略。也就是说，它一边玩，一边用刚才玩出来的数据来改进自己。

• Off-policy（异策略）：智能体可以学习与当前执行策略不同的策略。这意味着它可以观察别人的行为来学习，或者利用很久以前的旧数据进行学习。

此外，学习方式正如开始对有监督学习的讨论，可以分为离线和在线：

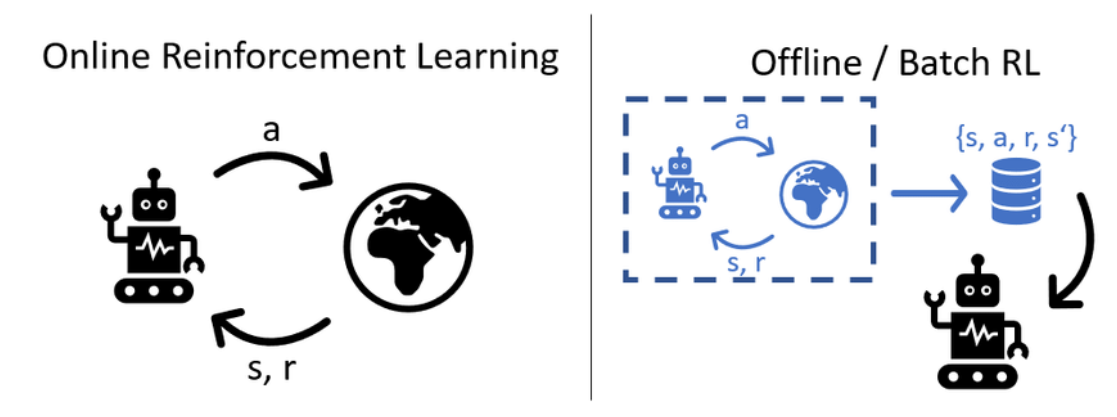
Online RL（左图）：智能体处于一个实时的循环中。它执行动作 \(a\) 到环境中，环境反馈状态 \(s\) 和奖励 \(r\)，智能体立即根据这些反馈进行学习并改进。

Offline / Batch RL（右图）：智能体不直接与环境交互。它面前有一个预先收集好的数据集（包含大量的 \(\{s, a, r, s'\}\) 轨迹）。智能体就像看书学习一样，从这些历史数据中挖掘最优策略，而不产生新的实时交互。

下面的多臂老虎机是无模型强化学习。

多臂老虎机 (Multi-armed Bandit)

背景

假设老虎机有很多扳手，每个扳手的期望回报不一样，但是玩家无法知道具体的期望回报，只能通过按下扳手后得到的观测值进行预估。

由于老虎机的回报不是确定的，最大化回报的最简单的想法之一就是所有扳手按足够多的次数，基于大数定理让平均值近似期望回报，然后选择期望回报最多的一致按下。

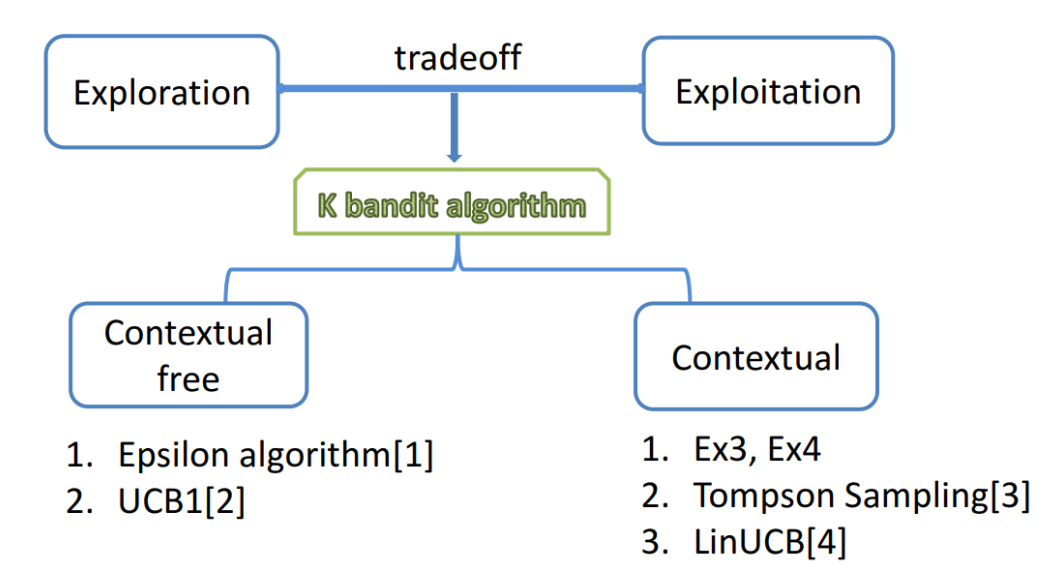
但可以看到，前面花费了很多次数用来按期望低的哪些扳手，这就是探索（exploration）与利用（exploitation）：为了找出回报最好的扳手，必须要先花费次数探索探索，探索过程中势必要因为按下非最好回报的扳手而花费更多。所以能平衡这两者至关重要。

利用 (Exploitation)：基于历史数据，做目前看来最好的决定。缺点：如果估计是错的，可能永远陷入局部最优。

探索 (Exploration)：去尝试那些未知的领域。缺点：可能会试到很差的选择，降低短期收益。

对于搜索引擎来说（虽然都用 ai 搜索引擎用的不多了），每一个广告位就像一个老虎机，用户“点击”就是“赢钱”，用户“忽略”就是“输钱”。平台需要通过算法决定展示哪个广告，以最大化点击率（CTR）。

定义

设置：\(K\) 个选项，每个选项 \(a\) 对应一个未知分布 \(P_a\)（均值为 \(\mu_a\)）。

流程：游戏进行 \(T\) 轮。在每一轮 \(t\)，我们要选择一个摇臂 \(j\)。

反馈：我们会得到一个从分布 \(P_j\) 中采样的随机回报 \(X_t\)。

为了评价选择如何，引入悔恨（regret）：

考虑最好的选项均值 \(\mu^* = \max\{\mu_a\}\)，瞬时（instantaneous）悔恨为 \(r_t = \mu^* - \mu_{a_t}\)，总悔恨为 \(R_T = \sum r_t\)。

于是，这个模型的基本目标就是让平均悔恨趋于 0：\(\frac{R_T}{T} \rightarrow 0\)。 也就是，让选择的选项收敛到 \(\mu^*\)。

Epsilon-Greedy Algorithm

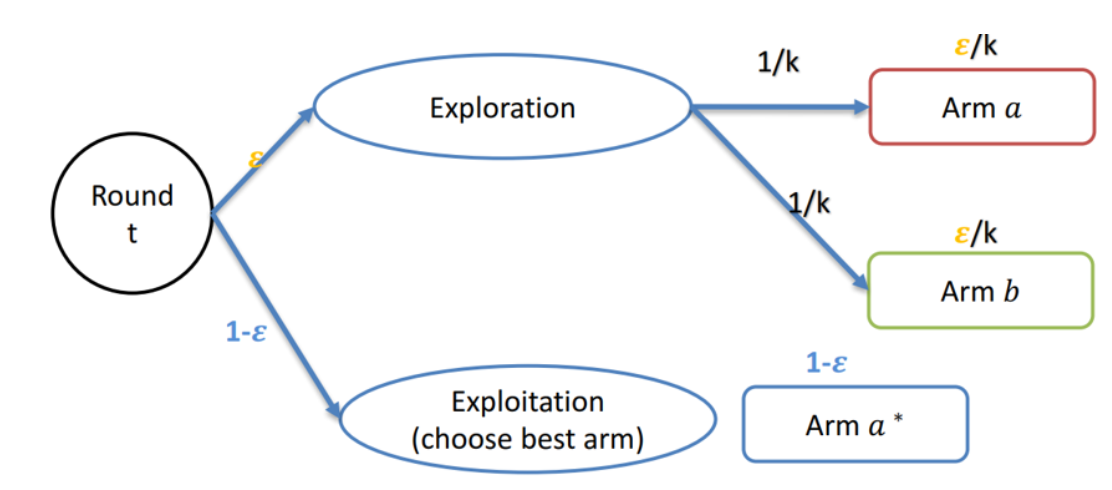
每次决策的时候，以 \(1-\epsilon\) 的概率：利用，选目前平均分最高的那个摇臂（Arm \(a^*\)）。以 \(\epsilon\) 的概率：探索，闭着眼睛随机选一个。

只要 \(\epsilon_t = O(1/t)\)，可以证明 regret 可以控制在 \(O(K \log T)\)，平均 regret 趋于 0。

虽然理论确实成立，但可以看到十分简单粗暴，\(\epsilon\) 探索的时候所有其他选项都是一致的，但通过先验信息我们可以完全不选某些选项，减少浪费。

UCB (Upper Confidence Bound)

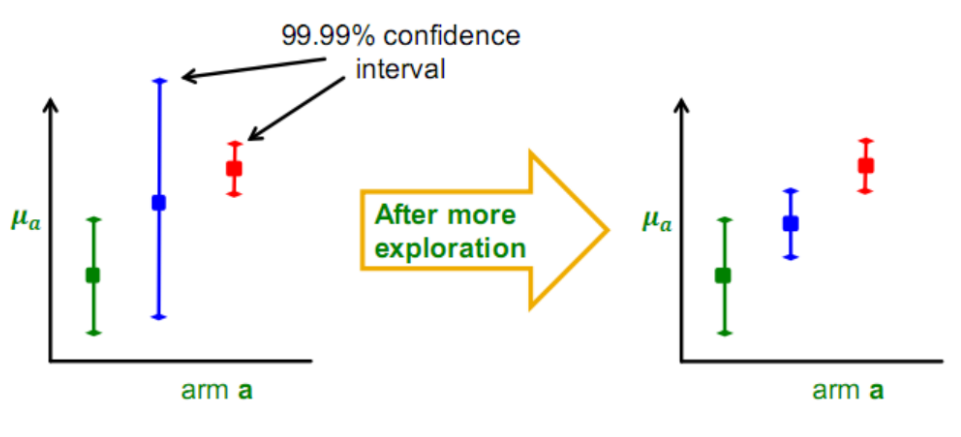
引入置信区间的思想，随着尝试次数增加，估计的均值 \(\mu_a\) 的置信区间会变窄（越来越确定）。尝试越少，区间越宽，意味着“潜力”越大。

于是如上图，可以在做决定时，总是假设每个摇臂都能达到它置信区间的上界 (Upper Bound)。如果一个摇臂虽然平均分低，但因为它很久没被试过，置信区间很宽，上界很高，依然选它。

更具体的，每次选择的时候计算所有选项的 UCB： \[ UCB(a) = \hat{\mu}_a + \alpha \sqrt{\frac{2 \ln t}{m_a}} \] 其中第一项 \(\hat{\mu}_a\) 是利用（Exploitation）；第二项是探索（Exploration），分母 \(m_a\) (该摇臂尝试次数) 越小，这一项越大，就会被优先选择。这保证了每个摇臂最终都会被尝试无穷多次，但好的摇臂会被尝试得更多。

可以证明 regret 是 \(O(K \ln T)\)，与 Epsilon-Greedy 相比无需控制 \(\epsilon\)，理论更好。

Thompson Sampling (贝叶斯方法)

从贝叶斯视角来看，与其对于每个选项维护一个具体的数值，不如维护对每个摇臂获胜概率的信念 (Belief/Distribution)。

每次决策时，从每个摇臂的分布里采样一个值 \(X\)，选择值最大的选项按下，用按下后的观测值更新此选项的后验分布。

和二元 NB 用 Beta 作为先验分布一样（共轭）。

每个摇臂维护两个数：成功次数 \(S_i\) 和失败次数 \(F_i\)。然后每轮从 \(Beta(S_i+1, F_i+1)\) 中采样。从 Beta 分布的角度来看，如果一个摇臂试得少，它的分布就很“扁平”（方差大），采样出来的值这就可能很高（探索）；如果试得多且好，分布就集中在 1 附近（利用）。

可以证明，Regret Bound 接近最优。

马尔可夫决策过程 (MDP) 与贝尔曼方程

前面假设了所有扳手不管什么状态按下相同扳手的期望回报都是一致的 (没有状态，stateless)，但很多情况如下棋，每一个动作 (Action) 都会影响环境的状态转移 (State Transition)。

为此，引入马尔可夫决策过程（Markov Decision Process）。马尔可夫决策过程由一个五元组 \(\mathcal{M} = \langle \mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma \rangle\) 构成：

1. \(\mathcal{S}\) (State space)：状态空间，所有可能情况的集合（比如棋盘上所有棋子的位置）。
2. \(\mathcal{A}\) (Action space)：动作空间，Agent 能做的事情（比如上下左右移动）。
3. \(\mathcal{P}\) (Transition Probability)：状态转移概率。\(P(s'|s, a)\) 表示在状态 \(s\) 做动作 \(a\) 后，转移到状态 \(s'\) 的概率。这代表了环境的动力学 (Dynamics)。
4. \(\mathcal{R}\) (Reward Function)：奖励函数 \(R(s, a)\)。做动作后环境给的反馈。
5. \(\gamma\) (Discount Factor)：折扣因子 \(\gamma \in [0, 1]\)。

马尔科夫性假设了当前状态仅基于前一状态： \[P(S_{t+1} | S_t, A_t, S_{t-1}, A_{t-1}, \dots) = P(S_{t+1} | S_t, A_t)\]。

于是，考虑确定性策略 \(a=\pi(s), \pi: \mathcal{S}\to \mathcal{A}\) 或随机策略 \(a \sim \pi(\cdot | s), \pi:\mathcal{S}\to\Delta(\mathcal{A})\)（这里 \(\Delta (\mathcal{A})\) 是 \(\mathcal{A}\) 分布的集合） 的模型，其通过选择最优 \(\pi\) 来最大化长期奖励： \[ \pi^* \in \arg \max_\pi \mathbb{E} \left[ \sum_{t=1}^\infty \gamma^{t-1} r_t | \pi \right] \] 这里引入 \(\gamma\) 来削弱后面状态的权重。

---

更具体的，定义回报为序列未来的加权（\(\gamma\)）奖励： \[ G_t = R_{t+1} + \gamma R_{t+2} + \gamma^2 R_{t+3} + \dots = \sum_{k=0}^{\infty} \gamma^k R_{t+k+1} \] 定义价值函数 \(V^\pi(s)\) 为状态 \(s\) 基于策略 \(\pi\) 的期望回报： \[ V^\pi(s) = \mathbb{E}_\pi [G_t | S_t = s] \] 定义动作价值函数 \(Q^\pi(s, a)\) 为基于策略 \(\pi\) 与状态 \(s\)，动作 \(a\) 的期望回报： \[ V^\pi(s) = \sum_{a \in \mathcal{A}} \pi(a|s) Q^\pi(s, a) \] 然后，贝尔曼指出最优决策具有递归性，即整体的最优依赖于局部子问题的最优。也就是，贝尔曼预期方程为： \[ V^\pi(s) = \sum_{a} \pi(a|s) \sum_{s'} P(s'|s, a) [ R(s,a) + \gamma V^\pi(s') ] \] 为了让策略 \(\pi\) 最优，可以让价值函数最大化：\(V^*(s) = \max_{\pi} V^\pi(s)\)。

于是贝尔曼最优方程就为（不用考虑 \(\pi\)）： \[ V^*(s) = \max_{a} \sum_{s'} P(s'|s, a) [ R(s,a) + \gamma V^*(s') ] \]

最短路径

考虑更具体的环境。

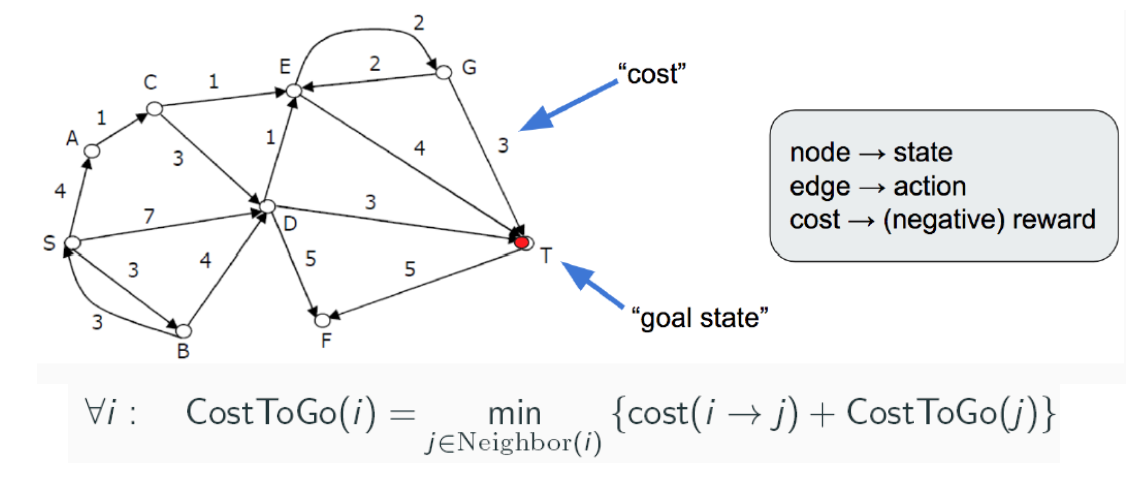
对于上图每个节点（状态），可以递归的定义负奖励（花费）为其到目标节点的最低花费。

于是，可以定义价值函数和动作价值函数： \[ V^*(s) = \max_{a \in \mathcal{A}} \{ R(s, a) + \gamma \mathbb{E}_{s' \sim P(\cdot|s,a)} [V^*(s')] \} \]

\[ Q^*(s, a) = R(s, a) + \gamma \mathbb{E}_{s' \sim P(\cdot|s,a)} \left[ \max_{a' \in \mathcal{A}} Q^*(s', a') \right] \]

贝尔曼算子

为了分析 \(Q^*\)，引入贝尔曼算子 \(\mathcal{B}\) 将 \(Q\) 映射到 \(\mathcal{B}Q\)： \[ \mathcal{B}Q(s, a) := R(s, a) + \gamma \mathbb{E}_{s' \sim P(\cdot|s,a)} [\max_{a'} Q(s', a')] \] 这表示，在状态 \(s\) 采取动作 \(a\) 的值等于即时奖励 \(R\) 加上折扣因子 \(\gamma\) 乘以下一个状态 \(s'\) 中所有可能动作的最大预期价值。

对于某个固定策略 \(\pi\)，有： \[ \mathcal{B}^\pi Q(s, a) := R(s, a) + \gamma \mathbb{E}_{s' \sim P(\cdot|s,a)} [Q(s', \pi(s'))] \] 也就是，对于固定 \(\pi\)，下一个状态 \(s'\) 动作是确定的（即 \(\pi(s')\)），因此不需要取最大值 \(\max\)。

现在解释为什么需要引入 \(\mathcal{B}\)。

在数学上，如果一个操作施加在某个函数上，结果仍然是该函数本身（即 \(f = \mathcal{B}f\)），则称该函数为该算子的不动点。可以看到，最优 \(Q\) 函数 (\(Q^*\)) 是算子 \(\mathcal{B}\) 的不动点，即 \(Q^* = \mathcal{B}Q^*\)。

并且，\(\mathcal{B}\) 有以下性质：

• 最优策略关联： 一旦得到了 \(Q^*\)，就可以直接推导出最优策略 \(\pi^*\)。更具体的，在每个状态下，选择能让 \(Q^*\) 达到最大值的动作即可（贪婪选择）。
• 单调性 (Monotonicity)： 如果函数 \(Q_1\) 在所有点都大于等于 \(Q_2\)，那么经过算子转换后的 \(\mathcal{B}Q_1\) 也一定大于等于 \(\mathcal{B}Q_2\)。这保证了更新过程的稳定性。
• 收敛性 (Contraction)： \(\mathcal{B}\) 是一个收缩映射。这意味着无论从什么样的初始 \(Q\) 函数开始，反复应用 \(\mathcal{B}\) 算子，函数之间的差距都会不断缩小，最终趋向于同一个值。
• 唯一性： 因为它是收缩映射，根据巴拿赫不动点定理，它的不动点 \(Q^*\) 不仅存在，而且是唯一的。

寻找最优策略

值迭代 (Value Iteration, VI)

值迭代直接在价值函数空间（\(Q\)）进行操作，不显式地维护一个策略，直到最后才提取策略。

基于 \(\mathcal{B}\)，可以设置以下算法得到 \(Q^*\)：

• 随机初始化 \(Q_0\)（如 \(Q_0\equiv 0\)）
• 对于 \(k=1,2,...\) 直到收敛，更新：\(Q_k\gets \mathcal{B}Q_{k-1}\)

由于收缩性质，算法以指数级速度收敛到 \(Q^*\)。

策略迭代 (Policy Iteration, PI)

策略迭代是一个在“策略空间”进行搜索的过程，通过不断切换更好的策略来达到最优：

• 随机初始化策略 \(\pi_0:\mathcal{S}\to\mathcal{A}\)
• 对 \(k=0,1,2,...\)：
  • 评估策略（policy evaluation）：计算当前策略 \(\pi_k\) 的长期价值 \(Q_k\)。更具体的，求解不动点（线性方程组）\(\mathcal{B}^{\pi_k} Q = Q\)，或者说，对于所有 \(s,a\)，求解 \(Q_k(s,a)=R(s,a)+\gamma\sum_{s'} P(s'|s,a)Q_k(s',\pi_k(s'))\)
  • 改进策略（policy improvement）：基于算出的 \(Q_k\)，将策略更新为最优：\(\pi_{k+1}(s) \leftarrow \arg \max_a Q_k(s, a)\)

整体可以看作是 \(\pi\) 对所有状态 \(s\) 同步进行局部优化，直到其对于所有状态都为最优。

可以证明，上述 \(\pi_{k+1}\) 更新要么严格变好，要么已经是最优。

VI 和 PI 的区别

特性	值迭代 (Value Iteration)	策略迭代 (Policy Iteration)
操作空间	价值函数空间 (\(Q\)-value space)	策略空间 (Policy space)
收敛性质	渐进收敛 (Asymptotic)，无限趋近 \(Q^*\)	有限时间内收敛 (Finite-time)，因为策略数量有限
迭代逻辑	\(Q_0 \to Q_1 \to Q_2 \dots \to Q^*\)	\(\pi_0 \xrightarrow{Q_0} \pi_1 \xrightarrow{Q_1} \dots \xrightarrow{Q_{K-1}} \pi_K = \pi^*\)
搜索方式	通过价值函数的逼近来间接找最优	类似于在策略空间进行“爬山算法” (Hill-climbing)

无模型学习：Q-Learning

上述过程都假定了奖励 \(R\) 与转移概率 \(P\) 都是已知的。对于一个未知环境可以用 Q-Learning。

考虑 \[ Q_k(s,a)=R(s,a)+\gamma\sum_{s'} P(s'|s,a)Q_k(s',\pi_k(s')) \] 假设 \(R\) 和 \(P\) 未知，那么我们可以通过已有数据 \(\mathcal{D} = (s_1, a_1, r_1, s_2, a_2, r_2, \dots)\) 替代、近似。

也就是，我们的目标是让 \(Q(s_t, a_t)\) 去逼近 \(r_t + \gamma \max_{a'} Q(s_{t+1}, a')\)。

于是，Q-Learning 通过以下更新学习 \(Q\)： \[ Q(s_t, a_t) \leftarrow Q(s_t, a_t) + \alpha_t \underbrace{(r_t + \gamma \max_{a'} Q(s_{t+1}, a') - Q(s_t, a_t))}_{\text{TD Error (时间差分误差)}} \] 这里 \(\alpha_t\in(0,1)\) 是学习率。这种方法不需要正确答案（\(R, P\)），而是自己利用对未来的估计（下一时刻的 \(Q\)）来更新现在的估计，想法类似于神经网络的权重更新。

可以看到，Q-learning 的更新是局部的（Local），每次只改一个 \((s, a)\) 的值。

Stochastic Approximation theory （随机近似理论）指出在满足以下条件时，Q-learning 几乎必然 (Almost Surely) 收敛到最优解 \(Q^*\)：对于所有 \((s,a)\)

1. \(\sum \alpha_t \cdot\mathbb{I}\{s_t=s,a_t=a\}= \infty\)（步长足够大，能一直学）。
2. \(\sum \alpha_t^2 \cdot\mathbb{I}\{s_t=s,a_t=a\} < \infty\)（步长慢慢变小，最后能稳定）。

可以看到，所有的 \((s, a)\) 也都要被访问无穷多次。

多步时序差分

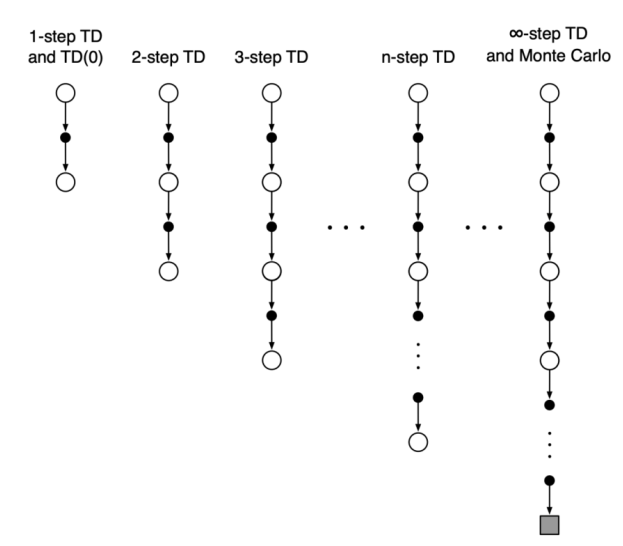
在 1-step 中，如果终点有一个巨大的奖励，这个信息每次更新只能往回传一个格子。如果有 100 个格子，模型至少要跑 100 次完整流程才能把奖励信息传到起点。而在 n-step 中，信息每步可以往回传 \(n\) 个格子，学习速度显著提升。

此外，1-step 高度依赖模型对下一个状态的“猜测”（即 \(Q(s')\)）。如果初始 Q 值很烂，学习就会很慢。n-step 引入了更多真实的奖励数据，减少了这种“用错误修正错误”的情况。

1-step：偏差高（依赖预估），方差低（每步都更新，很稳）。

n-step：步数越大，偏差越低（更多真实奖励），方差越高（受随机路径影响大）。

考虑 n-step 的回报 (Return，\(G_t^n\))：

• \(n=1\): \(R_{t+1} + \gamma v (S_{t+1})\) (标准 TD)
• \(n=2\): \(R_{t+1} + \gamma R_{t+2} + \gamma^2 v(S_{t+2})\)
• \(n=\infty\): \(R_{t+1} + \gamma R_{t+2} + \dots\) (MC)

TD 更新公式：\(v(S_t) \leftarrow v(S_t) + \alpha (G_t^n - v(S_t))\) 。

\(\epsilon\)-greedy 探索的 Q-Learning

可以看到，Q-Learning 的更新基于数据 \(\mathcal{D}\)，可以通过探索（exploration）获取。

用多臂老虎机介绍的 \(\epsilon\)-greedy 算法 Q-Learning 可变为：

输入：探索率 \(\epsilon\)，学习率 \(\alpha\)。

流程：

1. 对所有 \((s,a)\) 初始化 \(Q(s,a)\gets 0\)。
2. 观测初始状态 \(s_1\)。
3. 在每一步 \(t\)：
   • 决策：使用 \(\epsilon\)-greedy 策略选择动作 \(a_t\)（大部分时候选 \(Q\) 最大的，偶尔随机选）。
   • 执行：观察奖励 \(r_t\) 和新状态 \(s_{t+1}\)。
   • 学习：利用公式更新 \(Q(s_t, a_t)\)。

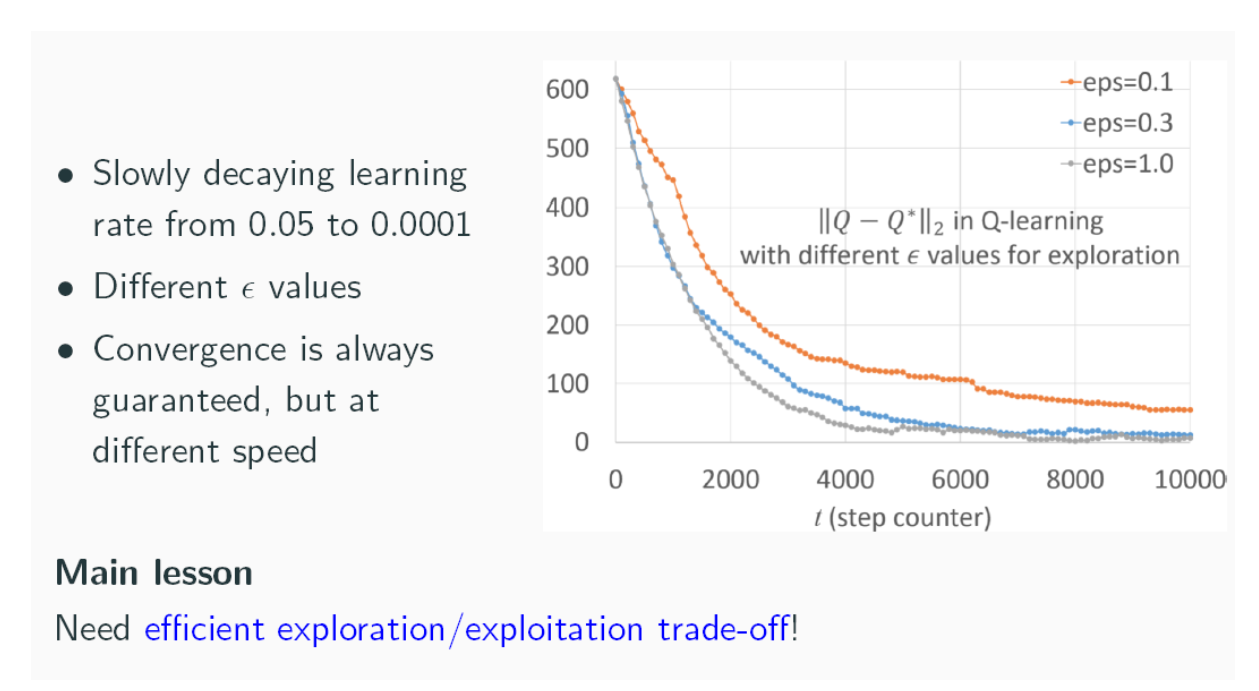
如前面讨论的，还是需要更好的平衡 exploration 和 exploitation。

基于 Bonus 探索的 Q-Learning（UCB）

与其随机选，可以给每个动作 \(a\) 一个 bonus \(B\)： \[ a_t = \arg\max_a \{ Q(s_t, a) + B(s_t, a) \} \] 如 bonus \(B\) 可以设计为 \(B(s, a) = \alpha / \sqrt{C(s, a)}\)，其中 \(C\) 是动作被选过的次数（这个情况的 bonus 思想就类似于 UCB）。

这种探索方法也被叫做有指导（guided）的探索。

其他探索方法

Boltzmann / Softmax Exploration：根据 Q 值的分布概率来选，Q 越大概率越大，而不是像 \(\epsilon\)-greedy 那样非黑即白。

Thompson Sampling：基于贝叶斯后验采样的探索。

Curiosity Driven (好奇心驱动)：通过预测误差等内在奖励（Intrinsic Reward）来驱动探索 。

深度强化学习

函数近似

之前的方法（如 Q-Table）都假设状态空间 \(S\) 和动作空间 \(A\) 是有限的，且可以精确计算。但如围棋的合法状态数是 \(2 \times 10^{170}\)，天文数字。

此外，在自动驾驶等问题中，状态和动作甚至是连续的（Continuous），无法通过 MDP 制表。

函数的表达方法：

• Tabular 制表、精确表示：因上面两个问题无法泛化
• Aggregation 聚合：把多个状态粗略地看成一个
• Linearly parametric approximation 线性参数估计：使用特征向量 \(\phi(s,a)\) 的线性组合来拟合 Q 值\[Q(s,a;\theta) = \theta^\top \phi(s,a)\]
• Nonlinear parametric approximation 非线性参数估计：用神经网络拟合
• Non-parametric representations 非参数化表示：核、决策树

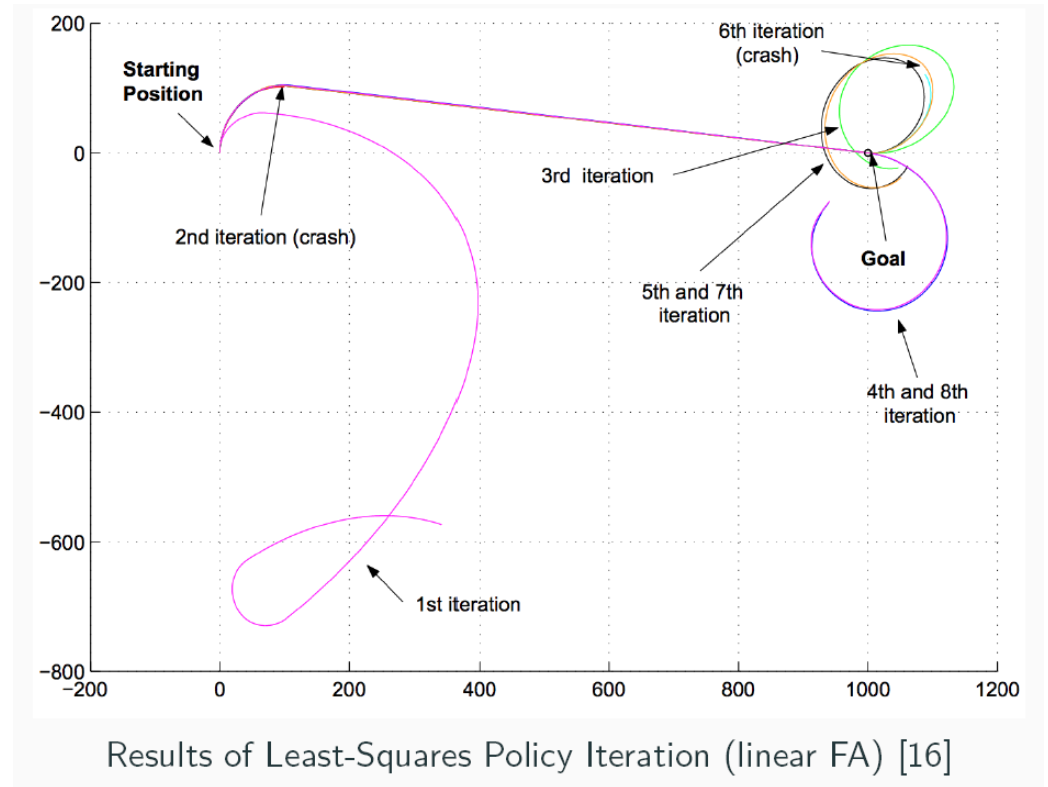
上图使用线性参数估计 Least-Squares Policy Iteration LSPI 学会了骑自行车。

更具体的，形式化骑自行车为：

• 状态 (\(s \in \mathbb{R}^6\))：包括车把角度 \(\theta\)、车身垂直角度 \(\omega\)、通往目标的角度 \(\psi\) 以及它们的导数（速度）。
• 动作 (\(a \in \mathbb{R}^2\))：施加在车把上的扭矩 \(\tau\) 和骑手的位移 \(\nu\) 。
• 线性参数：使用多项式基函数 (Polynomial basis) 构造特征 \[Q(s,a;\theta) = \theta_a^\top \phi(s)\]

但人工设计特征十分困难，可以用深度学习神经网络自动学习。

DQN (Deep Q-Network)

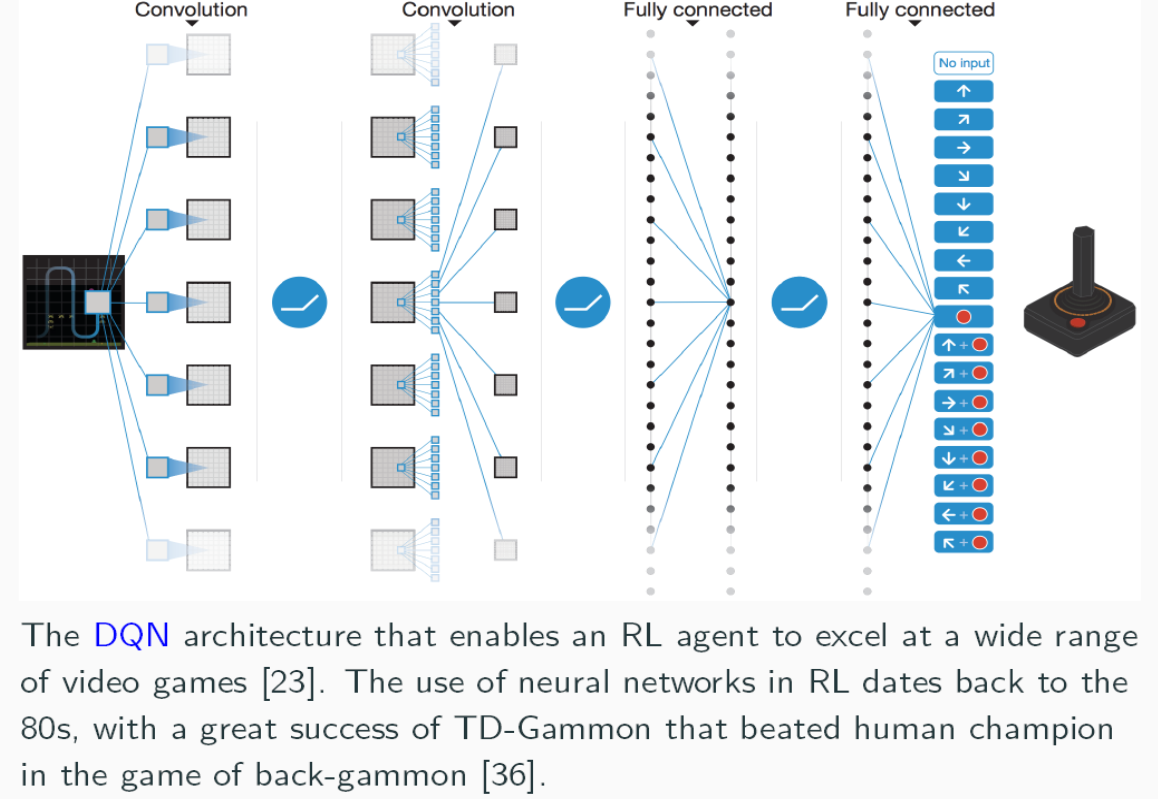
经典的 DQN 网络通过卷积和全连接层从原始像素输出 Q 值。

更具体的，相比之前 Q-Learning 的更新方法 \(Q \leftarrow Q + \alpha \cdot \text{TD\_Error}\) 直接更新 \(Q\)，可以利用梯度下降更新 \(\theta\)： \[ \theta \leftarrow \theta + \alpha_t \cdot \delta_t \cdot \nabla_\theta Q(s_t, a_t; \theta) \] 其中 \(\delta_t\) 是 TD Error：\(r_t + \gamma \max Q(s_{t+1}, \dots) - Q(s_t, \dots)\) 。

因对于线性 FA， \(Q(s,a;\theta)=\theta^\top\phi(s,a)\)，可以看到其对 \(\theta\) 的梯度就是特征向量 \(\phi(s,a)\)。

直接用神经网络结合 Q-learning 在实践中非常不稳定，可以通过技巧使其更加稳定：

• Experience Replay (经验回放)
• Two-network implementation (双网络/目标网络)

AlphaGo 与蒙特卡洛树搜索

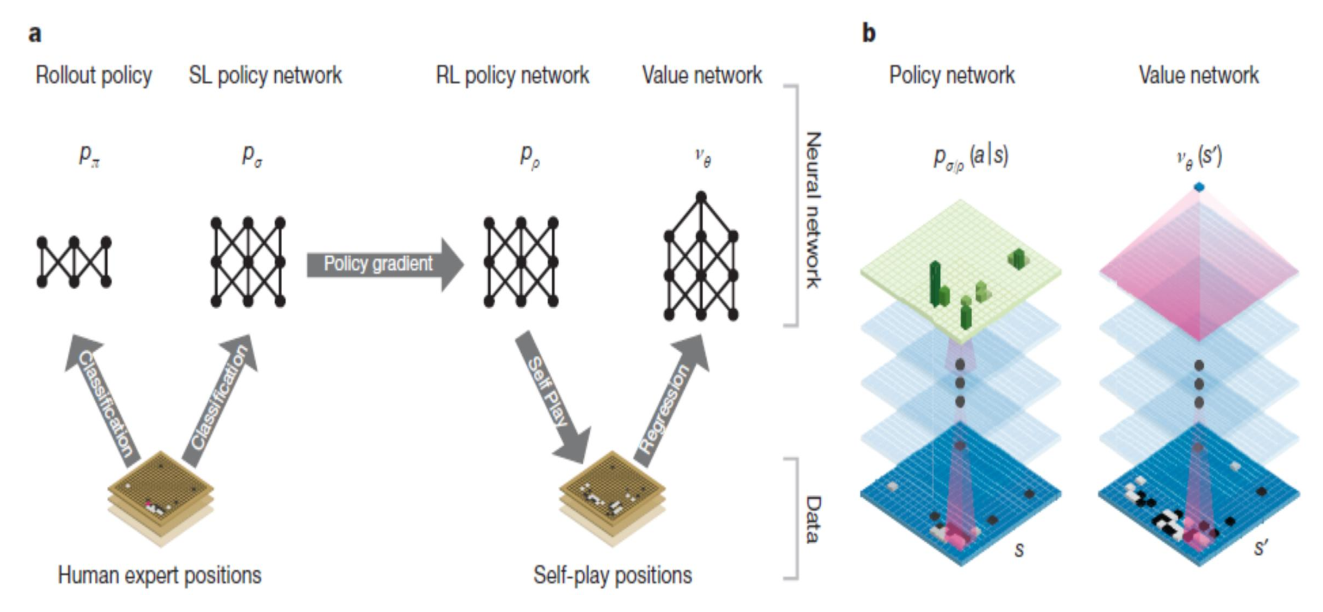
AlphaGo 分为四个模块：

1. Rollout Policy：快速走子策略 这是 AlphaGo 中最“简陋”但速度最快的部分，其目标是预测终局胜率。

技术细节：它不是深度神经网络，而是一个线性 Softmax 模型。它仅根据局部的棋盘特征（比如周围几格的棋子分布、是否叫吃等）进行决策。

性能特点：

极速：其决策速度大约是深度策略网络的 1500 倍（每次选择仅需 2 微秒）。

牺牲精度换规模：虽然它的落子准确率仅为 24% 左右（而深度网络超过 50%），但它能在一秒钟内模拟出成千上万局完整的对弈。

作用：在 MCTS 的“模拟（Simulation）”阶段，当搜索到达一个叶子节点时，AlphaGo 会利用 Rollout Policy 快速“盲下”到终局，根据最后的输赢结果给出一个粗略的胜率评分。

2. SL Policy Network：监督学习策略网络 这是 AlphaGo 的“基本功”，负责模仿人类高手的直觉。

训练方式：研究团队从 KGS 围棋服务器抓取了约 3000 万个职业棋手的落子位置。通过监督学习，让神经网络学习在特定盘面下人类最可能下在哪。

作用：

缩小搜索范围：围棋每一步有约 250 种选择，SL 网络能告诉模型“人类高手通常只看这 3-5 个点”，从而将搜索树的宽度大大压缩。

作为基石：它是后面强化学习（RL）网络的训练起点。

局限性：它只是在“模仿”，无法超越人类现有棋谱的逻辑。

3. RL Policy Network：强化学习策略网络 这是 AlphaGo 的“进阶进化”，负责突破人类极限。

训练方式：将 SL 网络复制一份，然后让模型开启“左右互搏（Self-play）”模式。通过数百万局的自我对弈，赢了的步骤加分，输了的扣分（Policy Gradient 算法）。

进化点：它不再追求“像人”，而只追求“赢”。这使得 AlphaGo 发现了一些人类棋手从未想过的奇招（如对阵李世石时的“神之一手”）。

核心贡献：RL 网络的主要产出并不是直接用来下棋，而是为了训练下一个组件——价值网络（Value Network）。

4. Value Network：价值网络 这是 AlphaGo 的“大局观”，负责评估盘面优劣。

功能：给它一个当前的棋盘图像，它会直接输出一个 0 到 1 之间的数字，代表当前黑棋或白棋的预计胜率。

训练难点：直接用棋谱训练会导致过拟合（因为同一局棋的相邻盘面极其相似）。AlphaGo 采用了 RL 网络的自我对弈数据，每局只取一个样本，确保了数据的多样性和客观性。

作用：在 MCTS 搜索中，它通过“看一眼”直接预测后续胜率，从而减少了搜索树的深度。它与 Rollout Policy 的模拟结果相结合，形成了一个极强且稳健的盘面评估函数。

总结：这四个组件如何协同工作？ 在 AlphaGo 思考下一步棋时（在线对弈过程）：

​ Selection（选择）：利用 SL 网络 的落子概率作为初始指引，优先搜索那些看起来更有可能的路径。

​ Evaluation（评估）：当搜索到某一个分支无法继续往下深入时，采用“双重保险”评估法：

​ 法 A：让 Value Network 扫视一眼，直接给出一个估值。

​ 法 B：让 Rollout Policy 快速模拟到终局，反馈一个结果。

Combination（综合）：将法 A 和法 B 的结果按一定权重（通常是 50/50）加权平均，作为这个分支的最终得分。

这种“直觉（Policy）+ 大局观（Value）+ 快速推演（Rollout）”的组合，构成了 AlphaGo 决策系统的底层逻辑。

MCTS（蒙特卡洛树搜索）与 Policy Network（策略网络）的关系，可以概括为“实战推演”与“直觉引导”的结合。在 AlphaGo 及其后续版本（如 AlphaZero）中，这种关系经历了从“辅助”到“深度融合”的演变。

以下是它们关系的详细分解：

1. 核心关系：引导搜索 vs. 被搜索精炼

• Policy Network 是“直觉” (Guide)：

  如果让 MCTS 盲目搜索，它会尝试棋盘上所有合法的落子点，这在围棋（搜索空间 \(10^{170}\)）中是不可行的。Policy Network 的作用是告诉 MCTS：“别乱看，优先看这几个最有前途的点。” 它大大缩小了搜索树的宽度。

• MCTS 是“思考” (Refiner)：

  Policy Network 给出的概率是基于当前盘面的瞬时判断。MCTS 通过上千次的模拟（推演未来），会对 Policy Network 的初始建议进行修正和精炼。最终落子的决定权在 MCTS 手中，而非 Policy Network。

---

2. 在 MCTS 搜索循环中的具体交互

在 MCTS 的四个阶段中，Policy Network 主要在“选择”和“扩展”阶段发挥作用：

A. 设定先验概率 (Prior Probability)

当 MCTS 扩展一个新节点时，它会调用 Policy Network。网络输出一个概率分布 \(P(s, a)\)，代表在当前局面 \(s\) 下，每一步棋 \(a\) 的价值。这个概率会被存储在树的边上，作为先验概率。

B. 影响 UCB 决策公式

在“选择”分支时，MCTS 使用一个变体公式（通常称为 PUCT）：

\[Score = Q(s, a) + C(P(s, a) \cdot \frac{\sqrt{N_{parent}}}{1 + N_{child}})\]

• \(Q\) (价值)：是之前搜索得到的平均胜率。
• \(P(s, a)\) (Policy 输出)：这个值越大，该分支被选中的概率就越高。
• 关系：在搜索初期，由于 \(Q\) 还没有参考价值，Policy Network (\(P\)) 主导了搜索方向；随着搜索次数增加，\(Q\) 的重要性提升，实战推演的结果开始纠正初始直觉。

---

3. 两种 Policy Network 的不同角色 (AlphaGo 早期版本)

在经典的 AlphaGo (Lee) 中，其实存在两个策略网络：

1. SL Policy (监督学习网络)：用于在 MCTS 搜索树内提供先验概率。它的精度高，但计算相对慢。
2. Rollout Policy (快速走子网络)：用于在 MCTS 树外的“仿真（Simulation）”阶段。它不属于深度网络，速度极快，负责在几微秒内直接下到终局，给 MCTS 提供一个粗略的胜负参考。

---

4. 进化：从“模仿者”到“自我老师” (AlphaZero 架构)

在更先进的 AlphaZero 中，MCTS 和 Policy Network 的关系变成了一种循环迭代的训练关系：

1. MCTS 产生更好的策略：对于一个局面 \(s\)，Policy Network 可能觉得 \(A\) 点胜率 40%，\(B\) 点 60%。但 MCTS 搜索 1600 次后发现，\(A\) 点最终胜率其实是 80%。此时，MCTS 生成的搜索分布 \(\pi\) 比原始的 Policy 网络 \(P\) 更强大。
2. MCTS 指导 Policy 学习：AlphaZero 会把 MCTS 的搜索结果 \(\pi\) 作为“标签”，回头去训练 Policy Network。
   • 目标：让神经网络的输出 \(P\) 越来越接近 MCTS 搜索后的结果 \(\pi\)。
3. 结果：神经网络通过不断“复盘” MCTS 的深度思考结果，变得越来越聪明，从而在下一次搜索时能提供更精准的引导。

---

总结

• Policy Network 是“眼”：负责在成千上万的选择中扫视，锁定几个目标。
• MCTS 是“脑”：负责针对这几个目标进行深度算力推演。
• 具体联系：Policy Network 初始化了搜索树的权重，而 MCTS 通过采样和评估不断更新这些权重。最终，AI 选择的是经过思考（MCTS）后的最佳路径，而不是看起来最美（Policy Network）的路径。

RL 总结

例子

考虑这个射击游戏例子：

1. 信息不完全：只能看到第一人称视角，不知道敌人在哪（部分可观测）。

   针对这种复杂环境，需要更复杂的模块设计。如感知 (Perception)、状态估计 (State Estimate)、规划 (Planner)、分层学习 (Hierarchical Learning)。

2. 3D 环境。为了应对庞大的动作空间，使用了“宏动作” (Macro actions)，也叫 Combo-Action。比如把 “Turn” + “Shoot” 组合成一个动作序列，而不是每一步都单独决策。

3. 稀疏奖励 (Sparse Reward)：只有游戏结束才知道输赢。

PPO

近端策略优化（Proximal Policy Optimization, PPO） 是一种在强化学习中广泛使用的策略梯度（Policy Gradient）*算法。其核心要点在于：通过引入*裁剪（Clipping）机制来限制策略更新的幅度，从而解决了传统算法中容易因更新步长过大而导致训练崩溃的问题。

PPO 兼顾了实现简单、采样效率高和易于调参的优点，是目前 OpenAI 等机构默认的首选算法。

---

PPO 核心原理与机制详细解析

1. 核心目标：信赖域更新

在强化学习中，策略更新步长是一个难题：

• 步长太小：训练速度极慢。

• 步长太大：新旧策略差异过大，可能导致性能断崖式下跌，且很难恢复。

  PPO 的设计灵感来自 TRPO（信任区域策略优化），但通过更简单的数学手段实现了类似的稳定性，确保新策略 \(\theta\) 不会偏离旧策略 \(\theta_{old}\) 太远。

2. 目标函数与裁剪机制（PPO-Clip）

这是 PPO 最具代表性的部分。其损失函数公式如下：

\[L^{CLIP}(\theta) = \hat{\mathbb{E}}_t \left[ \min(r_t(\theta) \hat{A}_t, \text{clip}(r_t(\theta), 1 - \epsilon, 1 + \epsilon) \hat{A}_t) \right]\]

• 概率比率 \(r_t(\theta)\)：表示动作在当前策略和旧策略下的概率比。
• 优势函数 \(\hat{A}_t\)：衡量当前动作比平均状态好多少。
• 裁剪过程：
  • 当 \(\hat{A}_t > 0\)（动作表现好）时，我们增加该动作概率，但 \(r_t(\theta)\) 被限制在 \(1+\epsilon\) 以内。
  • 当 \(\hat{A}_t < 0\)（动作表现差）时，我们减少该动作概率，但 \(r_t(\theta)\) 被限制在 \(1-\epsilon\) 以外。
• 作用：这种“去激励”过度更新的机制，保证了即使环境反馈波动剧烈，模型也能稳健前行。

3. 重要性采样（Importance Sampling）

PPO 属于同策略（On-policy）算法的改进版。它利用重要性采样技术，允许在单次迭代中使用同一批采样数据进行多次随机梯度下降（SGD）更新。

• 通过概率比率 \(r_t(\theta)\)，模型可以计算“如果我按照当前策略执行，得到这些奖励的概率是多少”，从而提高了数据的利用率。

4. Actor-Critic 架构

PPO 通常采用 Actor-Critic 结构运行：

• Actor（策略网络）：负责输出动作。其损失包含上述的 CLIP 损失。
• Critic（价值网络）：负责估计状态价值 \(V(s)\)。其损失通常是均方误差（MSE），用于减小价值估计与实际回报之间的差距。
• 熵正则化（Entropy Bonus）：在总损失中加入熵项，鼓励智能体保持一定的探索性，防止过早收敛到局部最优。

---

PPO 的主要流程

1. 数据收集：使用当前策略 \(\theta_{old}\) 在环境中运行 \(T\) 个时间步，收集状态、动作和奖励。
2. 计算优势：根据收集到的奖励和 Critic 的预测值，计算每个时间步的优势函数 \(\hat{A}_t\)（通常使用 GAE，即广义优势估计）。
3. 优化循环：
   • 在同一批数据上重复进行 \(K\) 个 Epoch 的训练。
   • 计算 CLIP 损失、价值损失和熵损失的总和。
   • 通过反向传播更新网络参数 \(\theta\)。
4. 同步参数：将更新后的参数设为新的 \(\theta_{old}\)，进入下一轮循环。

---

为什么 PPO 如此流行？

特性	说明
稳定性	裁剪机制有效防止了策略坍塌。
易用性	相比 TRPO 复杂的二阶导数计算（KLD 约束），PPO 仅需一阶导数。
通用性	无论是在连续控制（机器人）还是离散控制（游戏/LLM）中表现都非常出色。
RLHF 核心	在大语言模型的对齐阶段（RLHF），PPO 是目前最主流的微调算法。

扩散策略 (Diffusion Policies)

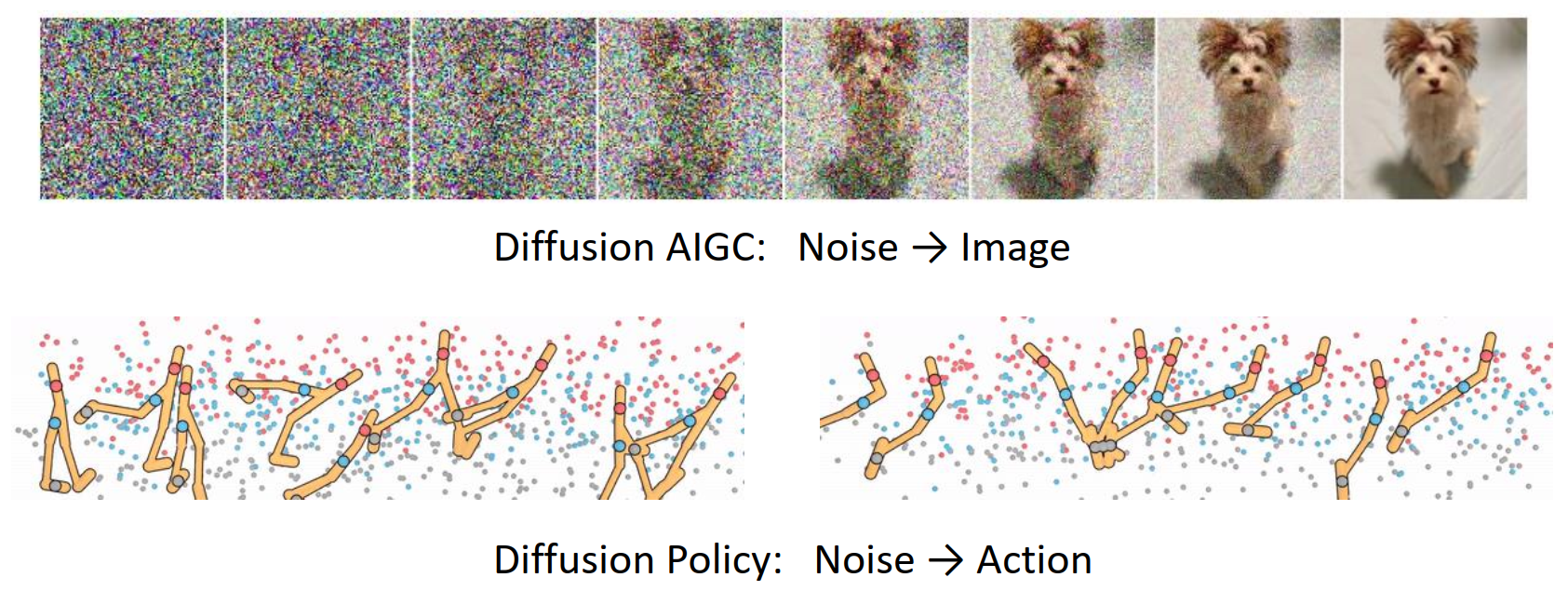
传统的图像生成扩散模型将噪音变为图片。

基于类似想法，扩散策略将噪音变为动作（序列）。

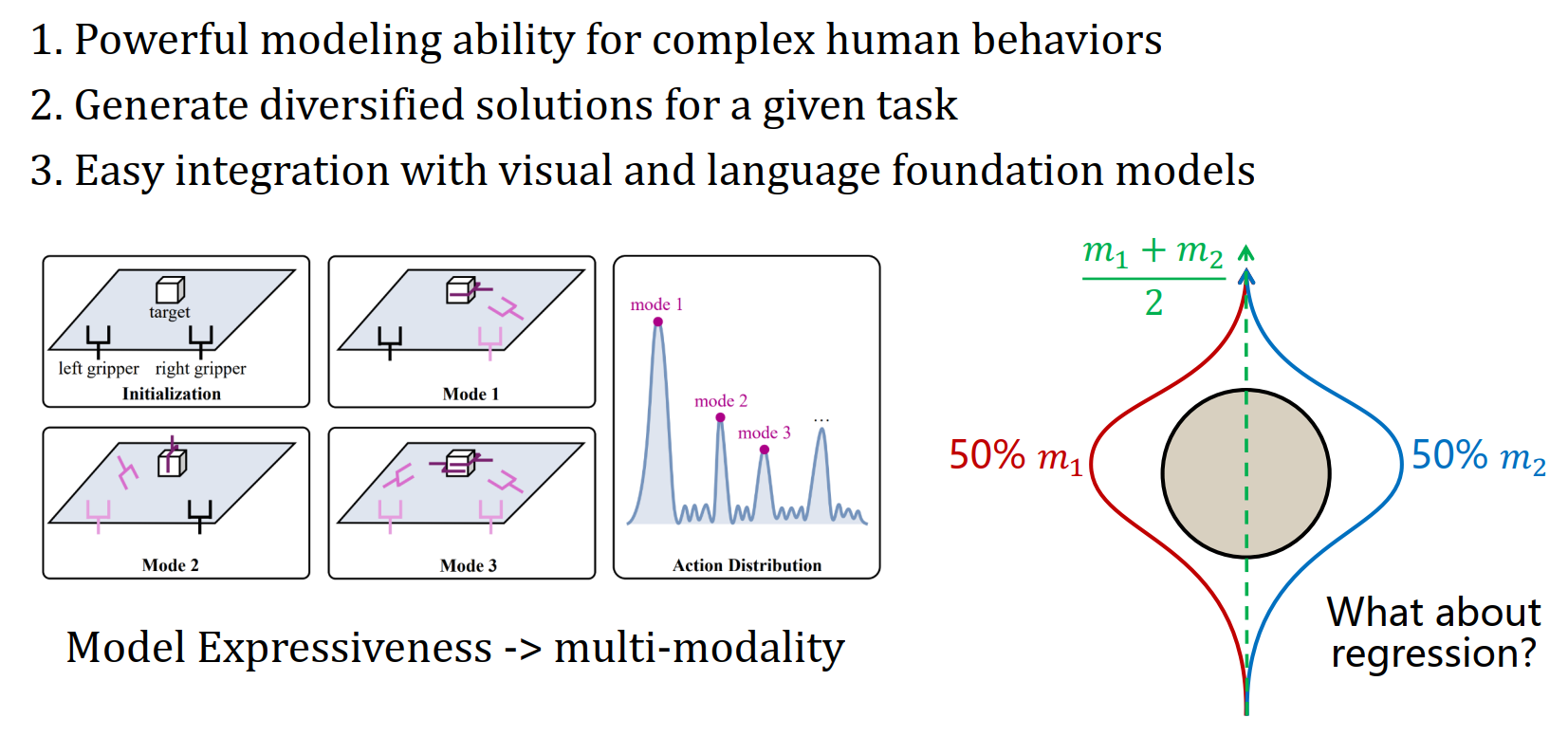
扩散模型引入的多样性与不确定性解决了三个问题： - 强大的建模能力：能够拟合复杂的、多模态的人类行为（比如抓杯子既可以从左边抓，也可以从右边抓，传统的高斯策略很难处理这种“多峰”分布）。 - 多样性 (Diversity)：对于同一个任务，能生成多种不同的解决方案。 - 兼容性 (Integration)：天然适合与视觉（Vision）和语言（Language）等基础模型结合 。

虽然好用，但扩散策略落地有三大痛点：

• 数据稀缺 (Data Scarcity)：机器人数据太少，导致泛化性差 \(\rightarrow\) 解决方案：RDT-1B。
• 推理太慢 (Low Frequency)：扩散模型需要几十步迭代去噪，导致控制频率只有 2-5Hz，无法实时反应 \(\rightarrow\) 解决方案：SRPO。
• 对齐困难 (Alignment)：难以计算似然度（Likelihood），导致无法像 LLM 那样方便地做 RLHF（人类反馈强化学习） \(\rightarrow\) 解决方案：EDA 。

RDT-1B

现有 VLA 模型的局限

目前的 VLA (Vision-Language-Action) 模型（如 RT-2）大多基于 Transformer 进行离散化预测或回归。

问题：

• 信息丢失：把连续动作强行离散化。
• 缺乏多样性：只能输出单一的确定性动作，丢失了行为的丰富性 。

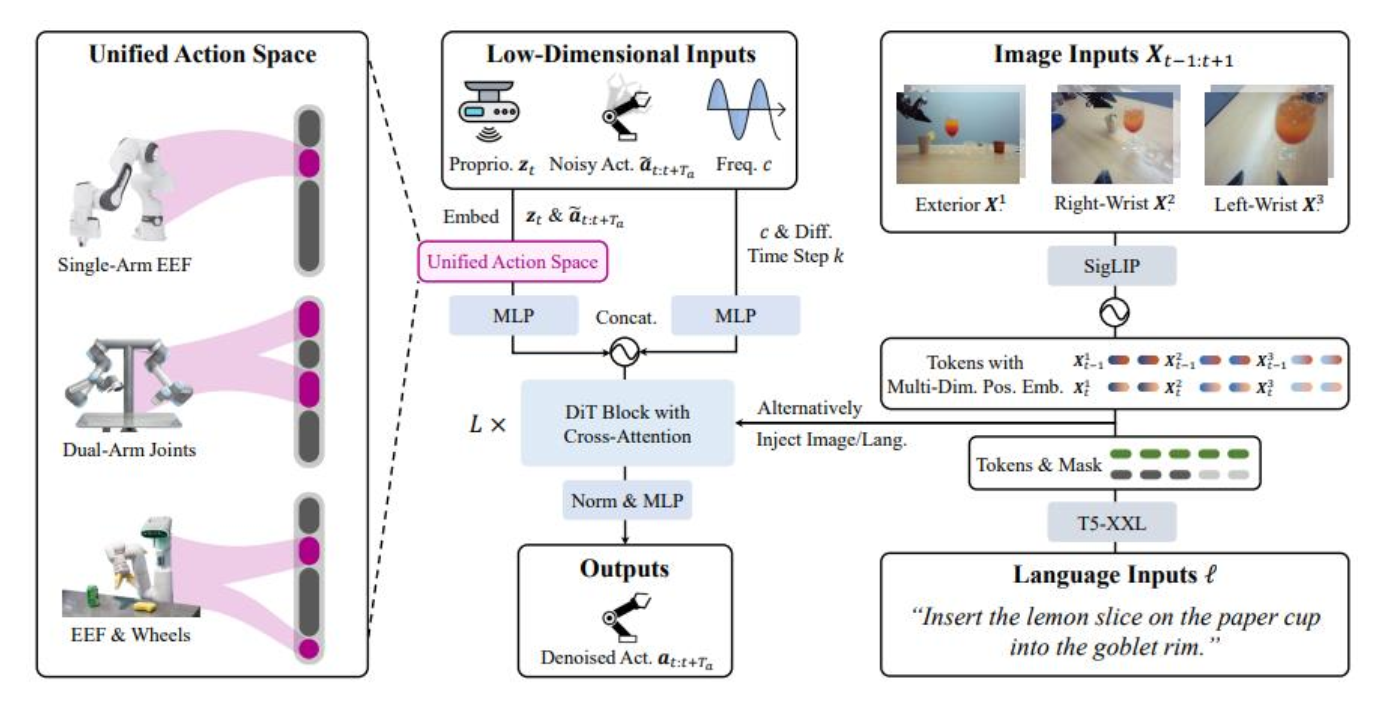
架构

核心架构：Diffusion Transformer (DiT)。

输入：图像（多视角）、本体感知信息（关节角度）、语言指令。

输出：去噪后的动作序列。

特点：支持异构动作空间（Heterogeneous action spaces），即不管是单臂、双臂还是带轮子的机器人，都能统一处理 。

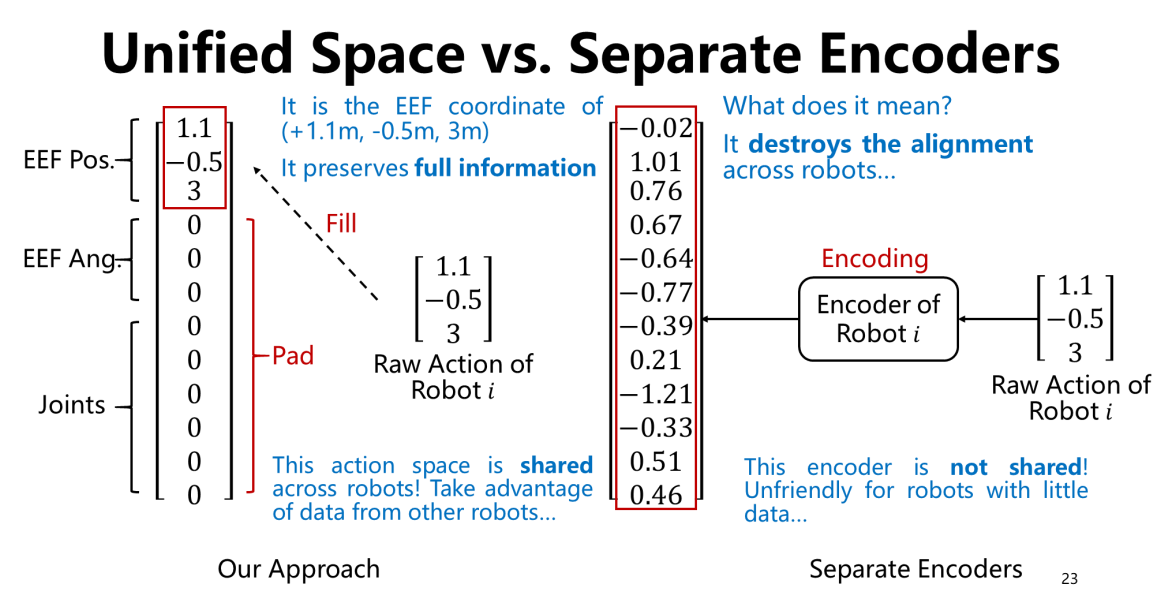
痛点：不同机器人的物理参数不一样（有的只有末端执行器 EEF，有的有 7 个关节）。

创新：设计了一个统一的动作编码空间。

• 保留信息：不像简单的 EEF 映射那样丢失关节信息。
• 共享编码器：让数据少的机器人也能借用数据多的机器人的知识 。

SRPO

核心矛盾

矛盾：机器人控制通常需要 50Hz 以上的频率，但标准扩散模型采样一次需要迭代几十步，频率只有 2-5Hz。

思路：能否从一个预训练好的扩散模型中，蒸馏 (Distill) 出一个确定性的策略网络，使得它只需要推理一次。

EDA

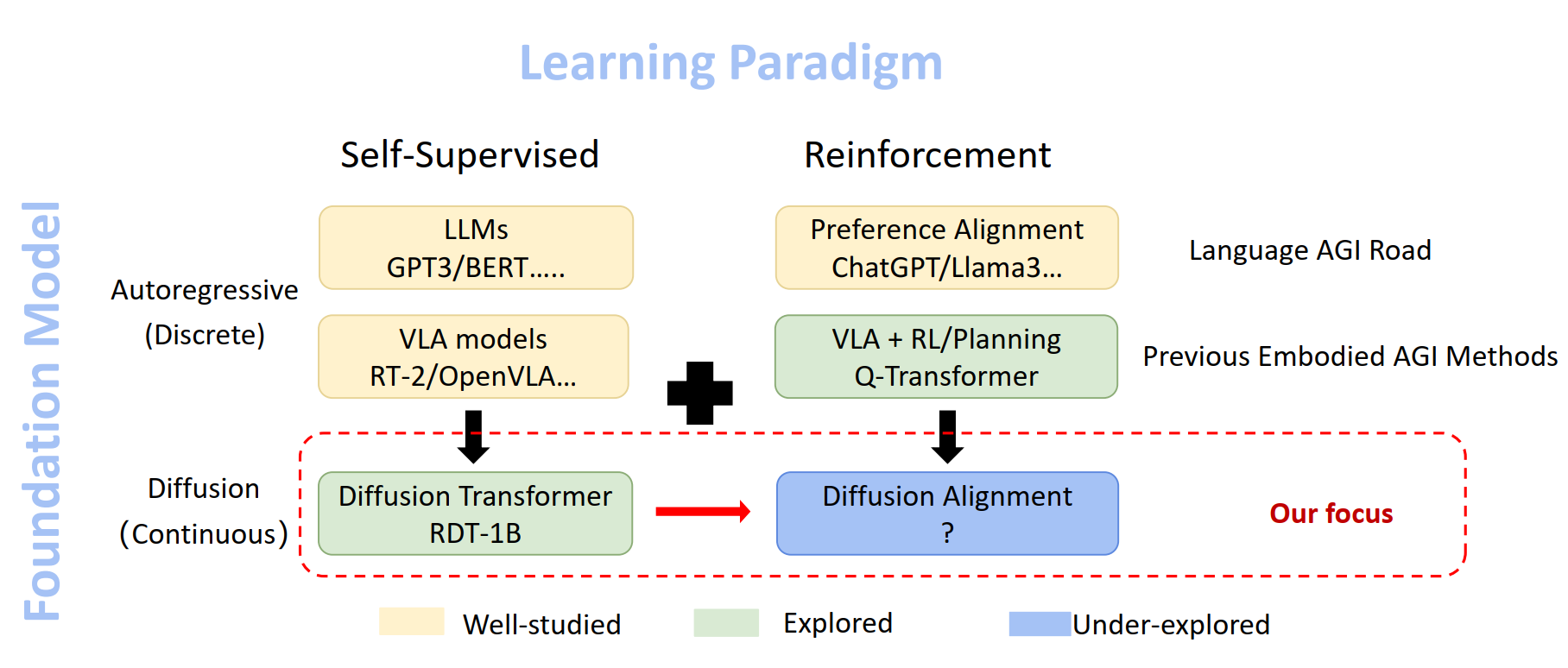
LLM：Pre-training (GPT) \(\rightarrow\) Alignment (ChatGPT/RLHF)。

Diffusion Policy：RDT-1B (Pre-training) \(\rightarrow\) ? (Alignment)。

什么是扩散对齐

SFT (Supervised Fine-tuning)：用行为数据让机器人学会“怎么做”。

RL (Alignment)：用奖励信号（Reward）让机器人学会“做得更好”或“适应新任务” 。

问题

难点：PPO 等主流 RL 算法需要计算策略的概率密度 \(\pi(a|s)\)（Likelihood）。

冲突：扩散模型是基于 Score Matching 的，它输出的是梯度（Gradient fields），而不是概率密度。算不出概率，就没法算 Importance Sampling Ratio，也就没法用 PPO。

EDA 解决方法

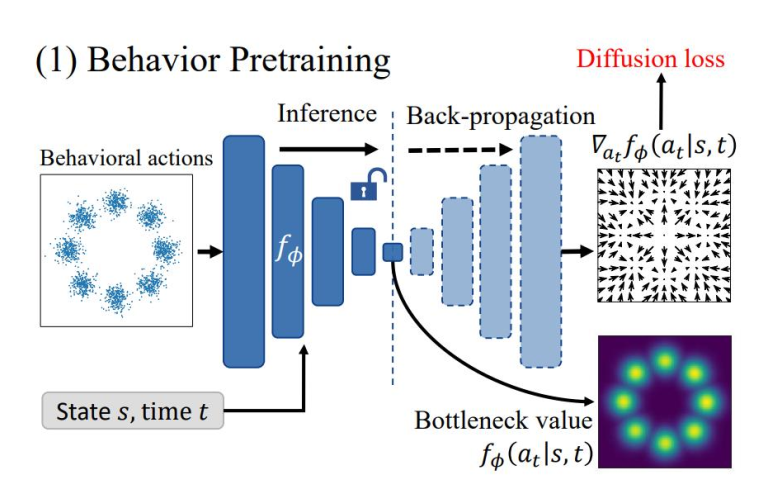
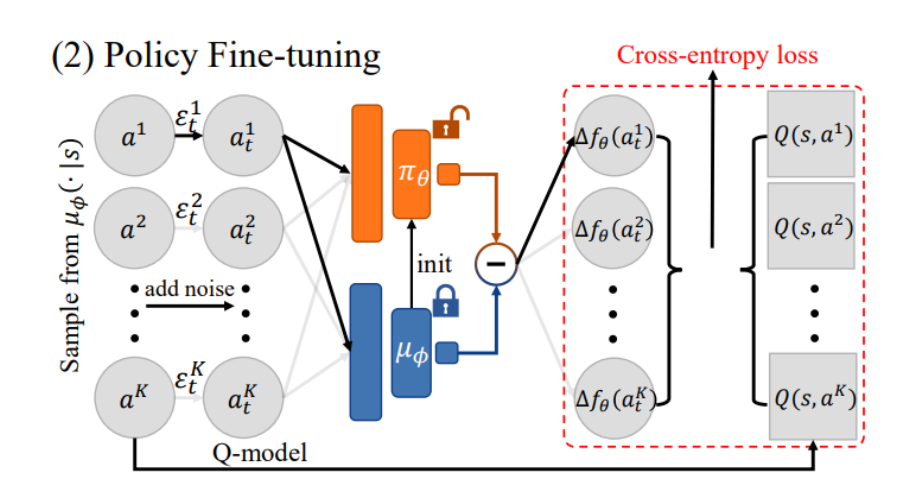
EDA 分为两个阶段：

1. 提出一种新的扩散建模技术，使其能够直接估计密度 (Direct Density Estimation)。
2. 利用第一阶段得到的密度估计能力，结合 Q-Learning 算出的优势函数 (Advantage)，对扩散策略进行高效微调。