SVM

二元分类任务可以看作是将输入（特征）空间分成两部分。

受AdaBoost启发的Margin Theory间隔理论 - alittlebear’s blog

从间隔理论的角度来看，SVM（支持向量机）的核心优化目标是最大化最小间隔。

（本页基于朱军老师的PPT）

线性支持向量机 Linear SVM

硬间隔SVM Primal Hard SVM

考虑用超平面（作为分类器）\(w^\top x+b=0\)分割输入空间（这里我们假设数据是完美线性可分的，不能有噪点），输入\(x_i\)距离超平面的距离为\(r = \frac{|w^T x_i + b|}{||w||}\)，将最近超平面的输入（距离为\(\rho /2\)）成称为支持向量（support vector），那么对于所有输入\(x_i\)：

\[y_i(w^T x_i + b) \ge \rho /2\]

等式成立当且仅当\(x_i\)是支持向量。将\(w\)和\(b\)缩小\(\rho/2\)后可以看到对于支持向量\(|w^T x_i + b|=1\)，得出\(r=\frac1{||w||}\)，也就是\(\rho=2r=\frac2{||w||}\)​​。

硬间隔SVM的缺点

可以看到这个SVM对于数据线性可分的需求太强烈了，为了避免这个假设，可以进行两种改进（一会考虑）：

1. 增加特征，增加输入维度来区分数据（容易过拟合，找到合适的也不容易）
2. 减缓约束条件（允许少量分类错误）

拉格朗日乘数法和对偶 Lagrange Multiplier and Dual

为了最大化\(\rho\)，我们最小化\(\frac12||w||^2\)，但有限制\(\forall i.y_i w^\top x_i\ge 1\)。

在数学上可以通过拉格朗日乘数法Lagrange Multiplier先将原始（primal）问题转换成等价的对偶（dual）问题。

原始问题：

\[\hat{\mathbf{w}} = \arg\min_{\mathbf{w}} \frac{1}{2} ||\mathbf{w}||^2\]

s.t. \[ y_i \mathbf{w}^\top \mathbf{x}_i \ge 1, \quad \forall i = 1, \dots, N\]

拉格朗日函数：

\[L(\mathbf{w}, \alpha) = \frac{1}{2} ||\mathbf{w}||^2 - \sum_{i=1}^N \alpha_i (y_i \mathbf{w}^\top \mathbf{x}_i - 1)\]

s.t. \[\alpha = (\alpha_1, \dots, \alpha_N)^\top \ge 0\]

可以看到，我们引入\(\alpha\)来合并原问题的优化函数和限制。

对\(L\)取\(w\)的偏导，得到最优\(w\)，代入进去再求最优\(\alpha\)：

\[\hat{\alpha} = \underset{\alpha\ge 0}{\text{argmax}} \left( \alpha^{\top}1 - \frac{1}{2}\alpha^{\top}YGY\alpha \right)\]

这里\(Y=diag(y_1,...,y_N), G_{ij}=x_i^\top x_j\) 是Gram矩阵。

可以看到对偶问题的\(x_i\)都转换成了\(G\)里面的\(x_i^\top x_j\)形式，一会介绍核函数\(K(x_i,x_j)\)的时候就知道为什么这样更便于计算了。

预测：

\[f(\mathbf{x};\hat{\mathbf{w}})=\mathrm{sign}\left(\hat{\mathbf{w}}^\top\mathbf{x}\right)=\mathrm{sign}\left(\sum_{i=1}^N\hat{\alpha}_iy_i\mathbf{x}_i^\top\mathbf{x}\right)\]

输出基于支持向量（参考下面KKT条件小节）对于输入的线性加权和。

计算对偶的优点

除了上面提到的核函数，计算对偶函数还有其他几个优点

1. 相比于原来问题，对偶问题的限制更加简单（\(\alpha\ge0\)）
2. 正如这篇论文介绍，存在很多快速的二次规划算法（quadratic programming algorithms）可以优化对偶问题，特别是在输入维度特别高的情况下。

软间隔SVM Primal Soft SVM

在硬间隔SVM，原始问题可以写成：

\[\hat{\mathbf{w}}=\arg\operatorname*{min}_{\mathbf{w}}\frac{\lambda}{2}\|\mathbf{w}\|^{2}+\sum_{i=1}^{N}\ell_{0-\infty}(y_{i}\mathbf{w}^{\top}\mathbf{x}_{i})\]

这里 \[\ell_{0-\infty}(b)=\begin{cases}\infty & b<0\\ 0 & b >0\end{cases}\]。

为了允许错误，尝试使用\[\ell_{0-1}(b)=\begin{cases}1 & b<0\\ 0 & b >0\end{cases}\] 来替代\(\ell_{0-\infty}(b)\)。

\(\ell_{o-1}\)的问题

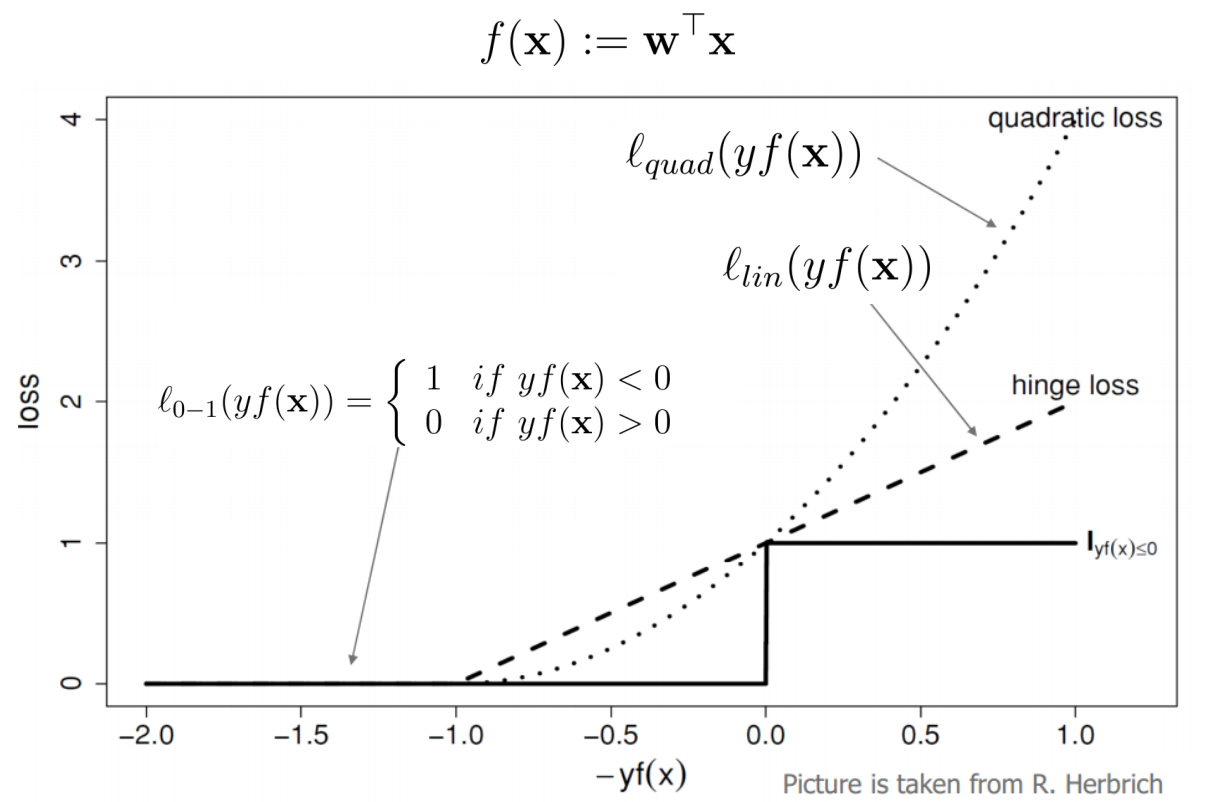
在机器学习我们都喜欢光滑（可导）的凸函数，

为此，在\(\ell_{o-1}\)的基础上考虑几个损失函数

• \(\ell_{lin}(yf(x))=\max(0,1-yf(x))\) 也被称为Hinge loss，可以看到是凸，但非光滑。

• \(\ell_{quad}(yf(x))=\max(0,1-yf(x))^2\)，凸并光滑。

• \[\ell_{Huber}(yf(x))=\begin{cases}1-yf(x) & yf(X)<0\\\max(0,1-yf(x))^2 & yf(X)\ge0\end{cases}\]，被称为Huber loss，凸但非平滑。不过可以看到，对于分类错误的点，\(\ell_{quad}\)把损失给平方了，这样噪声对于模型的影响太大了（影响\(w\)的更新），为了使模型更加鲁棒robust，对于分类错误的点Huber loss仅给予线性惩罚（虽然变得不光滑了，但可以像ReLU一样通过sub-gradient次梯度解决）。

\(\ell_{lin}\) Hinge Loss

用Hinge loss，可以将原问题写成

\[\hat{\mathbf{w}}=\arg\operatorname*{min}_{\mathbf{w}}\frac{\lambda}{2}\|\mathbf{w}\|^{2}+C\sum_{i=1}^{N}\xi_i\]

\[\xi_i:=\ell_{lin}(y_{i}\mathbf{w}^{\top}\mathbf{x}_{i}), C:=\frac1\lambda\]

s.t. \(y_{i}\mathbf{w}^{\top}\mathbf{x}_{i}\ge 1-\xi_i\)和\(\xi_i\ge0\)。

对应的拉格朗日函数就是：

\[L(\mathbf{w},\boldsymbol{\xi},\boldsymbol{\alpha},\boldsymbol{\beta})=\frac{1}{2}\|\mathbf{w}\|^{2}+C\sum_{i}\xi_{i}-\sum_{i}\alpha_{i}(y_{i}\mathbf{w}^{\top}\mathbf{x}_{i}-1+\xi_{i})-\sum_{i}\beta_{i}\xi_{i}\]

最后求解最优\(\alpha\)：

\[\hat{\alpha} = \underset{0\le\alpha\le C1}{\text{argmax}} \left( \alpha^{\top}1 - \frac{1}{2}\alpha^{\top}YGY\alpha \right)\]

可以看到和硬间隔SVM的\(\hat{\alpha}\)是完全一样的除了\(C1\)的限制。

为什么SVM叫SVM（KKT条件）

在凸优化问题，满足KKT条件的解一定是最优解（非凸情况不一定）。

对于硬间隔SVM的\(L(w,\alpha)\)，KKT条件（互补松弛条件Complementary Slackness）就是对于所有\(i\)，\[ \hat{\alpha}_{i}(y_{i}\hat{w}^{\top}x_{i}-1)=0\]，也就是，要么\(\hat{\alpha}_{i}=0\)要么\(y_{i}\hat{w}^{\top}x_{i}=1\)，i.e.，是支持向量。

可以看到，对于最优解，影响参数的只有支持向量，这也是为什么模型叫支持向量机。

对于软间隔SVM，分类错误的向量也属于支持向量。

因为支持向量的数量不多，\(\hat{\alpha}_{i}=0\)占\(i\)的绝大多数。也就是，只有几个对偶变量\(\alpha_i\ne0\)，这个现象叫做Dual sparsity（对偶稀疏化），从这个角度来看SVM本质上就是一种稀疏表示sparse representation

多类扩展

多个1 vs all分类器

首先尝试通过训练多个二元分类器（一类vs所有其他类），然后预测取\(\hat{y}=\arg\max_k(w_k^\top x+b_k)\)。

这么做的问题过多，比如每个分类器的权重可能都不在一个尺度上，并且每个分类器的正负输入量不一致。

多个1 vs 1分类器

一种改进是从一类vs所有其他类变成一类vs一类，训练\(\binom{k}{2}=\frac{K(K-1)}2\)个二元分类器，然后通过多数投票（majority voting）预测。

这种改进方法最大的问题就在最后的多数投票，可能会出现平票的问题，造成模糊性（ambiguity）

联合分类器

\[\begin{aligned} \min_{\mathbf{w},b} & \frac{1}{2}\sum_{y}\|\mathbf{w}_{y}\|^{2}+C\sum_{i=1}^{N}\sum_{y\neq y_{i}}\xi_{iy} \\ \mathrm{s.t.:~}\mathbf{w}_{y_{i}}^{\top}\mathbf{x}_{i}+b_{y_{i}} & \geq\mathbf{w}_{y}^{\top}\mathbf{x}_{i}+b_{y}+1-\xi_{iy}.\forall i,\forall y\neq y_{i} \\ & \xi_{iy}\geq0.\forall i,\forall y\neq y_{i} \end{aligned}\]

同时训练所有权重即可解决问题。

学习线性SVM的可扩展算法

对于超大数据集，需要一些具备可扩展性的算法来训练SVM。

标准的SVM训练方式需要计算\(N\times N\)的Gram矩阵，一次性计算和储存复杂度都过高。

线性算法Linear algorithm

切割平面法 Cutting-plane (2009)：

https://www.cs.cornell.edu/people/tj/publications/joachims_etal_09a.pdf

一次性处理所有约束条件过于复杂，可以先只包含很少的约束条件，求解SVM得到临时的\(\theta\)(\(w\)和\(b\))，然后对于最违反\(\theta\)的约束条件，纳入考虑范围，再次求解\(\theta\)，这样慢慢包含所有约束条件。

随机优化Stochastic optimization

随机梯度下降 Primal Estimated sub-GrAdient SOlver, Pegasos (2007)：

https://www.cs.huji.ac.il/~shais/papers/ShalevSiSr07.pdf

随机初始化\(w\)，通过在线学习的方法一步步纳入所有数据并更新权重。相比于上面的一步步纳入约束条件，这里一步步纳入数据。

分布式学习

Divide-and-conquer (2013)：

http://proceedings.mlr.press/v32/hsieha14.pdf

把输入分割为\(k\)份给不同的机器并行的训练SVM，然后通过合并所有模型的支持向量再训练一个最终SVM模型。

非线性SVM

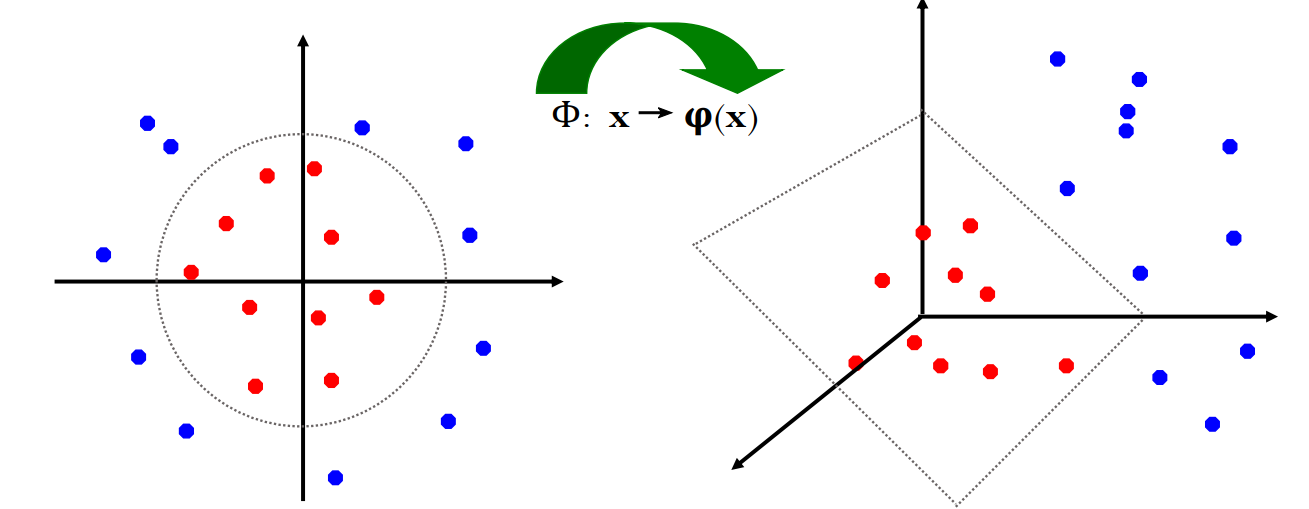
非线性SVM就是通过一个额外的函数\(\Phi\)将原始输入空间转换成一个更高维度的输入空间，并尽量使标签一样的数据集中，从而来找到一个超平面进行分割。

核方法Kernel Trick

正如前面提到的，线性SVM的对偶问题对于输入空间x只需要其Gram矩阵，也就是所有\(x_i^\top x_j\)，预测时也是通过计算所有\(x_i^\top x\)的值得出结果。

现在考虑非线性SVM，对于一个\(\Phi\)，尤其是极其复杂的高维输出的\(\Phi\)，计算\(\Phi(x_i)\)和\(\Phi(x_j)\)然后计算\(\Phi(x_i)^\top \Phi(x_j)\)是极其复杂及耗时的（甚至不知道\(\Phi\)的显式表达式，如无限维度的高斯核，下面会提到）。

但是如果存在核函数（kernel function）\(K\) s.t. \(K(x_i,x_j)=\Phi(x_i)^\top \Phi(x_j)\)，那么直接计算\(K\)即可省略以上（涉及高维的）步骤。

这里核函数的定义就是和某个输入空间的内积对应的函数。对于复杂的\(K\)，去核对对于所有\(x_i,x_j\)，\(K(x_i,x_j)=\Phi(x_i)^\top \Phi(x_j)\)是十分麻烦的。Mercer定理（或者其推广Moore-Aronszajn定理和再生核希尔伯特空间）指出

Every semi-positive definite symmetric function is a kernel

所有半正定对称函数（有对应的半正定对称Gram矩阵）都是核

通过这个定理可以快速判断不是核的函数（判断半正定性、对称性）。

三个例子：

1. 线性\(K(x_i,x_j)=x_i^\top x_j\)
2. 多项式\(K(x_i,x_j)=(1+x_i^\top x_j)^p\)
3. 高斯（径向基的一个实例）\(K(x_i,x_j)=\exp\left(-\frac{||x_i-x_j||^2}{2\sigma^2}\right)\)

深度神经网络也可以看作是一种可以学习的核，也叫神经正切核Neural Tangent Kernel。

径向基函数和径向基神经网络

径向基可以分为Radial（径向）和Basis（基）。

• Radial - 如果一个函数的值只依赖于输入点与某个“中心点”之间的距离，那么它就是“径向”的。
• Basis - 可以用作“积木”来构建更复杂的函数。

上述的高斯核只依赖输入\(x_i,x_j\)之间的距离（的平方），所以是Radial。考虑固定其中一个变量，\(f_{x_i}(x)=K(x_i,x)\)，所有的\(f_{x_i}(x)\)（\(x_i\)是支持向量）加起来就组成了原始问题对偶优化时（仅依赖每个\(K(x_i,x_j)=\Phi(x_i)^\top \Phi(x_j)\)）所需的Gram矩阵，也就是一组基函数。所以可以看出高斯核为什么是径向基。

考虑简化后的SVM决策函数（\(x_i\)是支持向量）：

\[f(\mathbf{x}) = \text{sign} \left( \sum_{i=1}^N (\alpha_i y_i) \cdot K(\mathbf{x}_i, \mathbf{x}) + b \right)\]

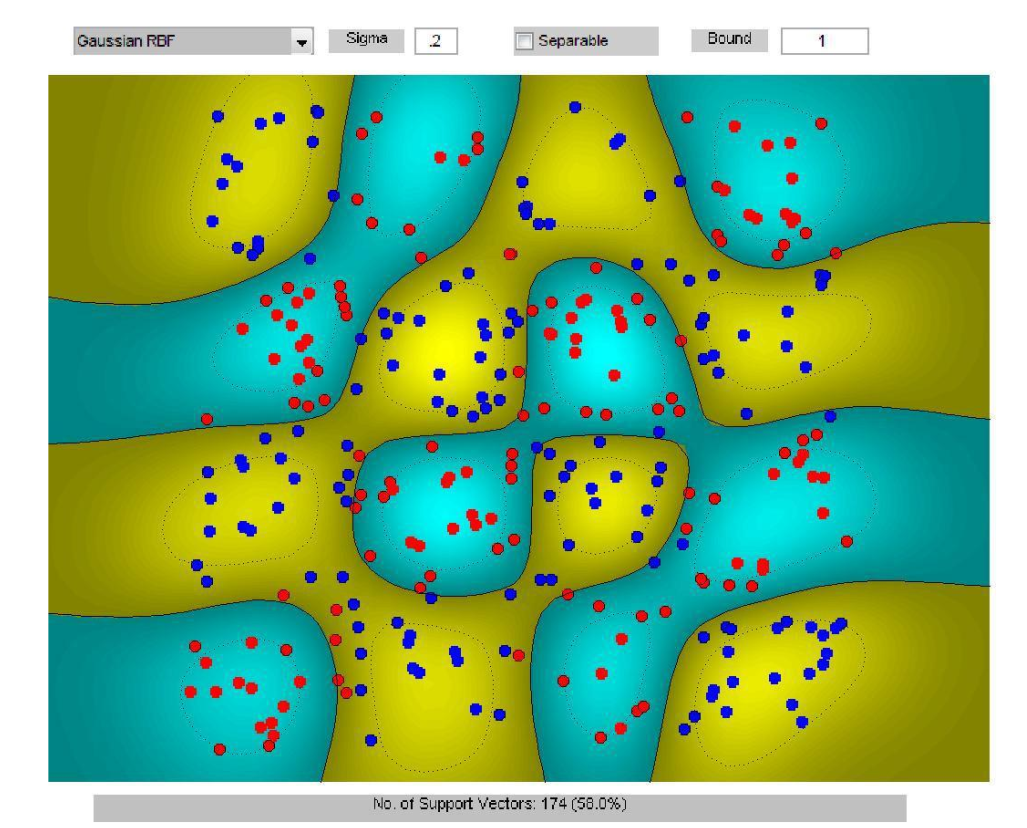
可以将这个决策函数想象成一个地形构建：

1. 在每一个支持向量 \(\mathbf{x}_i\) 的位置，我们放上一个“高斯鼓包”（或“凹陷”）。
2. 如果这个 \(\mathbf{x}_i\) 是红色 (\(y_i=1\))，我们就放一个正向的“鼓包”（把地形抬高，使其“偏向”红色）。
3. 如果这个 \(\mathbf{x}_i\) 是蓝色 (\(y_i=-1\))，我们就放一个负向的“凹陷”（把地形拉低，使其“偏向”蓝色）。
4. 每个“鼓包”或“凹陷”的高度由优化时决定的 \(\alpha_i\) 决定。
5. 最终的决策边界（对应上图黄色和蓝绿色的分界线），就是这个复杂地形上海拔为 0 的“海岸线”。

---

除了（最常用的）高斯核，还有这几个径向基函数：

1. Linear RBF: \(K(\mathbf{x}, \mathbf{y}) = ||\mathbf{x} - \mathbf{y}||\)
2. Multiquadric RBF: \(K(\mathbf{x}, \mathbf{y}) = \sqrt{c^2 + ||\mathbf{x} - \mathbf{y}||^2}\)
3. Inverse Multiquadric RBF: \(K(\mathbf{x}, \mathbf{y}) = \frac{1}{\sqrt{c^2 + ||\mathbf{x} - \mathbf{y}||^2}}\)

径向基的另外一个应用是径向基神经网络（RBF Network）：

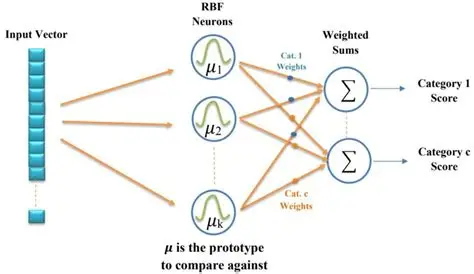
可以看出，径向基神经网络就是用径向基函数作为激活函数的浅层神经网络。

Platt 校准Platt Calibration

上面的SVM模型都只是预测输入是哪一类的判断，如果\(f(x)>0\)，即为\(+1\)类，反之亦然。

通过Platt 校准（也就是Sigmoid化）可以将输出转换成一个概率。

\[p(y=1|\mathbf{x})=\frac{1}{1+\exp(\alpha_1f(\mathbf{x};\boldsymbol{\theta})+\alpha_2)}\]

这里\(f\)是原始预测函数，\(\alpha_1,\alpha_2\)通过在训练数据上最大化条件似然来获得（SVM 训练完成之后）。

最大熵判别Maximum Entropy Discrimination (MED)

与其学习一组固定的模型参数\(\theta\)（即\(w,b\)），可以学习一个后验分布\(p(\theta)\)。

\[\begin{aligned} \min_{p(\boldsymbol{\theta}),\boldsymbol{\xi}} & \mathrm{KL}(p(\boldsymbol{\theta})\|p_0(\boldsymbol{\theta}))+C\sum_{i=1}^N\xi_i \\ \mathrm{s.t.:} & y_if(\mathbf{x};p(\boldsymbol{\theta}))\geq1-\xi_i,i\in[N] \\ & \xi_i\geq0,i\in[N], \end{aligned}\]

通过最小化先验分布和后验分布的KL散度加上损失\(C\sum_{i=1}^N\xi_i\)来找到最接近先验的分布，最后取期望值预测：

\[f(\mathbf{x};p(\boldsymbol{\theta}))=\mathbb{E}_{p(\boldsymbol{\theta})}[f(\mathbf{x};\boldsymbol{\theta})]\]

取高斯先验（先验为均值为0的正态高斯分布），对于线性模型MED简化成正常SVM。

学习非线性SVM的可扩展算法

\(N\times N\)的核矩阵\(G\)过于庞大，可以用一个\(N\times m\)的矩阵来近似。

低秩 Low-rank (2000)：

https://proceedings.neurips.cc/paper/2000/file/19de10adbaa1b2ee13f77f679fa1483a-Paper.pdf

从数据中随机采样\(m \ll N\)个点，只计算这些点和\(N\)个点之间的核值（假设这些为径向基函数），也就是计算维度为\(n\times m\)的矩阵，然后通过矩阵分解来近似完整的\(N\times N\)矩阵。

随机特征 Random-features (2007)：

https://people.eecs.berkeley.edu/~brecht/papers/07.rah.rec.nips.pdf

高斯核是无限维度（exp的泰勒展开有无限个项）的，但是我们可以通过随机采样的方式来近似这个无限维度核。

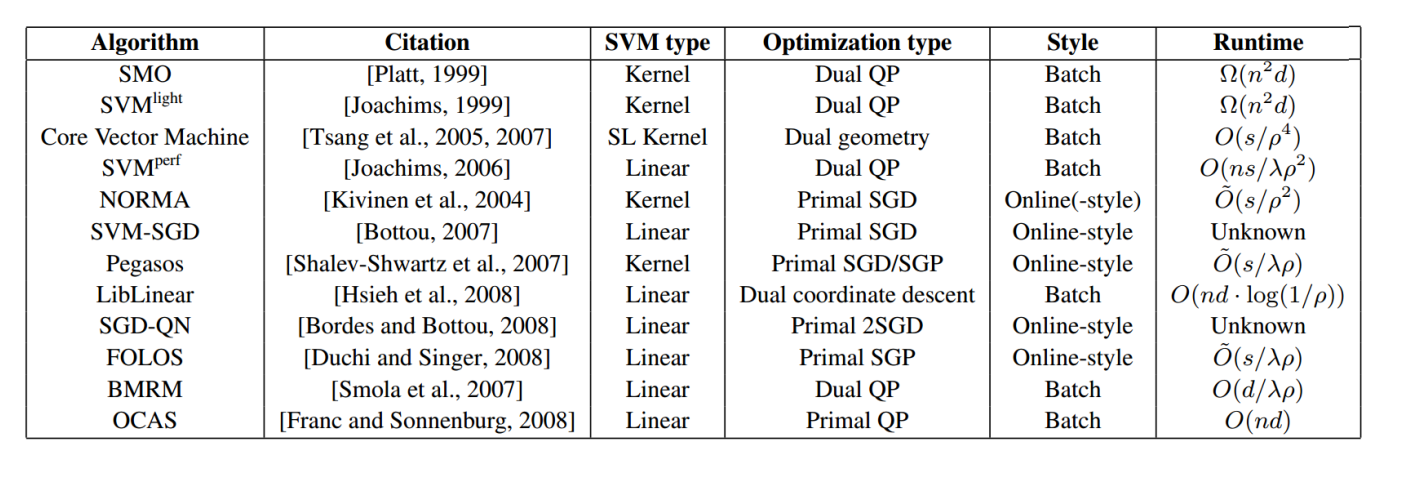
SVM算法列表

https://cseweb.ucsd.edu/~akmenon/ResearchExam.pdf

https://akmenon.github.io/papers/research-exam/research-exam-slides.pdf

截止2010：

KL