从经典算法到深度学习,AdaBoost、PCA、稀疏编码、与粒子滤波的重生与进化
随着基于注意力机制的大模型面临数据、算力、电力的限制,与对模型可解释性、可控性、推理能力的更高要求,深度学习领域出现了显著的“回溯现象”:人们纷纷将目光投向了前深度学习时代的经典算法思想。如,OpenAI 在 2025 年 11 月发布了通过稀疏电路来理解神经网络的文章:通过稀疏电路来理解神经网络 | OpenAI;还有像清华大学孙茂松老师团队在 2025 年 12 月发布的论文H-Neurons:大语言模型中幻觉相关神经元的存在、作用及其起源,基于 L1 稀疏线性回归器 Lasso 研究的幻觉相关神经元在神经网络的分布。
本文旨在深入探讨AdaBoost、主成分分析(PCA)、稀疏编码和粒子滤波这四大经典算法的基本思想在 2025 年大模型时代的重生与进化。通过对近三年论文的梳理与分析,得出结论:这些经典算法在本质上与现代大模型的对齐(Alignment)、高效微调(PEFT)、可解释性(Interpretability)及复杂推理(Reasoning)殊途同归。AdaBoost 的间隔理论与误差修正思想不仅解释了深度学习中的“良性过拟合”现象,更通过贝叶斯奖励模型集成(BRME)解决了 RLHF 中的奖励黑客问题;PCA 的低秩假设与流形理论直接催生了 LoRA-XS 等高效微调方法及 KV Cache 压缩技术,并揭示了模型本质上的线性特征;稀疏编码的基向量分解思想通过稀疏自编码器(SAE)破解了神经元超级叠加的可解释性难题,并推动了 MoE 架构与 Sparse-Linear Attention (SLA) 的演进;而粒子滤波的序列状态估计思想则为思维链(CoT)推理提供了概率论框架,并赋予视频生成模型掌握处理不确定性的物理世界模拟能力。这些经典思想正成为大模型从 System 1 向 System 2 跃迁的关键基石。
引言
在 2025 年的深度学习时代,或者说注意力机制驱动的多模态大模型时代,受限于算力与电力,人们从规模法则(scaling law)获取的收益越来越小,大模型正在从疯狂的通过优化算法来实现规模(scaling)化,到开始反思所有结构、组件、与细节。而现在很多关于大模型优化的最新论文都能看到十分多传统算法的影子,如课上讲的 AdaBoost,支持向量机(SVM),主成分分析(PCA),稀疏编码(Sparse Coding),粒子滤波(Particle Filtering)。在还没有实现连模型结构都能全部端到端训练的今天,能够通过前人发现与总结的先验知识来优化黑盒大模型至关重要。
本文将逐一分析以下四大算法在近三年技术语境下的映射关系:
- AdaBoost:从解释大模型为何能容忍极高噪声的“良性过拟合”理论,到利用 Boosting 思想集成奖励模型以提升 RLHF 的鲁棒性。
- PCA:将降维与特征提取思想极致化,演变为参数高效微调(如 LoRA-XS)的核心假设,以及解决超长上下文 KV Cache 瓶颈的关键手段。
- 稀疏编码:其过完备基向量分解思想重生为稀疏自编码器(SAE)成为目前解码大模型内部超级叠加的唯一有效工具;同时,其稀疏化思想重构了注意力机制(Sparse Attention),实现了计算效率的指数级提升。
- 粒子滤波:其序列状态估计与重采样思想被重新诠释为大模型的 System 2 思维链搜索策略,以及视频生成中处理时空不确定性的框架。
AdaBoost
间隔理论:AdaBoost 与 SVM 的相同本质
下面关于 AdaBoost 的早期研究参考了周志华老师在 2014 年的讲座:【报告】Boosting 25年(2014周志华)(up主推荐)_哔哩哔哩_bilibili
Kearns 和 Valliant 在 STOC’89 提出了可弱学习(存在准确率大于50%的模型)是否等价于可强学习(存在一个精度接近100%的模型)。随后的 1990 年 Schapire 从数学上证明了他们是等价的。
直到 1997 年,Schapire 和 Freund 才给出了可应用的算法 - AdaBoost。
基本来说,AdaBoost(Adaptive Boosting)通过给前面分类错误的样本添加一个指数级大的权重,来影响下一次模型迭代”分界线“,这样模型就会尽可能地尝试将这些之前被分类错误的样本正确的给分类出来。这样我们就可以看到:最影响模型边界的样本往往是那些很容易/一直被错误分类的样本,类似于 SVM 的支持向量 Support Vectors。
正如课上讲的,AdaBoost 最著名的一个应用就是基于 Haar 特征人脸检测的 Viola-Jones 检测器,它前几个阶段先只用 AdaBoost 的前几个弱分类器去检测人脸是否存在,通过了才会运行后面的弱分类器,这样大大的减少了计算量。
初始版本的 AdaBoost 人们无法解释为什么性能这么好,以及其实际优化目标是什么。Schapire 等人在 1998 年从间隔理论(Margin Theory)的角度给出了一个上界: \[ \epsilon_{\mathcal{D}}\le\mathbb{P}_{x\sim\mathcal{D}}(f(x)H(x)\le\theta)+\tilde{O}(\sqrt{\frac{d}{m\theta^2}+\ln\frac1\delta})\\ \le 2^T\prod_{t=1}^T\sqrt{\epsilon_t^{1-\theta}(1-\epsilon_t)^{1+\theta}}+\tilde{O}(\sqrt{\frac{d}{m\theta^2}+\ln\frac1\delta}) \] 其中 \(\theta\) 是间隔。可以看到样本数量 \(m\) 越大误差越小,模型复杂度越小误差越小,还有间隔越大误差越小。
上面的 \(\tilde{O}\) 展开来是 \(O\left(\frac{1}{\sqrt{m}}\left(\frac{\ln m\ln |\mathcal{H}|}{\theta^2}+\ln\frac1\delta\right)^{1/2}\right)\),可以看到是 \(O(\sqrt{\log m/m})\)。
基于最小化上述间隔的想法,Breiman 在 1999 年提出了一个更紧的上界: \[ \mathbb{P}_{\mathcal{D}}(yf(x)<0)\le R(\ln(2m)+\ln\frac1R+1)+\frac1m\ln\frac{|\mathcal{H}|}{\delta} \] 其中 \(\theta>4\sqrt{\frac{2}{|\mathcal{H}|}}\) 和 \(R=\frac{32\ln 2|\mathcal{H}|}{m\theta ^2}\le 2m\) 可以看到是 \(O(\log m/m)\)。
基于这个理论,Breiman 同时设计了一个基于 AdaBoost 的变种 arc-gv,通过直接最大化最小间隔来优化算法(类似于SVM)。问题是实验结果看下来虽然最小间隔(minimum margin)确实是比 AdaBoost 更好了,但测试误差也变大了许多。
于是,为了找到更好的解释来让测试误差也最小化,与其优化最小间隔,随后的研究开始考虑优化间隔分布(margin distribution)。王立威等人在 2011 年给出了一个具体的基于间隔分布的更紧的上界,也是 \(O(\log m/m)\),但问题是引入了 KL 散度的概念。也就是,由于考虑了额外的信息,还是无法确定间隔分布是否比最小间隔更本质。
周志华老师等人在 2013 年提出的第 \(k\) 个间隔界(\(k\)-th margin bound)给出了一个真正的间隔分布的界: \[ \mathbb{P}_{\mathcal{D}}(yf(x)<0)\le\frac2m+\\ \inf_{\theta\in(0,1]}\left[\mathbb{P}_S(yf(x)<\theta)+\frac{7\mu+3\sqrt{3\mu}}{3m}+\sqrt{\frac{3\mu}{m}\mathbb{P}_S(yf(x)<\theta)}\right] \] 这里 \(\mu=\frac{8}{\theta^2}\ln m\ln(2|\mathcal{H}|)+\ln\frac{2|\mathcal{H}|}{\delta}\)。可以看到是 \(O(\log m/m)\)。可以证明这个界比 Breiman 和 Schapire 的界都一致更紧,并且用到的信息完全一样。准确来说,通过一些变换,上面的界可以变换为考虑平均间隔(average margin)和间隔方差(margin variance),那就是,同时考虑这两个属性比考虑最小间隔更本质。Shivaswamy 和 Jebara 在 2011 年也已经给出了同时最大化平均间隔和最小化间隔方差的算法,结果也是十分完美。
于是,从 AdaBoost 这方面的研究,可以对支持向量机(SVM)进行改进。
传统的 SVM 模型是通过最大化最小间隔来进行优化收敛的,基于上面的研究,我们可以看到用平均间隔和间隔方差来优化 SVM 理论上模型测试误差会比传统的要好。
周志华老师等人在 2014 年也发表了这篇论文肯定了相关的优化。
深度学习时代大模型的双重下降与良性过拟合
随着深度学习时代的到来,尤其是当模型参数量远超样本数量(即过参数化机制)成为常态时,经典理论与规模法则(scaling law)基本冲突。传统经典理论无法解释大模型规模化(scaling)带来的的许多现象。
Reconciling modern machine-learning practice and the classical bias–variance trade-off | PNAS
Belkin 等人在 2019 年提出了“双重下降”这个概念,并提出传统机器学习的U型曲线仅适用于欠参数化(under-parametrized)的模型。
更具体的,在传统机器学习和统计学中,测试误差往往对模型复杂度呈现U型曲线:欠拟合(模型复杂度过低、容量过小;记不住数据的基本特征)、拟合的刚好、过拟合(模型复杂度过高、容量太大;数据的噪声影响过大)。
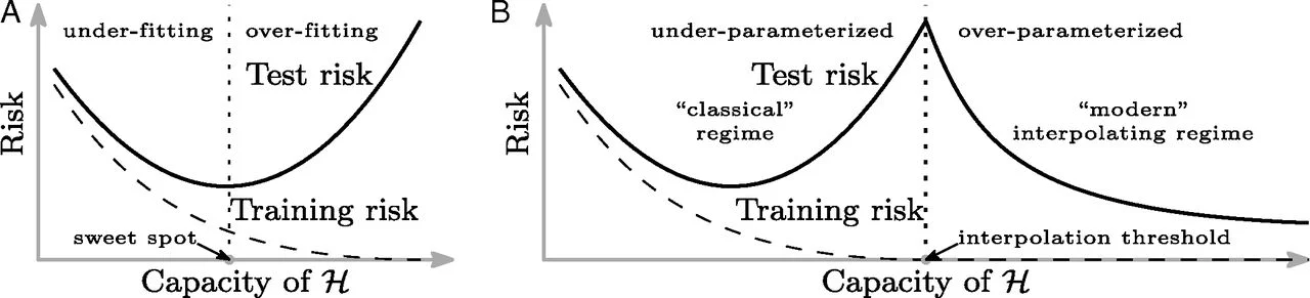
但如上图右边所示,在现代深度学习大模型中,观测到了测试误差在过拟合后会再次下降甚至优于传统的最优点。随着参数(模型容量、复杂度)的增加也分为三个阶段:U型曲线阶段、测试误差最高的临界点(噪音影响最大)、在这之后随着参数量的增加,测试误差重新下降。
Surprises in High-Dimensional Ridgeless Least Squares Interpolation
Hastie 等人同年证明了不仅是深度模型。对于线性回归模型,参数数量 \(p\) 与样本数量 \(n\) 的比值 \(\gamma = p/n \approx 1\) 时,方差会趋向无穷大(因为求逆矩阵变得极不稳定)。也就是,\(p=n\) 是临界点。
Deep Double Descent: Where Bigger Models and More Data Hurt
OpenAI 在同年将 Belkin 等人的理论推广到了现代深层神经网络(CNN,Transformer),并发现不仅在“模型容量(模型复杂度、大小)”这个概念有双重下降这个现象,在网络深度、宽度、训练轮数(Epoch)各个方面都出现了双重下降。
对于这个反常现象,出现了几种解释。
现代插值区间
Belkin 等人在 2019 年的论文还提出了现代插值区间(Modern Interpolation Regime)这个概念:当模型大到足以记住所有训练数据时,它倾向于通过选择“范数最小”(Minimum Norm)的解来平滑函数,从而获得良好的泛化能力。
顿悟现象
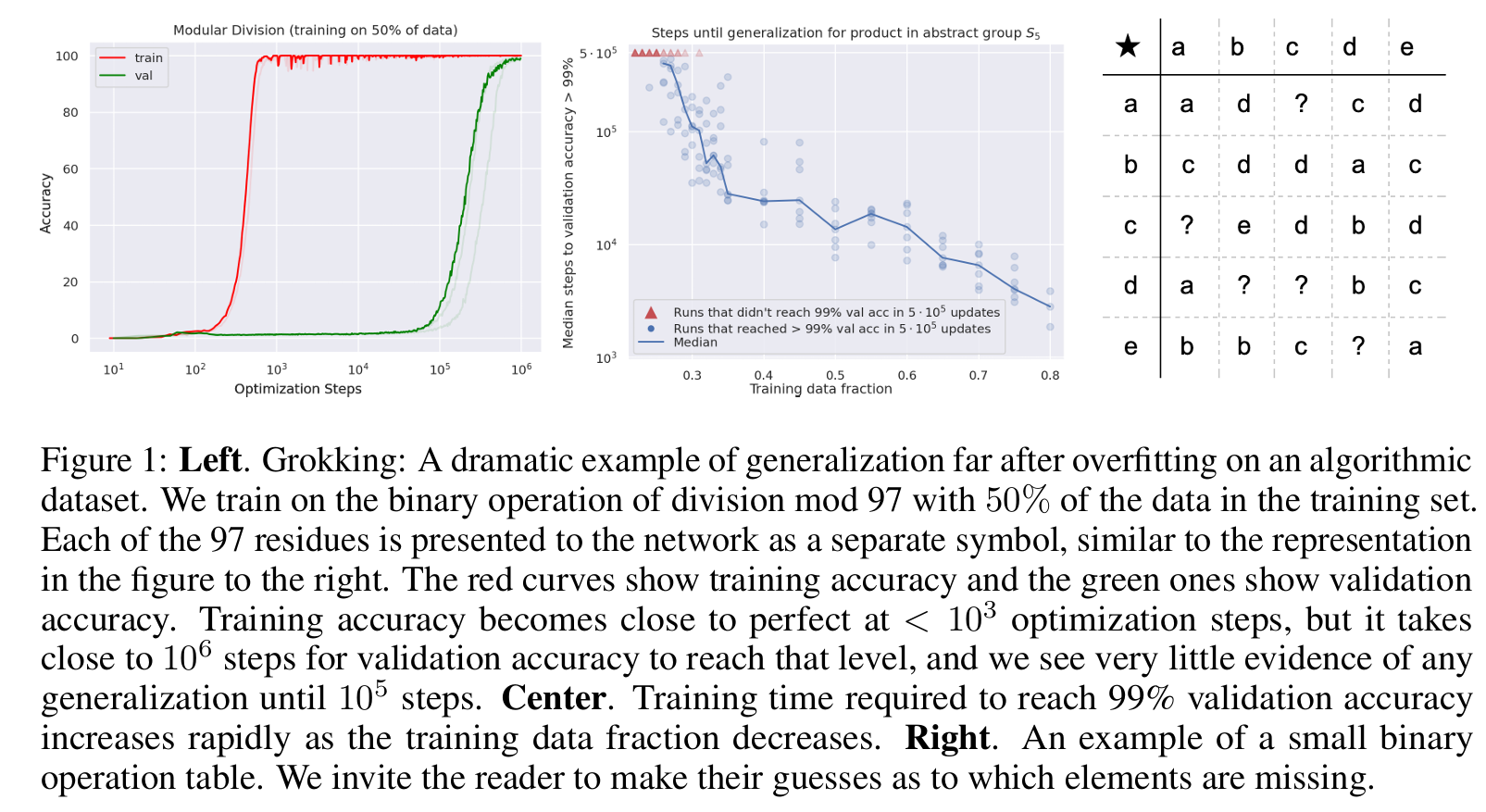
Grokking: Generalization Beyond Overfitting on Small Algorithmic Datasets
Power 等人在 2022 年提出了关于训练轮数(Epoch)双重下降的解释:随机梯度下降 SGD 在“记住数据”之后,还在暗中优化模型的内部结构以寻找更平滑的解。
可以看到,这种解释类似于人对人脑学习的理解,先死记硬背,然后尝试从中找出规律,然后记住规律,这样遗忘的时候会优先遗忘死记硬背的实际输入。
良性过拟合
Benign Overfitting in Linear Regression
Bartlett 等人在 2020 年提出了良性过拟合(Benign Overfitting)来解释双重下降:即便模型完美拟合了噪声数据,如果多余的参数能让解的范数分布得足够“均匀”,那么噪声的影响就会被稀释。
更具体的,通过引入有效秩(Effective Ranks)\[r_k(\Sigma) = \frac{\sum_{i>k} \lambda_i}{\lambda_{k+1}}\] 用于用于衡量尾部的“迹”相对于尾部最大特征值的比例,以及 \[R_k(\Sigma) = \frac{\left( \sum_{i>k} \lambda_i \right)^2}{\sum_{i>k} \lambda_i^2}\] 用于衡量尾部能量分布的均匀程度。对于线性回归模型 \(y = x^\top \theta^* + \epsilon\),其中 \(x\) 是特征向量,\(\theta^*\) 是真实的最佳参数,\(\epsilon\) 是均值为 0、方差为 \(\sigma^2\) 的噪声;协方差矩阵 \(\Sigma = \mathbb{E}[xx^\top]\)。设其特征值为 \(\lambda_1 \ge \lambda_2 \ge \dots \ge 0\);定义最小范数插值解(Minimum Norm Interpolator) \[\hat{\theta} = \arg\min_{\theta: X\theta=\mathbf{y}} \|\theta\|_2\],其存在闭式解 \[\hat{\theta} = X^\top (XX^\top)^{-1} \mathbf{y}\];以及有效维度 \[k^* = \min \{ k \ge 0 : r_k(\Sigma) \ge b n \}\] 用来区分主要与次要的特征方向。可以得出结论,对于最小范数解 \(\hat{\theta}\),其超额风险 \(R(\hat{\theta}) = \mathbb{E}[(x^\top \hat{\theta} - x^\top \theta^*)^2]\) 满足: \[ R(\hat{\theta}) \le C \left( \underbrace{\|\theta^*\|^2 \sqrt{\frac{\text{tr}(\Sigma)}{n}}}_{\text{Bias}} + \underbrace{\sigma^2 \left( \frac{k^*}{n} + \frac{n}{R_{k^*}(\Sigma)} \right)}_{\text{Variance}} \right) \] 其中,偏差(Bias)通常很小,而方差(Variance)可以分为两个部分:如果主要的特征维度远小于样本量 \(n\),那么 \(\frac{k^*}{n}\) 也小;如果 \(R_{k^*}(\Sigma) \gg n\),这说明尾部有大量非零特征值,且分布比较均匀。这就表示噪声被稀释到这无数个微小的维度上,每个维度分到的“错误”微乎其微,从而使得总预测误差很小。
于是,结合这两个部分,可以推导出:只要 \(\frac{k^*}{n}\to0\),并且 \(R_{k^*}(\Sigma) \gg n\) 也就是 \(\frac{n}{R_{k^*}}\to0\),那么超额风险也趋于 0,也就是所谓的良性过拟合。
从间隔理论解释良性过拟合
从之前关于 AdaBoost 的研究可以看到,即便训练误差已达到零,模型仍能通过最大化平均间隔和最小化间隔方差来提升泛化性能。
最大化平均间隔
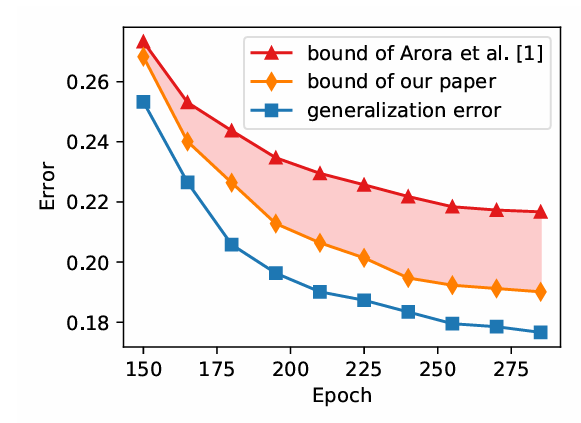
Improving Generalization of Deep Neural Networks by Leveraging Margin Distribution
周志华老师等人在上面 2018 年的论文指出随着模型训练的进行,传统的 SGD 其实本质上还是在最大化最小间隔(使用交叉熵 CE 损失函数)。基于间隔理论的想法,他们提出了凸间隔分布损失函数(mdNet Loss),可以不断增加归一化后的平均间隔。
更具体的,定义间隔为 \[\gamma_{h}(x,y) = f_{w,y}(x) - \max_{j\ne y}f_{w,j}(x)\],其中 \(f_{w,y}(x)\) 是网络对正确标签 \(y\) 的输出,\(f_{w,j}(x)\) 是对其他类别 \(j\) 的输出。定义凸间隔分布损失函数(Convex Margin Distribution Loss Function,mdNet Loss)为: \[ l_{r,\theta,\eta}(h(x),y) = \begin{cases} \frac{(r - \theta - \gamma_{h})^2}{(r - \theta)^2} & \text{if } \gamma_{h} \le r - \theta \\ 0 & \text{if } r - \theta < \gamma_{h} \le r + \theta \\ \frac{\eta(r + \theta - \gamma_{h})^2}{(r + \theta)^2} & \text{if } \gamma_{h} > r + \theta \end{cases} \] 那么可以证明泛化误差上界比传统 SGD 配合交叉熵更好: \[ L_{0}(f_{w}) \le \hat{L}_{r,\theta}(f_{w}) + \mathcal{O}\left(\sqrt{\frac{(\frac{1+\lambda}{1-\lambda})^{2}(\sum_{i=1}^{d}\frac{d \rho \alpha^{2}c^{2}}{\mu_{i}^{2}\mu_{i\rightarrow}^{2}}) + \ln\frac{6m}{\delta}}{m}}\right) \] 其不仅与最小间隔有关,还和间隔比率(Margin Ratio)\[\lambda = \frac{\theta}{r}\] 有关。也就是,泛化误差与 \(\frac{1+\lambda}{1-\lambda}\) 成正比。因此,算法的目标是获得更小的 \(\lambda\),即更大的平均间隔 \(r\) 和 更小的方差 \(\theta\)。
并且,论文还推导了网络输出对参数扰动的敏感度,证明了允许的噪声水平 \(\sigma^2\) 与间隔分布的关系: \[ \max_{x \in X} |f_{w+u}(x) - f_{w}(x)|_{2}^{2} \le \mathcal{O}\left(\sum_{i=1}^{d}\frac{d\alpha^{2}c^{2}\sigma^{2}(r+\theta)^{2}}{\mu_{i}^{2}\mu_{i\rightarrow}^{2}}\right) \] 这进一步导出了允许的噪声方差 \(\sigma^2\) 与间隔分布的关系: \[ \sigma^2 \propto \left(\frac{1-\lambda}{1+\lambda}\right)^2 = \left(\frac{r-\theta}{r+\theta}\right)^2 \] 也就是,如果SGD能成功优化出更紧凑的间隔分布(更小的 \(\lambda\)),网络就能容忍更大的参数扰动而不改变分类结果,从而实现更好的泛化。
尽管这篇论文给出的理论结果十分完美,因交叉熵配合 SGD 的鲁棒性与高效计算,业界并未采用。
最小化间隔方差
On the Benefits of Over-parameterization for Out-of-Distribution Generalization
此外,类似于前面的顿悟现象,张潼教授等人在 2024 年发现,对于 ReLU 随机特征模型(Random Feature Model)在双重下降(Double Descent)曲线的第二下降阶段(即参数量极度丰富时),模型能够找到一种更加平滑的解。这种平滑性在几何上表现为特征空间中样本分布的正交性(Orthogonality)增强。也就是,当特征维度极高时,样本向量之间趋于正交,这种几何结构天然地降低了投影到决策方向上的(间隔)方差。
更具体的,考虑过参数化的 ReLU 随机特征模型 \[ f_{W}(\theta,x)=\frac{1}{\sqrt{m}}\phi(x^{T}W)\theta \] 以及其最小范数估计量 \[ \hat{\theta}(W)=\Phi_{W}^{T}(\Phi_{W}\Phi_{W}^{T})^{-1}y \] 其中 \(\Phi_{W} \in \mathbb{R}^{n \times m}\) 是训练数据的特征矩阵。
假设 SGD 找到了最小范数解,并且数据满足良性过拟合的几何条件。那么,ReLU 网络的核矩阵 \(K\) 可以被一个线性化的矩阵 \(\tilde{K}\) 近似: \[ \tilde{K} = \underbrace{\frac{tr\{\Sigma\}}{p}\left(\frac{1}{2\pi}+\frac{3r_{0}(\Sigma^{2})}{4\pi tr\{\Sigma\}^{2}}\right)\mathbf{1}\mathbf{1}^{T}}_{\text{Bias}} + \underbrace{\frac{1}{4p}XX^{T}}_{\text{Linear}} + \underbrace{\frac{tr\{\Sigma\}}{p}\left(\frac{1}{4}-\frac{1}{2\pi}\right)I_{n}}_{\text{Identity}} \] 其中,偏差项是常数;\(XX^T\) 的线性项代表样本间的内积,也就是样本间的相关性;最后的正交项可以看到,当特征维度极高且满足良性过拟合条件时,这一项保证了核矩阵的特征值主要由对角线元素主导。也就是,在几何上这意味着样本在特征空间中几乎是相互正交的。
尽管这个发现无法推广泛化到所有深度模型,但还是可以从理论上完美解释部分良性过拟合的原因。
通过 AdaBoost 的误差修正思想增加 RLHF 的鲁棒性
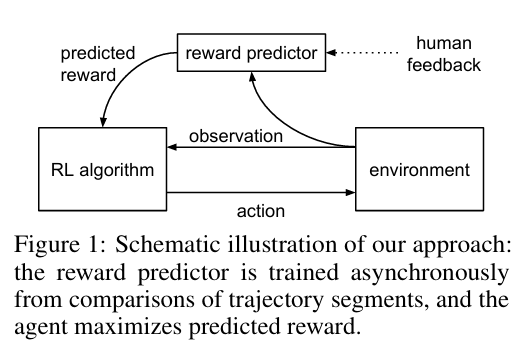
ChatGPT 最著名的一项核心技术就是人类反馈强化学习(Reinforcement Learning from Human Feedback,RLHF):Deep reinforcement learning from human preferences。
RLHF 通常由三个阶段构成:首先通过有监督微调(Supervised Fine-Tuning,SFT)在高质量指令数据集上初始化模型,使之具备基础的指令遵循能力;随后进入奖励建模(Reward Modeling)阶段,利用人类对模型生成结果的标度或排序反馈(Ranking),训练一个标量奖励模型来拟合人类的判别逻辑;最后,在强化学习(RL)阶段,利用如 PPO 等策略优化算法,以奖励模型的实时打分作为环境反馈,对语言模型进行迭代优化,从而实现模型输出在有用性、真实性及安全性上的帕累托改进。
然而,单一的奖励模型(Reward Model,RM)往往存在盲点,导致策略模型(Policy Model,即LLM)学会利用这些盲点获取高分,却输出人类不希望看到的内容,即奖励黑客(Reward Hacking)现象:Concrete Problems in AI Safety。
为了解决这个问题,清华大学的严谕梓等人引入了 AdaBoost 的误差修正思想:Reward-Robust RLHF in LLMs。
贝叶斯奖励模型集成
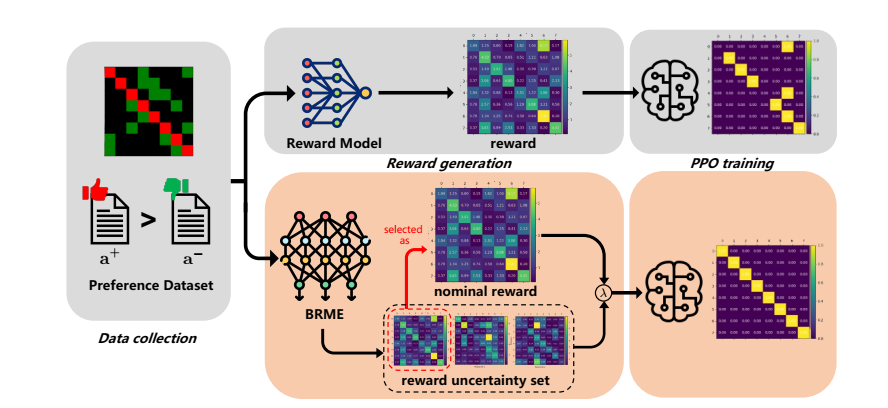
为了解决单一 RM 无法有效捕捉分布外(Out-Of-Domain,OOD)的偏好不确定性,以及由此导致的奖励黑客问题,上述论文提出了贝叶斯奖励模型集成(Bayesian Reward Model Ensembles,BRME)。
训练
传统的 RM 通常输出一个标量作为奖励值,但这无法反映模型对当前评分的置信度。为此,BRME 引入了贝叶斯多头(Multi-head)结构,每个头 \(i\) 输出的是一个高斯分布 \(\mathcal{N}(\mu_i, \sigma_i)\) 而非单一标量。
更具体的,对于输入 \(x\) 和回复 \(a\),第 \(i\) 个奖励头的输出由均值 \(\mu_i\) 和标准差 \(\sigma_i\) 决定,最终奖励值通过重参数化(Reparameterization)采样获得: \[ r_i = \mu_i + \alpha \cdot \sigma_i, \quad \alpha \sim \mathcal{N}(0, 1) \] 这种设计通过 \(\sigma_i\) 让奖励值 \(r_i\) 不仅基于评分,还基于其不确定性(置信度)。
其中,为了让标准差 \(\sigma\) 能够真正反映模型的置信度,BRME 先使用传统的 Bradley-Terry 模型损失函数训练一个标准的单头 RM,作为初始的“标称”信号(最大似然估计,MLE);然后,引入均方误差(MSE)损失函数对多头 BRME 进行训练。论文从理论上证明了,对于 MSE 损失函数 \(l_i\),其对标准差的梯度 \(\mathbb{E}[\nabla_{\sigma} l_i] \ge 0\)。也就是,随着优化的进行,为了最小化损失,模型倾向于降低 \(\sigma\),从而使得 \(\sigma\) 的大小能够作为衡量模型置信度的有效指标。
基于此,BRME 定义了标称奖励(Nominal Reward) \(\hat{r}\):在推理阶段,选择所有头中标准差 \(\sigma_i\) 最小(即置信度最高)的那个头的均值作为标称奖励。
优化
基于 AdaBoost,或者说 Boosting 模型的集成(Ensemble)思想,BRME 的目标函数不仅追求奖励最大化,还考虑最坏情况: \[ J_{\lambda}(\theta) := \lambda J_{perform}(\theta) + (1-\lambda) J_{robust}(\theta) \] 其中 \(J_{perform}\) 基于标称奖励 \(\hat{r}\),代表模型对“最好情况”的估计;\(J_{robust}\) 基于不确定性集合 \(\mathcal{R}^{uncertain}\) 中的最小奖励(Min Reward),即 \(\min_{r \in \mathcal{R}^{uncertain}} r(x,a)\)。
通过调整超参数 \(\lambda\),模型平衡利用标称信号和规避最差情况。这种策略有效地防止了策略模型(Policy Model,即LLM)过度优化那些带有高不确定性的错误高分区域,规避了奖励黑客。
此外,严谕梓等人还得出了低估奖励比高估更可取的结论。也就是,如果 RM 对错误行为给出了过高的分数,RL 算法(如 PPO)会迅速利用这一漏洞,导致模型性能崩溃。另外一边,他们的随机案例分析(Stochastic Case Analysis)证明了,当奖励被低估甚至退化为常数时,梯度的方差减小,策略更新趋于保守,模型会缓慢回退到 SFT 阶段的初始状态,而不会像遇到高估奖励那样发生灾难性遗忘或模式坍塌。
小结
虽然间隔理论最早是通过 SVM 研究的,但周志华老师等人的基于 AdaBoost 的研究将间隔理论完美完善了。可以看到,间隔理论即使是在深度学习大模型时代的今天仍有一席之地。
而 AdaBoost,或者说 Boosting 族的模型最核心的思想,误差修正,也被广泛应用在许多算法与模型,如上面介绍的 BRME。
主成分分析 - PCA
主成分分析(PCA)的基本思想是在降低数据维度的同时,最大程度地保留原始数据的信息(即方差)。其核心假设是:高维数据通常分布在一个低维流形上(流形假设),绝大多数方差(信息)由少数几个正交的主成分解释。
在算力和显卡内存受限的今天,能够通过修改低维参数来近似高维大模型的修改至关重要,现在绝大多数主流的参数高效微调(PEFT)方法都受到了上述低维适应(Low-Rank Adaptation)假设的启发,或者说,基于内在维度(Intrinsic Dimensionality)假设。
内在维度假设
Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning
Aghajanyan 等人在 2020 年提出了内在维度(Intrinsic Dimensionality)假设:预训练模型虽然参数巨大,但解决特定下游任务所需的参数更新其实存在于一个极低维度的子空间内。这与 PCA 的思想不谋而合。
更具体的,大型预训练模型具有极强的表征能力,微调时并不需要改变所有权重。通过将全量参数 \(\theta\) 投影到一个随机的低维子空间 \(d\)(其中 \(d \ll D\)),在这个小空间内进行优化,依然能达到全量微调 90% 以上的效果。
低秩自适应 - LoRA
LoRA: Low-Rank Adaptation of Large Language Models
目前最流行的微调技术为低秩自适应(Low-Rank Adaptation, LoRA),其假设预训练模型权重为 \(W_0\in\mathbb{R}^{d\times d}\),更新后的权重为 \(W = W_0 + BA\),其中 \(B \in \mathbb{R}^{d \times r}, A \in \mathbb{R}^{r \times d}\),且秩 \(r \ll d\)。
也就是,模型适应新任务所需的权重变化矩阵是低秩的,这对应了上述的内在维度假设。
LoRA-XS:用奇异值分解初始化低秩矩阵
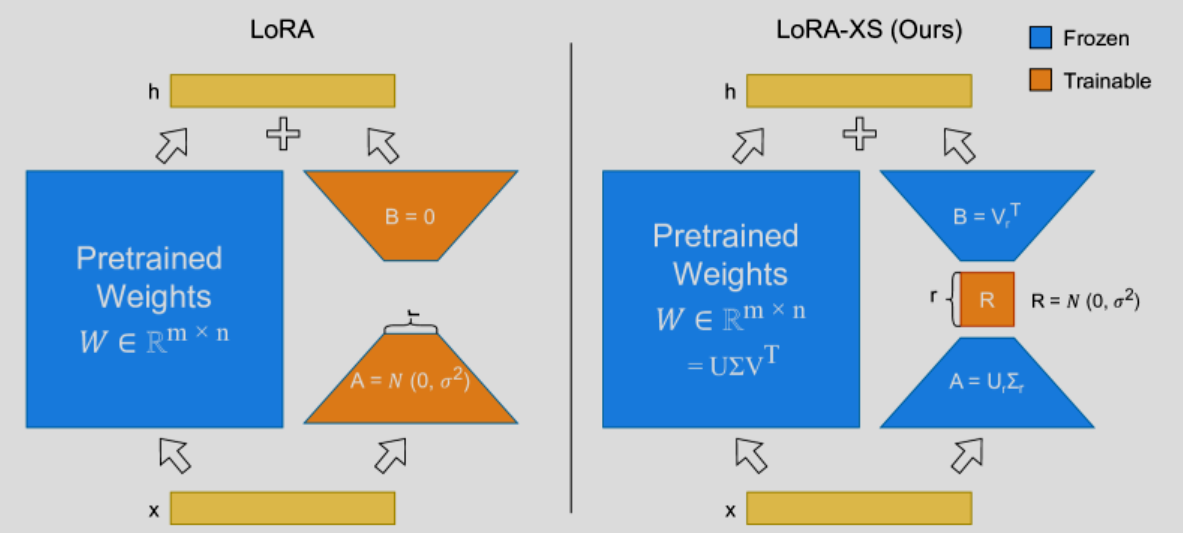
LoRA-XS: Low-Rank Adaptation with Extremely Small Number of Parameters
传统 LoRA 通过高斯随机初始化矩阵 \(B A\)。上面的 2025 年研究表明,低秩矩阵 \(B A\) 的初始化参数可以通过预训练权重 \(W\) 的奇异值分解(SVD)来初始化。
更具体的,因为预训练权重矩阵 \(W\) 的主要信息可以通过其 SVD 的前 \(r\) 个分量来近似,所以,与其像标准 LoRA 那样重新学习低秩投影矩阵(\(A\) 和 \(B\)),LoRA-XS 认为这些投影方向(基底)可以直接复用预训练权重的特征方向,只需学习这些方向之间的重组关系。
从上图可以看到,LoRA-XS 不仅冻结了预训练权重 \(W\),还冻结了 \(B \in \mathbb{R}^{d \times r}, A \in \mathbb{R}^{r \times d}\),仅训练一个 \(\mathbb{R}^{r\times r}\) 的矩阵 \(R\),大大减少了需要调整的参数量。并且实验表明,这种方法在多个下游任务上不仅收敛速度更快,而且最终性能优于随机初始化的 LoRA - 因为它精准地捕捉了权重空间的主成分方向。
更严谨的,从数学上看,假设预训练模型的某个权重矩阵为 \(W_0 \in \mathbb{R}^{m \times n}\),对其进行奇异值分解:\[W_0 = U \Sigma V^\top\]。然后,取前 \(r\) 个最大的奇异值及其对应的奇异向量(\(r\) 为设定的秩,例如 8, 16 等),得到近似 \[W_0 \approx U_r \Sigma_r V_r^\top\],其中 \(U_r \in \mathbb{R}^{m \times r}\),\(\Sigma_r \in \mathbb{R}^{r \times r}\),\(V_r^\top \in \mathbb{R}^{r \times n}\)。然后如上图所示,冻结 \(A:=U_r \Sigma_r\),\(B:=V_r^\top\)。
也就是,LoRA-XS 将 LoRA 的 \[ W = W_0 + \Delta W = W_0 + B A \] 变为 \[ W = W_0 + \Delta W = W_0 + s \cdot B R A \] 其中 \(s\) 是缩放因子(Scaling factor),通常设为 \(1\) 或类似于 LoRA 的 \(\alpha/r\)。
这就将原本两个需要训练的 \(B \in \mathbb{R}^{d \times r}, A \in \mathbb{R}^{r \times d}\) 变为仅训练 \(R\in \mathbb{R}^{r\times r}\)。需要训练的参数量从 \[ N_{LoRA} = r \times n + r \times m = r(n + m)\] 变为仅 \[ N_{LoRA-XS} = r \times r = r^2 \] 与大模型的维度完全无关,仅取决于秩 \(r\)。
这种在潜在空间(Latent Space)训练的思想不仅对应了 PCA 使用主成分向量降低数据维度,也完美对应了自编码器(AutoEncoder,AE)将复杂的高维空间数据压缩到低维进行表示的思想。
KV Cache压缩
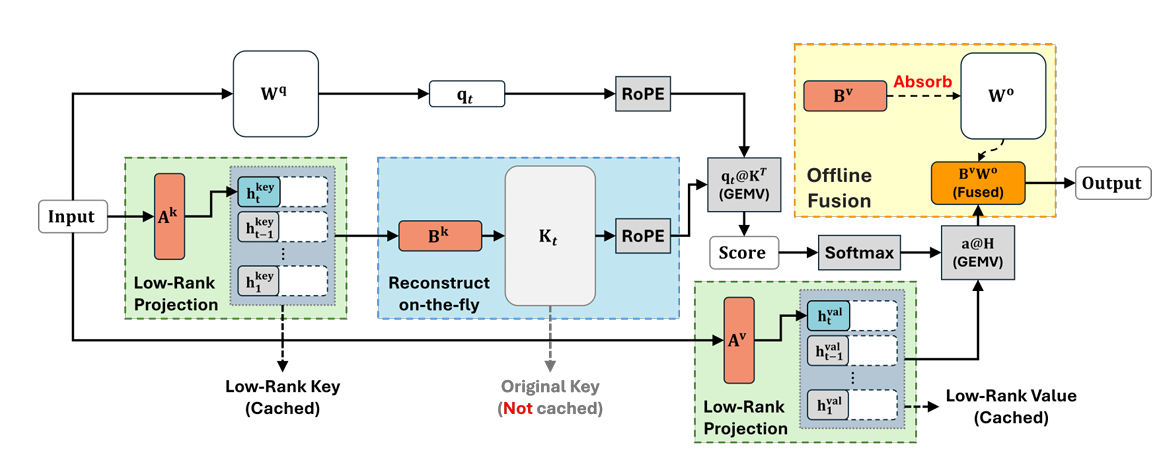
Palu: Compressing KV-Cache with Low-Rank Projection
随着 Transformer 注意力机制的大模型越来越关于超长上下文给用户带来的正向体验,上下文长度逐渐扩展到了上百万 Token,而推理时的 Key-Value (KV) Cache 占用的显存成为巨大瓶颈。传统的量化(Quantization)只能减少数据精度,而无法减少维度。更具体的,传统 KV Cache 中的张量形状为 (Layer, Head, Seq_Len, Dim),随着 Seq_Len 增长,显存线性爆炸。
2024 年的上文对 KV 特征矩阵进行 PCA 分析,发现其有效秩(Effective Rank)远低于模型维度 \(D\)。也就是,这意味着大量的维度是冗余的。
于是,他们设计了以下算法:
- 先在少量校准数据上收集 Key 和 Value 的激活值。
- 计算这些激活值的协方差矩阵,并进行特征值分解,得到投影矩阵 \(P \in \mathbb{R}^{D \times d'}\),其中 \(d' \ll D\)。
- 在推理时,存储压缩后的 \(K' = K P\) 和 \(V' = V P\)。
从结果上来看,通过这种基于 PCA 的低秩投影,可以在保留 90% 以上模型性能的前提下,将 KV Cache 的大小压缩 60% 至 75%。这直接验证了 PCA 在处理海量神经激活数据时的高效性。
大模型的可解释性
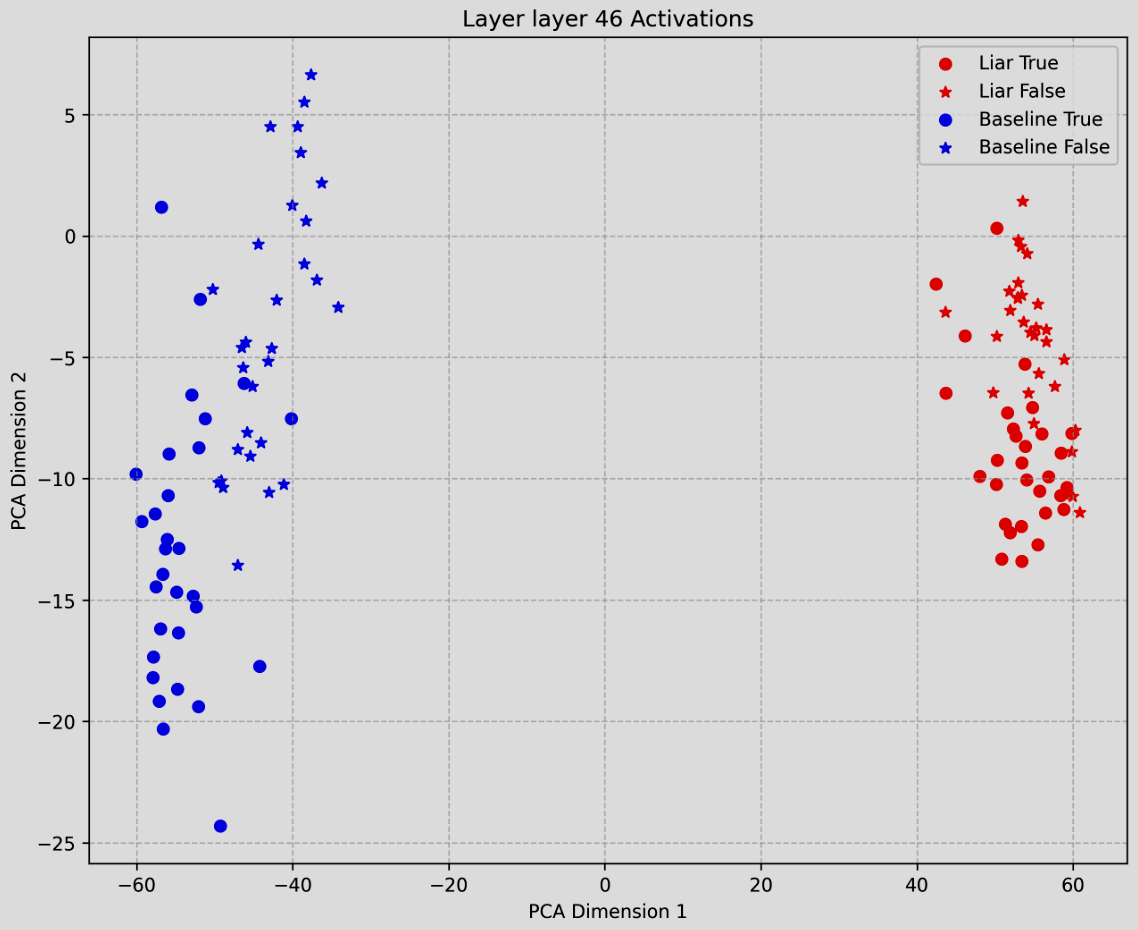
PCA 的思想还深刻的用在了大模型的可解释性与控制领域。
When Thinking LLMs Lie: Unveiling the Strategic Deception in Representations of Reasoning Models
这篇 2025 年的论文发现,在具有思维链(CoT)能力的推理模型中,用 PCA 将高维隐层状态投影到 2D 平面后,代表“诚实”和“欺骗”的样本点在 PCA 空间中是线性可分的。
基于这种线性可分性,论文提出了 Linear Artificial Tomography (LAT) 方法,通过提取欺骗向量(Deception Vectors)来检测模型是否在说谎。通过利用这种简单的线性探测(Linear Probing),论文在检测战略欺骗方面达到了约 89% 的准确率,进一步印证了诚实与欺骗信号在表示空间中的线性本质。
线性 PCA 是如何处理深度学习模型非线性空间的
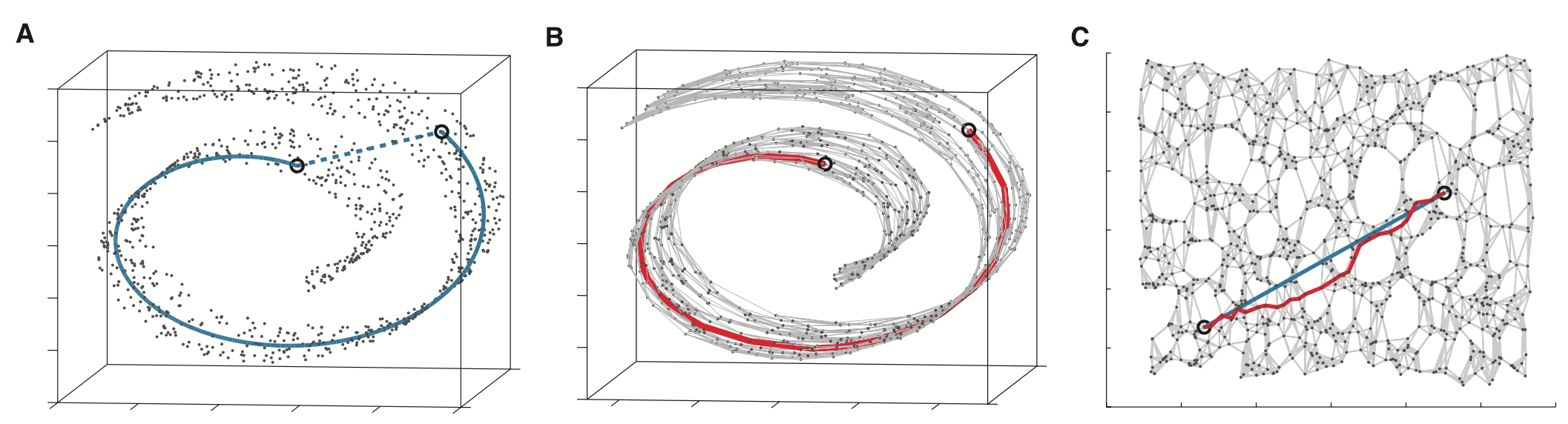
在上一小节,我们提到了用 PCA 将高维隐层状态投影到 2D 平面的可能性。但,我们这里假设了所有深度学习模型的高维隐层状态都是可以通过线性工具 PCA 来降维投影的。本小节将探讨线性 PCA 为什么在非线性神经网络也能成功应用,其如何处理如上图瑞士卷般的数据空间的。
上面这 2022 年的篇文章提出了 超级叠加(Superposition)的概念:模型利用高维空间的几何特性,将多于维度的特征压缩进低维空间。
也就是,模型会把特征编码为线性方向。这对应了词嵌入空间中我们常看到的的 \(\vec{V}(\text{北京}) - \vec{V}(\text{中国}) \approx \vec{V}(\text{东京}) - \vec{V}(\text{日本})\)。
Towards Monosemanticity: Decomposing Language Models With Dictionary Learning Anthropic
在此之上,Anthropic 在 2023 年通过应用稀疏自编码器(SAE),证明了可以将大语言模型(LLM)中原本混乱、多义的神经元,分解为单义(Monosemantic)的特征方向。下一节将会深入探讨稀疏自编码器。
The Linear Representation Hypothesis and the Geometry of Large Language Models
上面论文在同年也探讨了为什么梯度下降倾向于学习线性表示。可以证明,在数据由潜在特征驱动、使用交叉熵损失以及梯度下降趋向范数最小化的条件下,梯度下降最优的表示结构必然是线性的。
也就是,对于瑞士卷形状的数据空间,大模型会通过非线性函数(如 ReLU,Sigmoid)展平(Flattening),将其变为一个平整的线性空间,从而实现最优拟合。
基于以上研究,可以看出即使神经网络作为万能函数逼近器(universal function approximator),其核心表达方式仍为线性。也就是,我们仍可以将机器学习时代到早期深度学习时代的各种工具应用到基于神经网络的深度学习大模型上。
小结
PCA 通过低维向量表示高维空间的核心思想在深度学习大模型时代也并不过时,反而因为算力与显存受限,人们越来越需要低维近似了,正如何凯明等人在 2025 年发表的 JiT 论文,通过让模型拟合(基于流形假设的)低维数据空间,而非高维噪音空间,来返璞归真,大大降低硬件压力。
稀疏编码 - Sparse Coding
稀疏编码的核心理念与 PCA 十分相近,他们都是试图通过一组某种意义上的基向量(Basis Vectors)的线性组合来重构原始数据。但他们的基向量与最终形式有着本质的区别。
简单来说,PCA 追求的是正交与信息压缩,而稀疏编码追求的是特征的稀疏性与可解释性。
更具体的,无论是 PCA 还是稀疏编码,它们在数学表达上都可以看作: \[ X \approx \sum_{i=1}^{k} a_i \phi_i \] 其中 \(X\) 是原始输入,\(\phi_i\) 是基向量(或主成分),\(a_i\) 是对应的系数(权重)。
可以看到,他们都试图通过基变换(Change of Basis)将原始空间转换为一个更有特点的线性空间。
PCA 的目标是找到数据中方差最大的方向,通过投影来实现降维。也就是,各个基向量之间互不相关,但每个样本都需要由大部分主成分组成。
与之相反的,稀疏编码希望每个样本仅由极少数的基向量组成,这导致了基向量无法互不相关。这也可以看出,稀疏编码的基向量通常是过完备(Overcomplete)的,意味着基向量的数量 \(k\) 甚至可以大于原始维度 \(n\)。
综上,可以看到 PCA 试图找到整个数据空间更为本质的表达方式(降维),而稀疏编码试图找到所有样本更为简洁的表达方式(可以是通过降维或升维)。
超级叠加(Superposition)
正如在主成分分析的一小节提到的,大模型存在一个现象:一个神经元往往同时响应完全不相关的概念。
Towards Monosemanticity: Decomposing Language Models With Dictionary Learning Anthropic
Anthropic 将这种现象解释为 超级叠加(Superposition):模型为了在有限的维度内存储超过维度数量的特征,利用高维空间中“几乎正交”的方向来压缩存储特征。
为了解开这种纠缠,模型必须将密集的激活向量投影回稀疏的高维基向量。这正是基于陶哲轩等人提出的压缩感知与稀疏编码的经典定义:\(x \approx \sum a_i \phi_i\),其中系数 \(a\) 是稀疏的。
稀疏自编码器
稀疏自编码器(Sparse Autoencoder,SAE)就解决了上面的问题。
Sparse Autoencoders Find Highly Interpretable Features in Language Models
Scaling and evaluating sparse autoencoders
稀疏自编码器最早由吴恩达 (Andrew Ng) 及其斯坦福大学团队在 2000 年代后期通过一系列课程和论文(如 CS294A 课程讲义)将其系统化并推广到深度学习领域,但直到 2023-2024 年,Anthropic 和 OpenAI 的研究者才将其重新发扬光大,用于解决大语言模型(LLM)的可解释性问题。
稀疏自编码器通过以下方式实现稀疏编码(Sparse Coding):
编码器(Encoder):将大模型的激活 \(x\)(维度 \(d\))映射到极高维的隐层 \(f\)(维度 \(M \gg d\))。 \[ f = \text{ReLU}(W_{enc} x + b_{enc}) \]
稀疏约束: 在损失函数中加入 L1 正则项,也是稀疏编码的标志性操作。 \[ L = ||x - \hat{x}||^2 + \lambda ||f||_1 \]
解码器(Decoder): 重构原始信号。解码器的权重 \(W_{dec}\) 的列向量即为提取出的“特征字典”。
通过以上的 SAE 训练,原本混杂的神经元被分解为数百万个具有高度单一语义的特征(Features)。
如,Anthropic 发现,Claude 3 Sonnet 的 SAE 提取出了专门响应“旧金山金门大桥”、“代码安全漏洞”、“特定编程语言语法”的特征。并且这些特征是单义的(Monosemantic),即它们只对单一概念激活。
Sparse Autoencoders Learn Monosemantic Features in Vision-Language Models
此外,在多模态模型的 2025 年,这篇论文也展示了 SAE 还可以提取出代表特定视觉概念(如“某种鸟类的喙”)的神经元,即便这些概念在原始模型中是与其他概念叠加存储的。
混合专家模型 - MoE
稀疏自编码器尝试将模型的某些层映射到高维激活空间,通过解耦来稀疏化神经元,寻找稀疏的特征表示。
而混合专家模型(Mixture of Experts,MoE)通过路由在权重空间实现了计算稀疏性:对于一个 Token,整个网络仅有少部分神经元参与计算。
更具体的,MoE 将稠密的前馈神经网络(Feedforward Network,FFN)分解为多个独立的专家(Expert)网络,并引入门控网络(Gating Network / Router)决定每个输入 Token 应该激活哪些(专家)网络。
对于输入 \(x\),MoE 的输出 \(y\) 可以表示为: \[ y = \sum_{i=1}^{N} G(x)_i E_i(x) \] 其中 \(N\) 是专家总数,\(E_i(x)\) 是第 \(i\) 个专家的输出,\(G(x)_i\) 是门控网络输出的权重系数。可以看到,这个公式完美对应了稀疏编码的公式 \[x \approx \sum a_i \phi_i\]
DeepSeek-V2: A Strong, Economical, and Efficient Mixture-of-Experts Language Model
DeepSeek 当初的火爆离不开相比当时美国大模型的及其廉价的成本,而这个成功离不开其使用的 DeepSeekMoE 架构。由此可见,MoE 带来的成本下降十分显著。
并且,MoE 不仅从计算成本上给出进步,还让神经网络权重稀疏化带来的宽度扩展极大的增加了模型的容量与表达能力。
稀疏注意力:从量化压缩到稀疏线性分解
如果说 SAE 是在特征维度(Feature Dimension)上寻找稀疏的基向量,那么稀疏注意力(Sparse Attention)则是在 时间 / 序列 维度(Sequence Dimension)上寻找稀疏的关联关系。
对于现在所有基于 Transformer 与其注意力机制的大模型来说,\(O(N^2)\) 大小的注意力权重矩阵十分巨大。
注意到,每个 token 并非和所有其他 token 都相关。所以,有办法将此矩阵稀疏化,用低维,或特殊形式表示尤为重要。
这一小节将基于清华大学陈键飞与朱军老师的 TSAIL 团队在 2024-2025 年对注意力的研究,从量化压缩到动态稀疏再到稀疏化配合线性分解,解释他们团队目前优化注意力权重矩阵的流程。
SageAttention:量化压缩
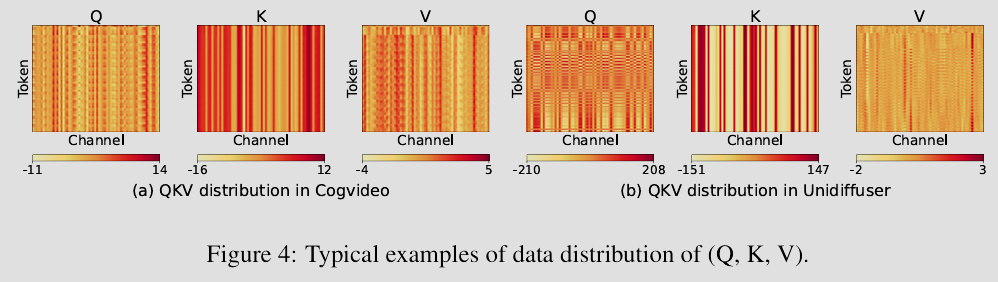
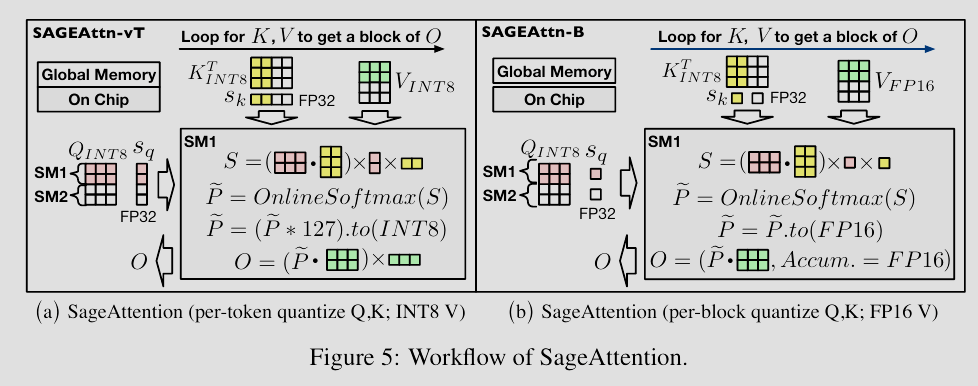
SageAttention: Accurate 8-Bit Attention for Plug-and-play Inference Acceleration
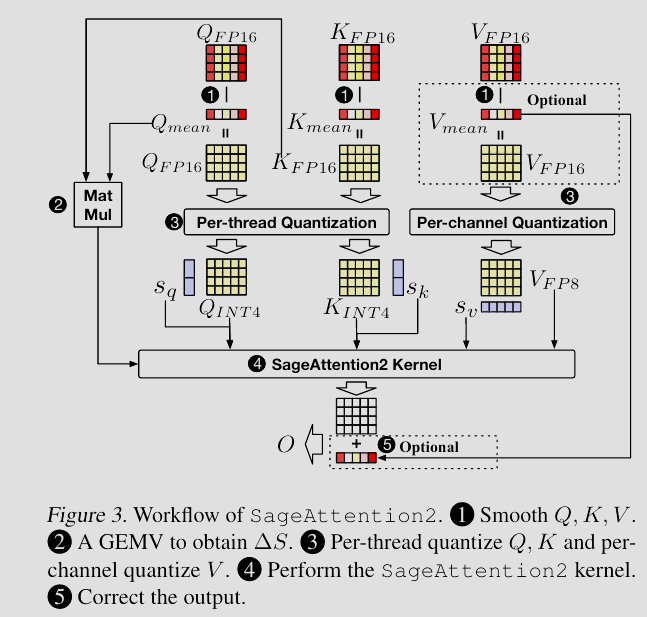
SageAttention2: Efficient Attention with Thorough Outlier Smoothing and Per-thread INT4 Quantization
首先,团队注意到了在注意力机制中,Query 和 Key 矩阵中存在的异常值会导致直接量化(如 INT8)的精度损失极大。于是,SageAttention 提出了一种类似于基变换的平滑技术,将这些尖锐的异常值抹平,使得数据分布更均匀,从而能够被低比特编码无损表示。
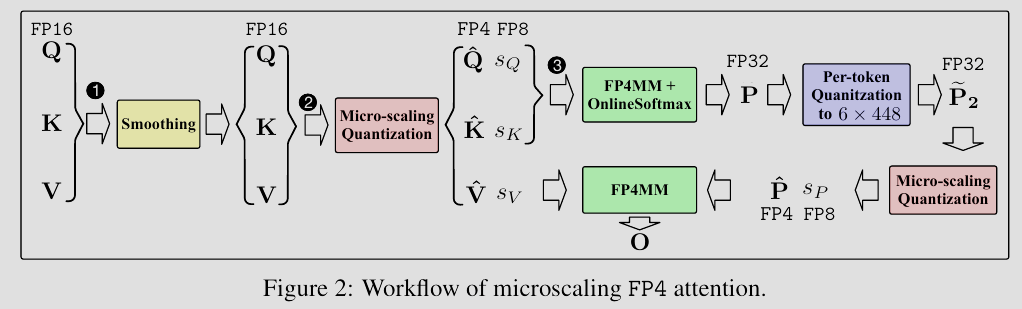
SageAttention3: Microscaling FP4 Attention for Inference and An Exploration of 8-Bit Training
到 2025 年,SageAttention 进一步演变成 SageAttention3。通过上图的微缩放(Microscaling)技术,模型甚至可以在 FP4(4-bit浮点) 的极低精度下进行注意力推理而不损失精度。这表明了了注意力矩阵的信息熵其实本质上极低,我们甚至可以用极短的编码长度(4-bit)来还原原始的高维交互信息。
SpargeAttention:动态稀疏筛选
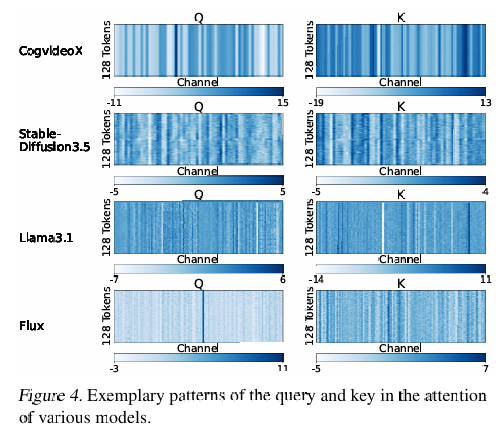
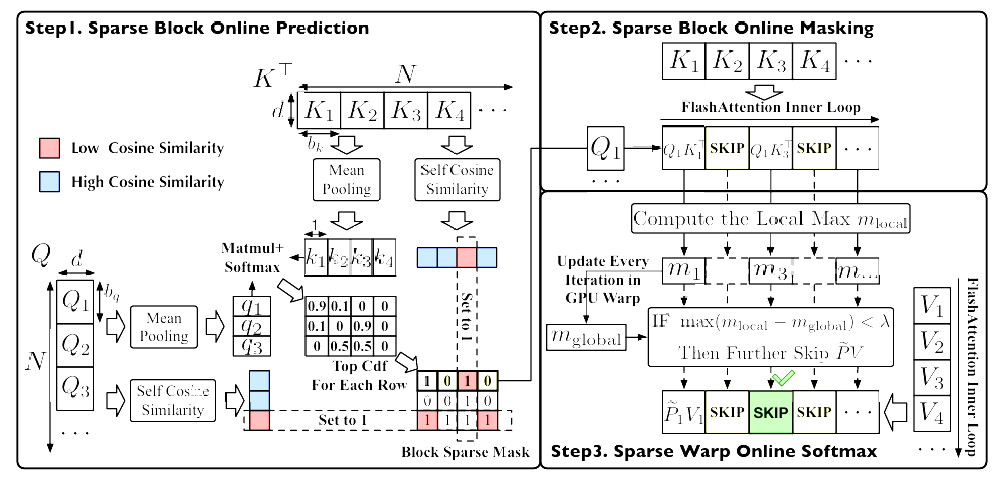
SpargeAttention: Accurate and Training-free Sparse Attention Accelerating Any Model Inference
SageAttention 尝试将每个计算单元变小,而 SpargeAttention 则是从稀疏化的角度尝试将计算单元变少。也就是,让整个注意力权重矩阵变得更加稀疏化。这对应了稀疏编码中 \(a_i\) 系数的稀疏性。
更具体的,论文发现注意力图本质上是稀疏的,而许多现有的稀疏方法,如滑动窗口都是基于规则的,静态的。为了解决这个问题,SpargeAttention 提出了一种动态的两阶段过滤机制:
- 粗粒度筛选(Coarse-grained): 利用块级别的代表性 Token(的平均值)计算相似度。如果一个块内的 Token 高度自相似(Self-similar),则可以被压缩;如果该块与 Query 不相关,则直接在计算图中被置零。
- 细粒度筛选(Fine-grained): 在 Warp 级别利用在线 Softmax 的统计特性,进一步剔除那些即使计算了也对最终结果贡献微乎其微的元素。
Sparse-Linear Attention(SLA):分解高频与低频信息
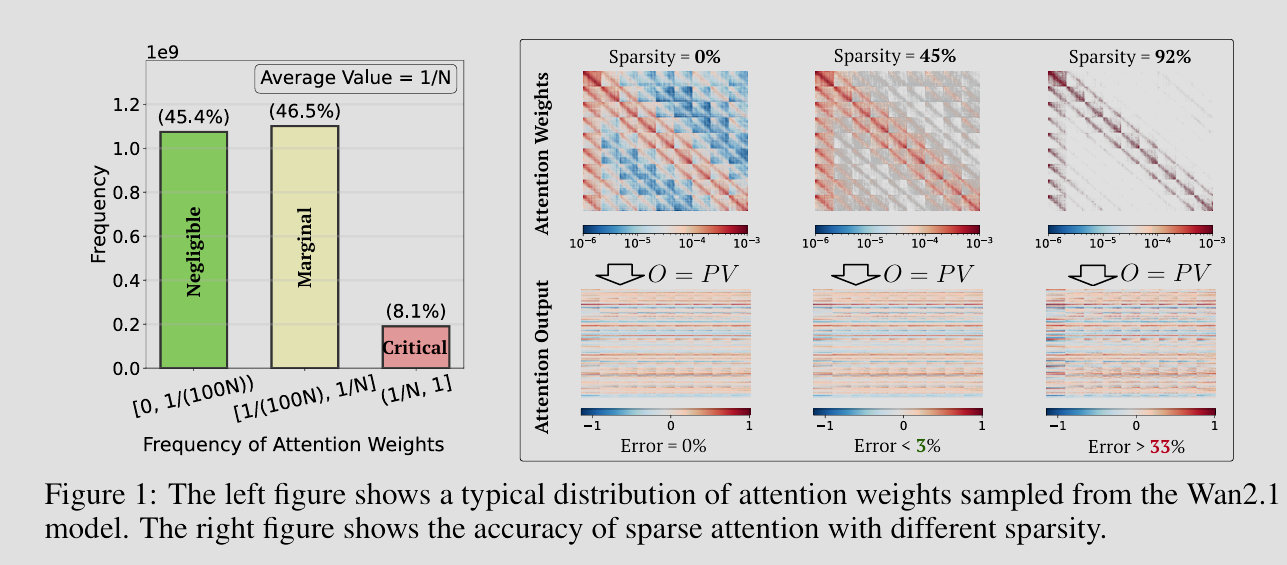
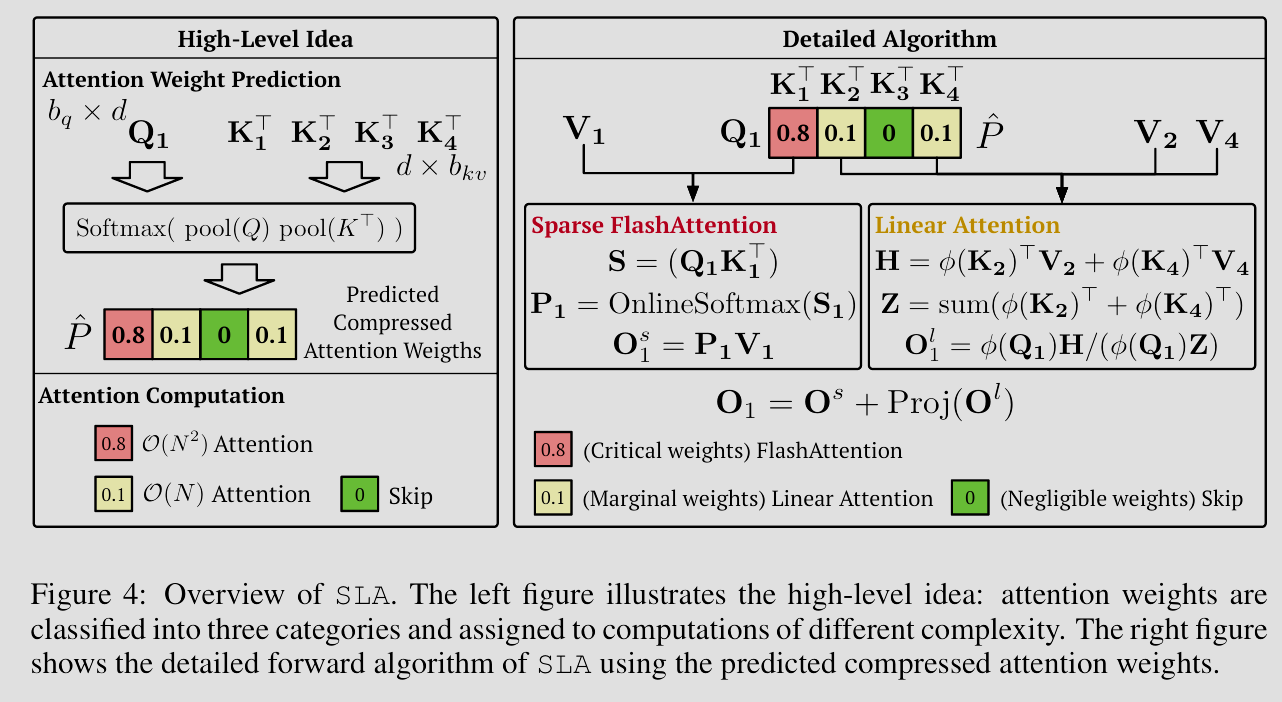
SLA: Beyond Sparsity in Diffusion Transformers via Fine-Tunable Sparse-Linear Attention
前面的稀疏注意力虽然减少了计算单元,但其实也造成了全局信息的丢失。稀疏编码虽然抓住了高频特征,但低频的背景信息因稀疏化不可避免地被忽略了。
为此,引入类似于鲁棒主成分分析和稀疏加低秩分解的思想,SLA 将注意力分解为: \[ \text{Attention}(Q, K, V) \approx \underbrace{\text{Sparse}(Q, K, V)}_{\text{高频细节}} + \underbrace{\text{Linear}(Q, K, V)}_{\text{全局低频}} \] 其中,稀疏(Sparse)分支使用类似 SpargeAttention 的方法,只计算那些相关性极强(Top-\(k\))的注意力分数,负责生成纹理与细节;而线性(Linear)分支用来近似被稀疏分支忽略的背景信息,负责生成构图与整体色调。
换句话说,论文证明了大模型的注意力机制可以被解耦成少量的强连接(对应了上文的稀疏高频细节)和大量的弱连接(对应了上文的低秩、线性全局低频)。这种分解不仅在 Diffusion Transformer(DiT)上取得了超越全量注意力的效果,更是从本质上分解了神经网络内部信息流动的两种不同的模式。
thu-ml/TurboDiffusion: TurboDiffusion: 100–200× Acceleration for Video Diffusion Models
他们团队在 2025 年近期发布的 TurboDiffusion 扩散模型的上百倍速度提升也离不开其内核 SageAttention 与 SLA 的贡献,展现了他们的实用性。
小结
超级叠加在某种意义上来说与人们追求的(对人类而言的)可解释性相冲突,如上文 OpenAI 也在尝试通过稀疏电路来提升模型的可解释性。
但脑科学研究表明,人脑本质上也是稀疏化的超级叠加(人脑的 860 亿个神经元中,只有极少数约 1% 到 4% 在特定时刻活跃),与主流 MoE 架构类似。这或许表明了对于人类期望的 AGI,MoE 的稀疏结构是必不可少的。但对于超级智能 ASI,其终极形态究竟是复杂的超级叠加,还是极具可解释性的稀疏化与解耦,人们尚且不知。
粒子滤波 - Particle Filter
粒子滤波,或者更广泛地说说序列蒙特卡洛(Sequential Monte Carlo, SMC),其核心源自冯诺依曼等人提出的蒙特卡洛近似思想,几乎是目前解决高维解空间、逼近非解析数学精确解的通用方法。
如,为了模拟现实世界的复杂光照,计算机图形学的光线路径追踪算法(Ray Tracing)完全利用蒙特卡洛积分模拟漫反射,来逼近渲染方程的解。又如,蒙特卡洛树搜索(MCTS)几乎是 AI 博弈游戏必须的方法。
但蒙特卡洛树搜索不仅可以用在双方博弈的极小极大状态树中,其处理状态不确定性和搜索规划的能力也十分重要。而现代深度学习大模型的思维链(Chain of Thought,CoT)本质上也可以看作是在所有符合逻辑的思维链中搜索最优。也就是,其将推理视为一个动态系统,利用序列采样的思想,在庞大的潜在逻辑路径中,搜索并构建出最优的思维轨迹。
粒子滤波
处理动态系统状态估计最早的算法当属卡尔曼滤波。但其线性和高斯假设让其很难实际应用到现实中的很多非线性动力学或多峰分布。而粒子滤波的非线性与非高斯假设让其能够完成绝大多数任务。
粒子滤波基于隐马尔可夫模型(HMM),假设状态空间存在隐藏状态 \(s_t \sim P(s_t | s_{t-1})\) 和观测值 \(o_t \sim P(o_t | s_t)\)。
然后,由于后验分布 \(P(s_{0:t} | o_{1:t})\) 通常极其复杂并且无解析解,粒子滤波使用序列蒙特卡洛,通过 \(N\) 个加权粒子 \(\{(s_t^{(i)}, w_t^{(i)})\}_{i=1}^N\) 来近似后验分布:
首先,根据先验采样新状态 \(s_t^{(i)} \sim q(s_t | s_{t-1}^{(i)}, o_t)\)。
然后,根据观测值 \(o_t\) 计算粒子的权重。如果粒子预测的状态成功解释了观测数据,增加其权重: \[ w_t^{(i)} \propto w_{t-1}^{(i)} \frac{P(o_t|s_t^{(i)}) P(s_t^{(i)}|s_{t-1}^{(i)})}{q(s_t^{(i)} | s_{t-1}^{(i)}, o_t)} \]
最后,为了防止权重退化,复制高权重粒子,剔除低权重粒子进行重采样。
思维链 - CoT
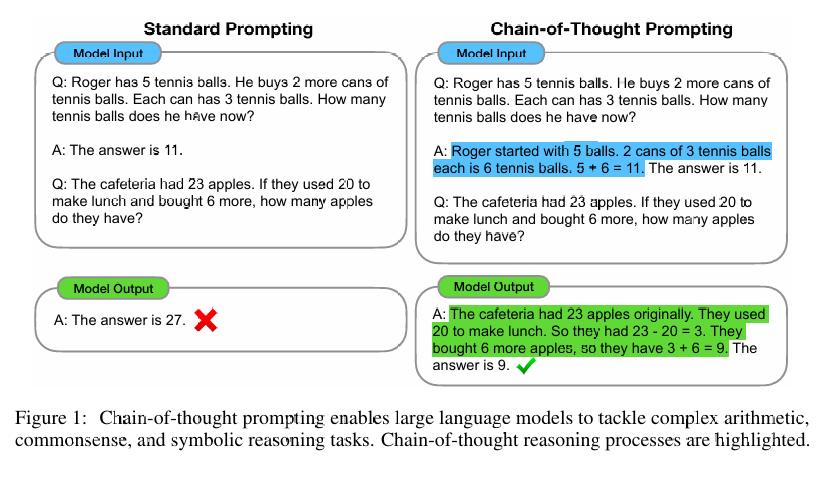
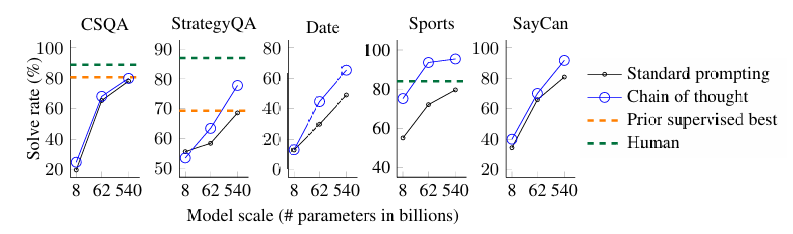
Chain-of-Thought Prompting Elicits Reasoning in Large Language Models
正如 Daniel Kahneman 的《Thinking, Fast and Slow》提出的人类认知的双系统理论所说,人类有两个思维系统:
- 直觉系统(快思考系统, System 1) - 无意识、快速、自动化的反应(如看到人脸识别情绪,听到声音转向)。依赖于亿万年进化形成的生物本能和长期训练的直觉。
- 逻辑系统(慢思考系统, System 2) - 有意识、缓慢、耗能的分析与计算。需要注意力高度集中。此外,还负责监控System 1的冲动。
传统的大语言模型直接学习一个从输入 \(x\) 到输出 \(y\) 的映射关系,可以看到这本质上就是 System 1 的极致体现:基于概率直觉快速生成文本,反应迅速但容易出错(幻觉),且缺乏逻辑监控。
由谷歌团队在 2022 年提出的思维链(Chain of Thought,CoT)技术就试图让模型拥有人的 System 2 思维能力。
他们注意到,对于需要多步逻辑的问题,直接映射 \(x \to y\) 会因计算深度不足而失败。为此,CoT 引入潜变量(Latent Variables),将直接预测 \(P(y|x)\) 转化为联合概率建模 \(P(y, z|x)\): \[ P(y|x) = \sum_{z} P(y|z, x)P(z|x) \] 其中 \(z\) 是思维过程,然后寻找最优路径: \[ \hat{y} = \arg\max_{y} P(y|\hat{z}, x) \] 其中 \(\hat{z} \approx \arg\max_{z} P(z|x)\)。
这强制模型生成中间推理步骤 \(z = (z_1, z_2, \dots, z_n)\),然后再生成答案 \(y\),用时间换空间(模型深度),变相提升了其深度思维的能力。
可以看到,思维链的核心思想与粒子滤波并无不同:
- 粒子滤波的时间 \(t\) 对应了思维链推理的深度或步骤。
- 粒子滤波的状态 \(s_t\) 对应了思维链推理的具体思维片段。
- 粒子滤波的粒子对应了思维链推理具体的推理路径。
- 粒子滤波的观测 \(o_t\) 对应了思维链推理来自验证器(Verifier)或奖励模型(Reward Model)的反馈。
- 粒子滤波的权重 \(w_t\) 对应了思维链推理当前路径的可信度或置信度。
但,上面 CoT 原文独立采样 \(N\) 条思维链 \(z^{(1)}, \dots, z^{(N)}\),然后对答案 \(y\) 进行投票(Marginalization)。这导致了其没有序列的概念,如果第一步错了,整个链条就浪费了,不存在重采样等修正机制。
Tree of Thoughts: Deliberate Problem Solving with Large Language Models
2023 年的思维树论文思想类似于 \(A^*\) 算法,在每个思维步骤,生成多个候选分支。通过评估函数(Value Function)对分支评分,保留 Top-K 分支。
Sequential Monte Carlo Steering of Large Language Models using Probabilistic Programs
而这个 2023 年的论文相比于思维树,能够从错误的中间步骤中通过剔除进行恢复,并将计算集中在更有希望的推理路径上。
更具体的,其引入了粒子滤波的重采样思想,使用一个判别模型(Verifier)或自我反思(Self-Refine)来评估推理是否合理并赋予权重 \(w_t^{(i)}\)。随后,下一步推理开始前,根据权重进行重采样:丢弃那些逻辑错误的推理路径(低权重),复制那些逻辑严谨的路径(高权重)。
可以看到,思维链的优化越来越靠近粒子滤波的完整思想。也就是,人们开始将此逻辑生成过程转变为一个贝叶斯滤波问题,返璞归真。
视频生成与世界模型
粒子滤波的原始作用还是基于现实世界的物理时间进行下一步预测,而非思维链抽象的推理深度。
现代深度学习与时间最相关的当属 Sora,Vidu 等视频生成,还有 2025 年李飞飞、杨立昆等人推崇的世界模型,空间智能,与具身智能。
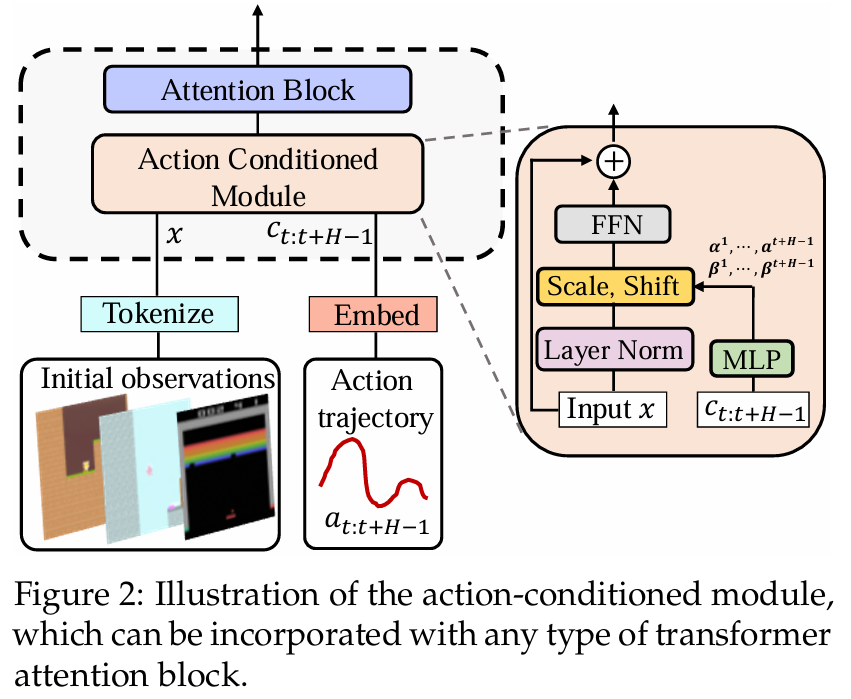
Pre-Trained Video Generative Models as World Simulators
关于上面两者的关系,这篇 2025 年的论文就试图将视频生成理解为世界模拟器。
他们提出了名为 DWS(Dynamic World Simulation) 的框架,包括了上面的两个模块:
- Lightweight Universal Action-Conditioned Module,通过两个线性层将动作信号注入到预训练网络中。
- Motion-Reinforced Training,强制模型重新分配注意力,使其更加关注动态区域和动作引起的转换,而非静态背景的细节。
也就是,通过简单的注入将视频与基于物理的动作关联起来,显式的让生成出来的视频拟合物理动作并符合物理规则。
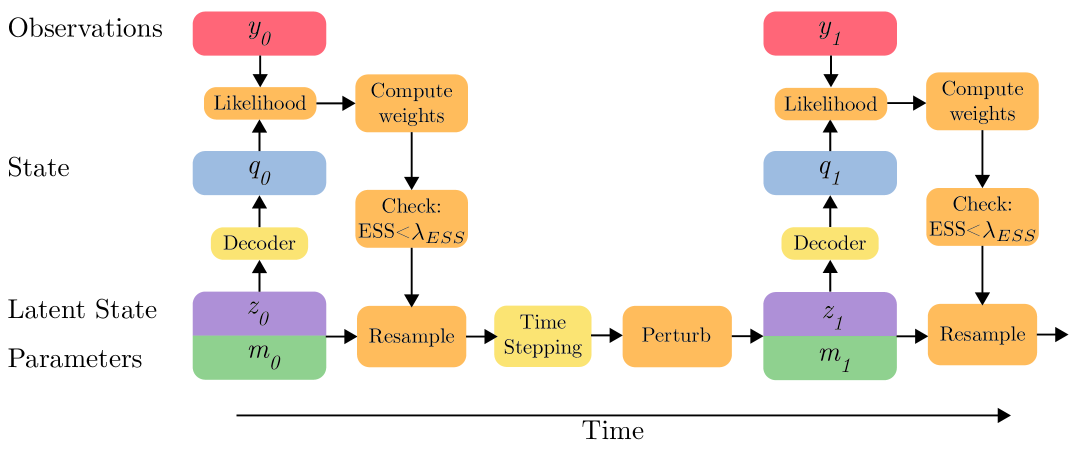
而这篇 2024 年的论文,尝试将粒子滤波直接应用到视频帧序列生成。
更具体的,由于像素空间极其高维,粒子滤波无法直接使用。为此,通过变分自编码器(VAE)的思想,先将视频帧映射到低维潜在空间,然后在潜在空间中,通过 Transformer 作为状态转移函数(Transition Model),利用粒子滤波算法来追踪潜在状态分布 \(p(z_t | z_{0:t-1})\)。
与确定性的 RNN 或 Transformer 相比,粒子滤波能更好地处理多模态不确定性(Multimodal Uncertainty)。如,当一个物体被遮挡后,它可能从左边出来,也可能从右边出来。粒子滤波可以用不同的粒子群同时表示这两种可能性,直到观测数据消除了歧义。可以发现,这种处理不确定性的能力对于生成符合物理规律的视频至关重要。
小结
可以看到,粒子滤波不仅序列蒙特卡洛思想一致活跃在学术界,其加权重采样也仍有一席之地。在语言模型中,它将单步的 System 1 直觉生成转化为多步的、可回溯的、基于概率权重的 System 2 思维链搜索,并通过重采样机制修正逻辑谬误;而在视频生成中,它利用潜在空间的序列蒙特卡洛采样,解决了高维像素空间中物理动态的不确定性问题。
也就是,无论是文本还是视频,粒子滤波都提供了一个统一的框架:在充满不确定性的动态系统中,通过不断的观测与加权,收敛至最优的真实状态。
总结
综上,这些最新论文全部验证了本文一开始的观点:经典理论并未过时。相反,随着模型规模的扩大,高维空间中的统计规律(如双重下降、良性过拟合)反而让经典理论(如间隔理论、流形假设)在解释性和指导性上变得更加有力;此外,在算力十分受限的今天,LoRA-XS、SageAttention 和 MoE 的成功证明,基于 PCA 和稀疏编码的“降维”与“稀疏化”是实现高效智能的必经之路;最后,粒子滤波在 CoT 和世界模型中的应用表明,下一代人工智能的核心竞争力将不再仅是静态知识的存储(记忆),而是动态逻辑的推演与对物理世界的概率模拟(推理)。