深度神经网络
什么是深度学习
神经元模型与神经网络
神经网络的优化
卷积神经网络 CNN
循环神经网络 RNN
2025年如唐杰教授所说，人工智能 AI 几乎等同于多模态大语言模型 LLM。也就是，目前的智能很大一部分归功于谷歌的 Transformer 架构和 Attention 注意力机制；还有最底层的，深度神经网络。
本文讨论注意力机制前的深度学习（深度神经网络），虽然确实很多细节，如BP推导现在 PyTorch，TensorFlow 都完美支持根本不需要自己来，但了解一下还是十分有必要的。
（基于朱军老师的PPT）
机器学习与深度学习
根据 Hinton 等人的定义，深度学习是基于人工神经网络的特征学习机器学习算法。这里的深度指的是人工神经网络层数的深。
这节将会讨论深度学习相比于机器学习的优势，以及深度学习（作为黑盒模型）如何解释与理解。
机器学习的问题
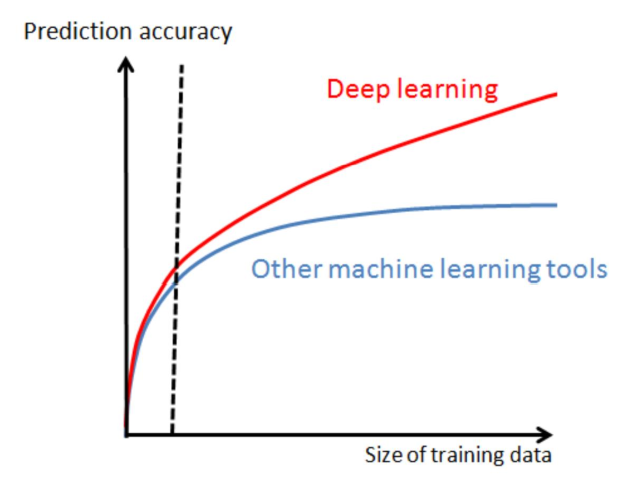
在传统机器学习时代，由于计算机算力限制，模型数据量往往不大。数据量不够的时候，机器学习算法往往过拟合（关注噪声），需要通过降低模型复杂度、容量来防止过拟合。
随着硬件的进步，现在大数据时代最不缺的就是数据。当数据量大、过于复杂时，机器学习算法往往无法拟合这么复杂的函数导致欠拟合，为了解决欠拟合，模型复杂度、容量往往需要提高的很多，这也导致了随之而来的优化和计算问题。
一会就可以看到，为什么深度学习模型的出现，解决了传统机器学习这一大痛点，完美贴合大数据时代的需求。
深度学习的统治力
众所周知，深度学习一经问世就展现了无敌的统治力。ImageNet 2013 物品检测竞赛人工特征还能勉强压深度学习一头、第二年的 ImageNet 2014 就彻底被深度学习碾压了。
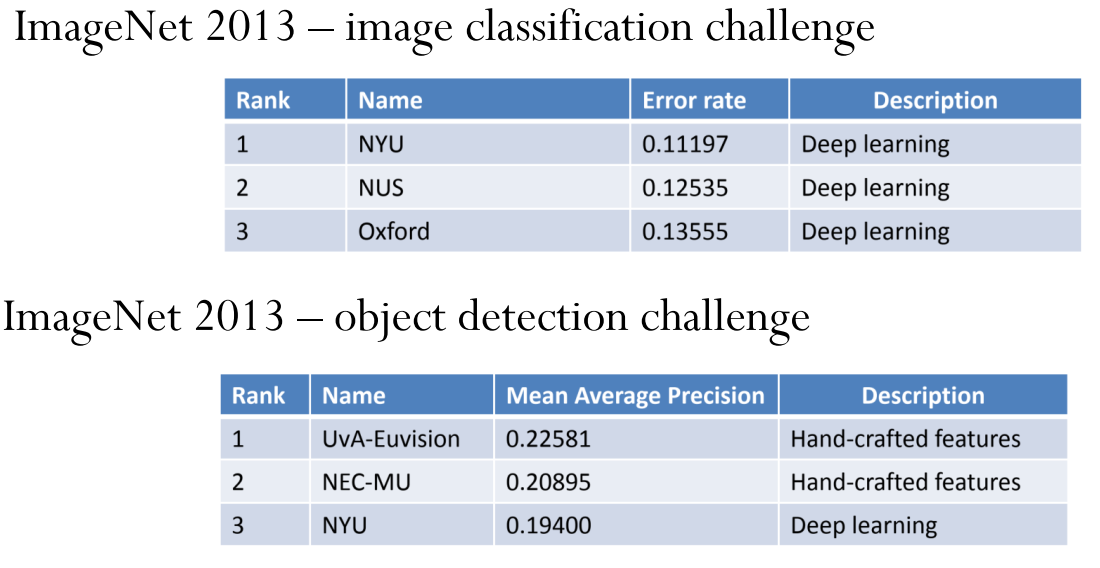
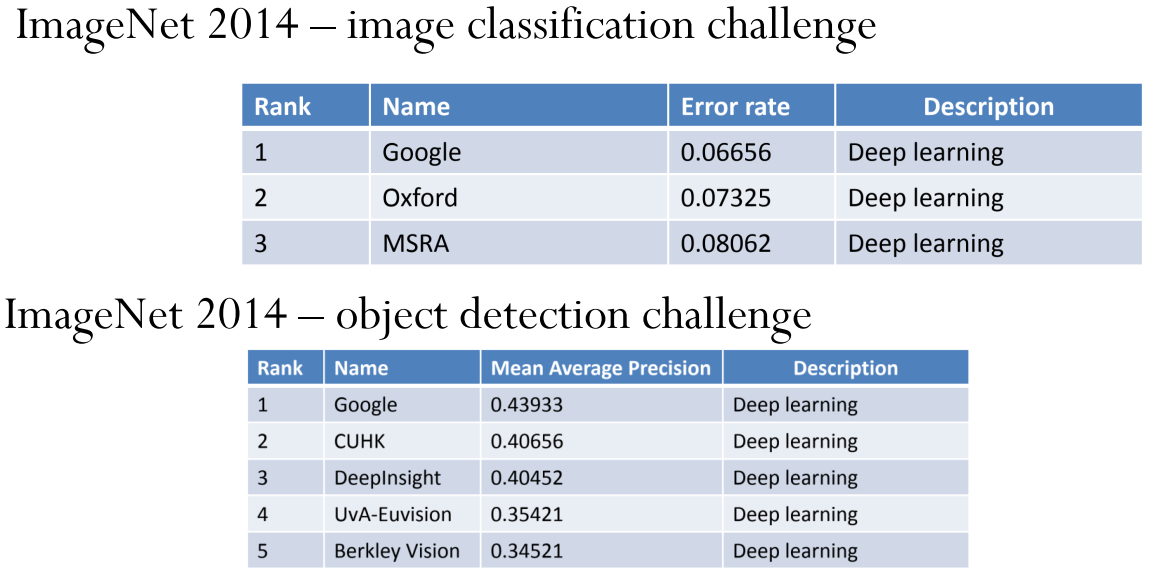
从上面两张图片和这篇文章最后面的表格：
机器学习的学习规则 - alittlebear’s blog
仅可以看到上述的统治力是有监督学习内的统治力。不过，
深度学习是如何统治所有机器学习的学习类型的 - alittlebear’s blog
这篇文章可以看出现在的深度学习模型（尤其是生成式模型）从 Transformer 的注意力机制开始，统治了机器学习领域的各个需求和任务。
深度学习规模化的优势
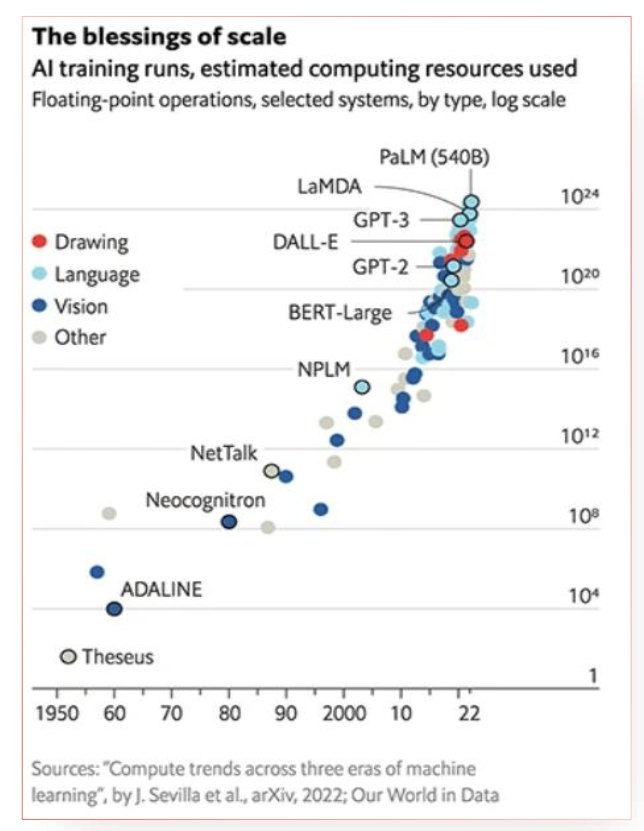
可以看到深度学习的进步都是尝试让模型越来越大（参数越来越多）。从结果来看，对于深度学习，难的题目往往比简单的题目更容易解决，i.e.，通过大数据与大网络训练出来的结果比小数据与小网络好很多。这也被称为“规模的红利”。
在注意力机制的大语言模型也有类似效应：
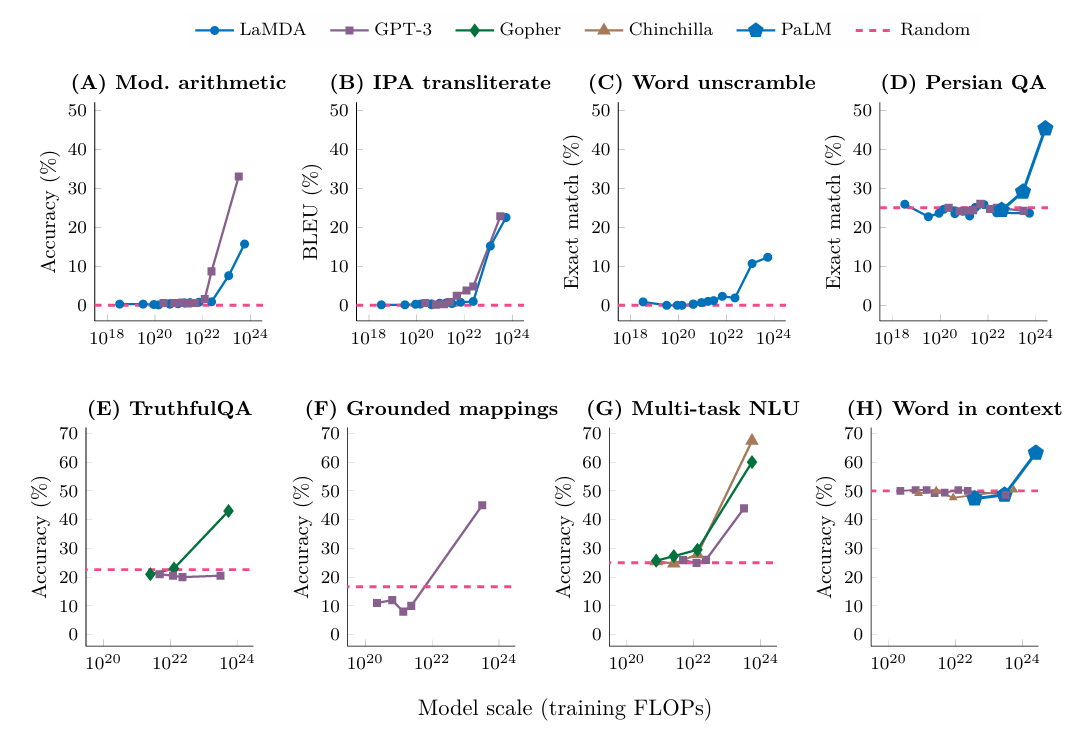
如这篇文章所说：Emergent Abilities of Large Language Models
对于所有大语言模型，当参数量达到一个数量级，其各种正确率飙升，也就是产生出所谓的涌现能力。
涌现能力：当一个复杂系统由许多微小个体构成时，这些微小个体在数量足够多时，能够在宏观层面上展现出微观个体无法解释的特殊现象。
深度学习特征提取的能力
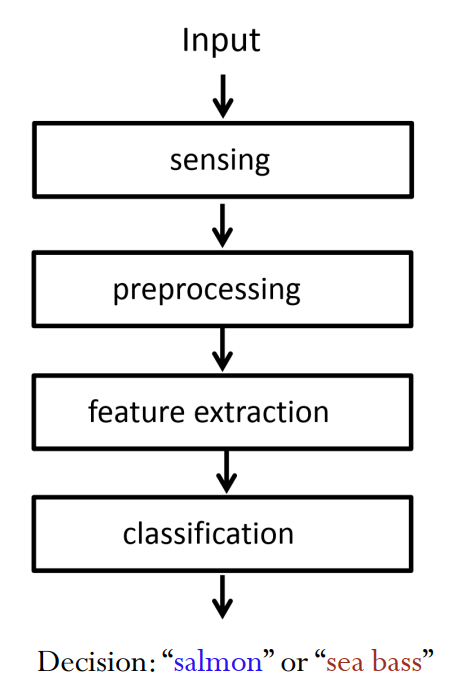
对于一个识别任务（三文鱼和海鲈鱼），传统的流程如上图所示是
\[输入\to感知\to预处理\to特征提取\to分类\]
但是人工进行的预处理和特征处理往往不是最优的、并且会丢失信息，导致分类模型获取到的信息减少。
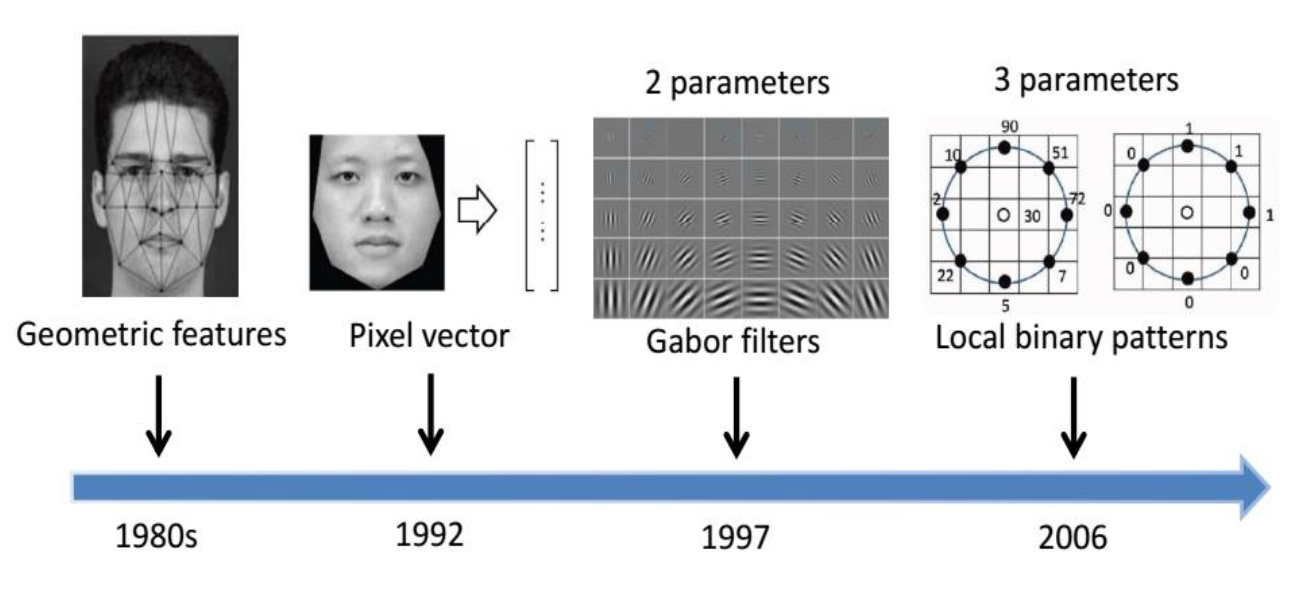
上图是人脸识别的人工选择的特征，可以看到一直在演变，并且无最优特征。
上图是图像特征工程的一些难题，如光照、变形、遮挡、背景干扰、类内差异。可以看到人很难设计出鲁棒（robust）的能够应对所有这些问题的特征提取方法。
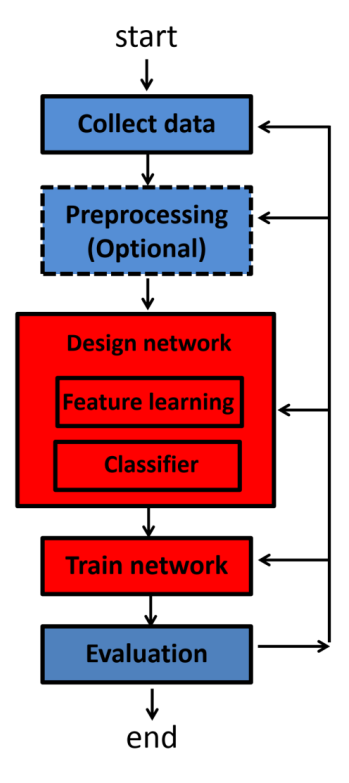
于是，这个任务除了刚开始的收集数据，和最后的评估可以用传统的方式，其他关于特征提取，分类，都可以用深度学习来代替了（上图红色部分）。数据预处理也甚至是没有必要的，因为预处理如之前提到的会丢失部分信息。
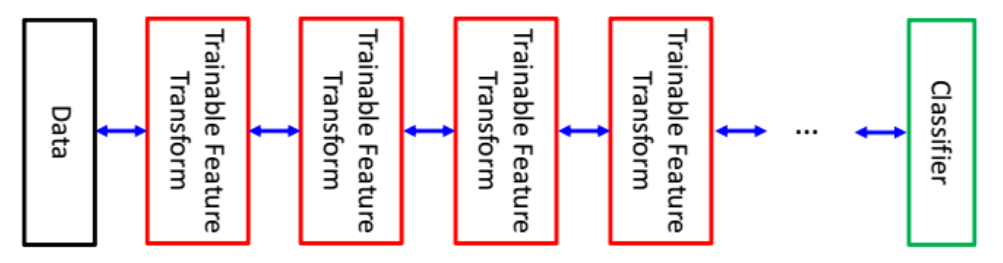
深度学习等于（融合在一起的）学习分层表示
基于以上思想，可以看出：
\[ 深度学习 = 整个机器都可以被训练 \]
也就是深度学习让机器学习从完成某个具体的分工变成完成整个任务（也被称为端到端学习 End-to-End Learning）。
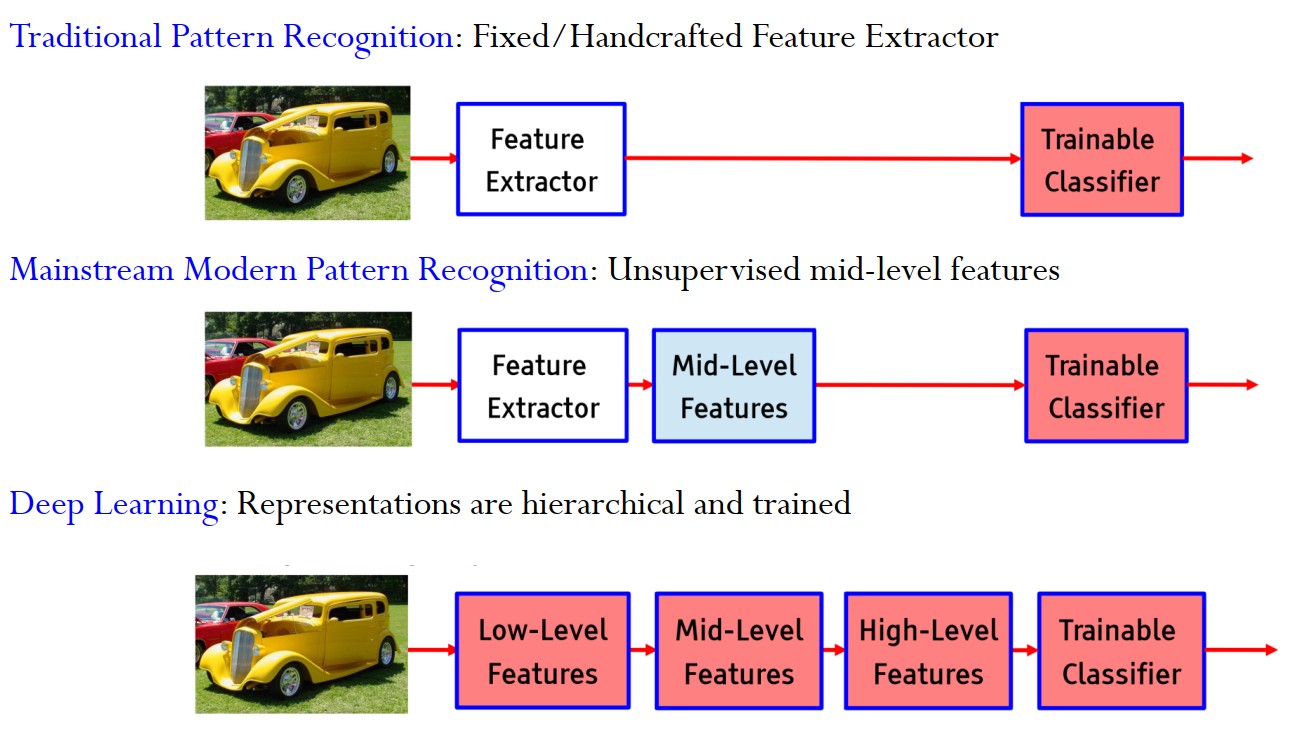
如考虑前面三文鱼和海鲈鱼，传统的机器学习仅完成分类这个步骤；而深度学习可以从原始数据提取底层信息、中层信息、高层信息、并且将他们作为特征进行分类，给出分类结果。
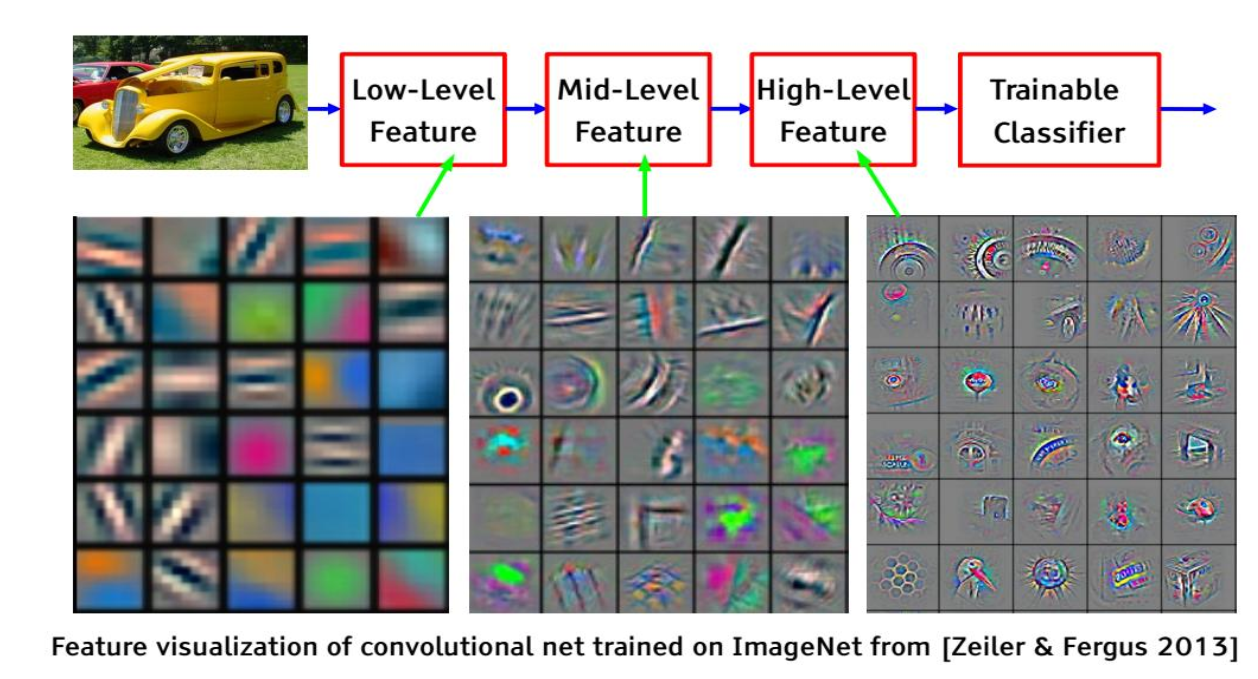
换句话说，深度学习就是（非线性的、融合在一起的）学习分层的特征表示，并且抽象程度逐层增加。
对于图像，分层特征可以是
\[ 像素\to 边缘\to 纹理基元\text{ Texton} \to 图样\text{ Motif}\to 局部\text{ Port}\to 物体\text{ Object}\]
对于文字，分层特征可以是
\[ 字符\to 词\to 短语\to 分句\to 句子\to 篇章\]
什么是好的深度学习特征
独立可解释的特征
正如人工特征一样，人们喜欢的往往是彼此独立不纠缠在一起的（可解释的）特征、因子。但在复杂情况很难给出这么一组（独立、可解释的）特征。
黑盒模型的定义就是提取特征的不可解释性，所以可以看到这就是为什么现在将深度学习称之为黑盒模型。
特征之间的不独立性是导致特征不可解释的主要原因之一。
如，对于人脸识别，深度学习提取的特征不是鼻子、眼睛、嘴巴、脸型的特征；每个特征可能不同部位彼此融合，人类无法解读。
此外，正如现实中人脑神经元的激活方式一样，一个概念通常是由多个神经元的组合激活来编码的（也许存在深层的相关性，或者是为了压缩网络参数数量）。也就是，一个神经元往往对应的不是某个特定的概念，可能会分别被“猫”、“毛毯”、“羽绒服”这些感觉上几乎不相关的概念激活。
综上，可以说目前的深度学习提取特征的方式（通过大数据、损失函数、和优化算法）和人类不一样，不只是方式不一样，还是数量级上的不一样。各方面导致了人类越来越无法理解（抽象的相关性、人脑无法处理的数量级）现在的深度学习模型。这里说得不一样是认知上的不一样，而不是和人脑处理方式的不一样。
并且，由于现在的深度学习将特征提取（升维）和后续处理（降维）完全的融合在了一起，对于一个神经元，人类连区分它是提取特征还是处理输入空间都做不到，更别谈研究提取的特征了。
流形假设
既然我们很难让深度学习模型学习到人类可以理解的特征，那么我们就尝试让模型尽量的去拟合输入数据分布。
流形假设（Manifold Hypothesis）假设了 自然 数据分布是嵌入输入空间的 低维 流行。
例子
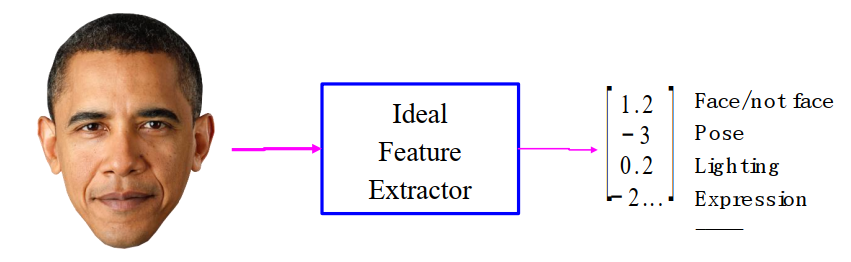
考虑 \(1000\times 1000=100,0000\) 像素的脸部图片输入，输入空间的维度是一百万。
但是，从各个角度都能看出人脸的长成根本不需要一百万个基元素：人脸可以由 3 个笛卡尔坐标、3 个欧拉角、和大约 50 个脸部肌肉描述。也就是，脸部图像的流行维度小于 56。
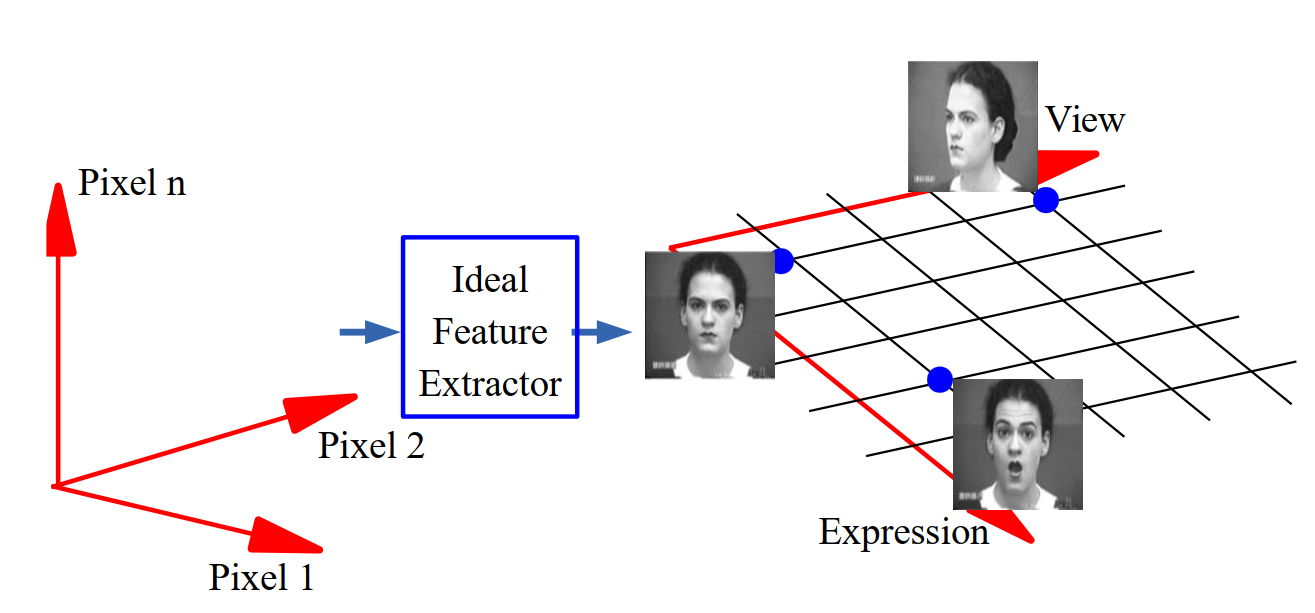
对于理想特征，正如上小节说的，我们希望特征彼此独立（不纠缠）。
特征的提取
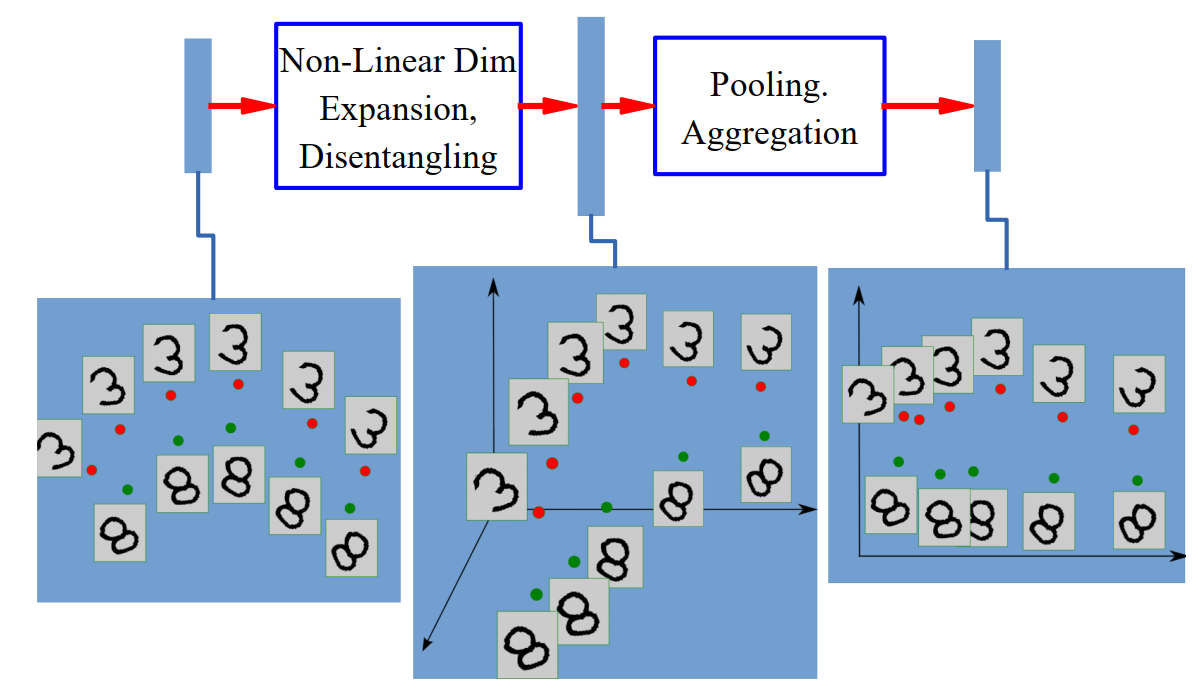
和 SVM - alittlebear’s blog 中核函数的目标一样，假设给定输入并不是以独立不纠缠特征方式给出的，为了转换成这种形式（便于模型后续处理）我们可以将输入通过非线性函数嵌入到高维空间来解除输入维度之间的纠缠。然后，通过池化，聚合等降维方式转换为不纠缠的（稳定、不变特征下的）低维表达。
神经元模型与神经网络架构
生物学上的神经元
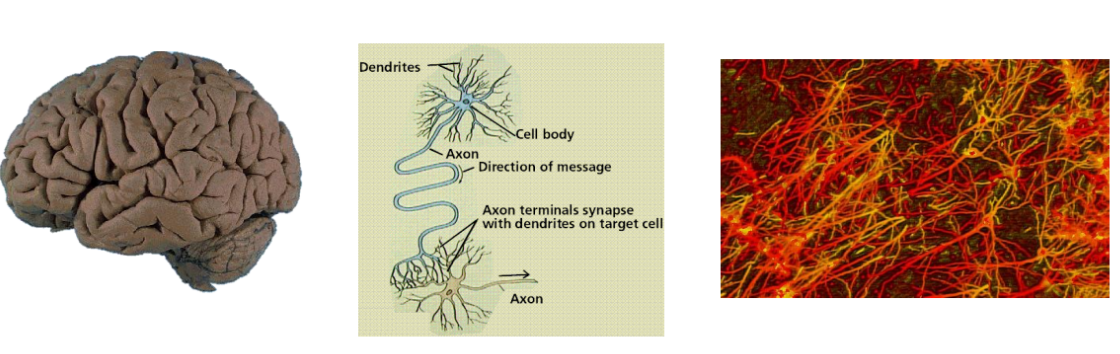
人类大脑是由一个个神经元通过突触（Synapses）连接而成的网络。学习本质上就是（通过NMDA受体）改变一个神经元对另一个的影响。
正如 Huber 和 Wiesel 在 1962 指出，大脑的视觉皮层存在层级结构：
- 简单细胞（Simple cells）检测局部特征。
- 复杂细胞（Complex cells）在视网膜拓扑领域内“池化（pooling）”。
McCulloch 和 Pitts 的人工神经元模型
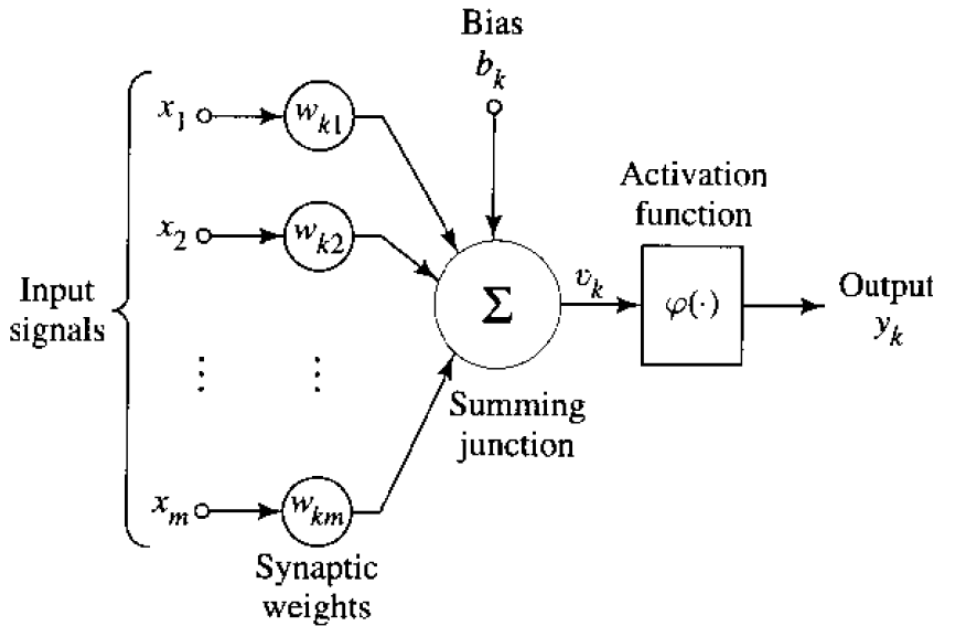
在1943年，McCulloch 和 Pitts 提出了最早的人工神经元模型。
如上图所示，一个神经元接收输入\(x=(x_1,...,x_m)\)，给每个输入 \(x_i\) 一个权重 \(w_i\)，加上一个偏置 \(b_k\)，最后通过激活函数 \(\varphi(\cdot)\) 输出结果 \[ y_k = \varphi\left(\sum_{j=1}^{m} w_{kj}x_j + b_k\right) \] 这里他们用的激活函数是符号函数 \(\varphi=\text{sgn}\)。
其他激活函数如下图所示，包括从最简单的符号函数到 Sigmoid 类型函数（激活函数和损失函数 - alittlebear’s blog）。
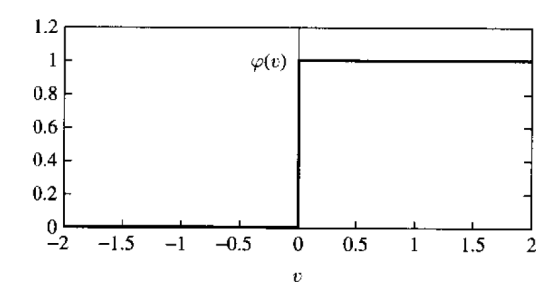
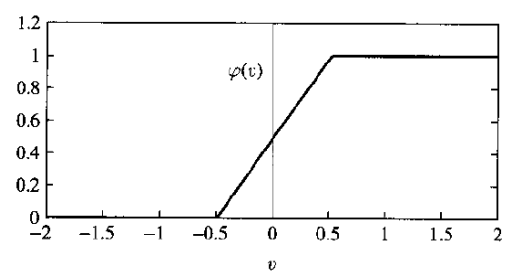
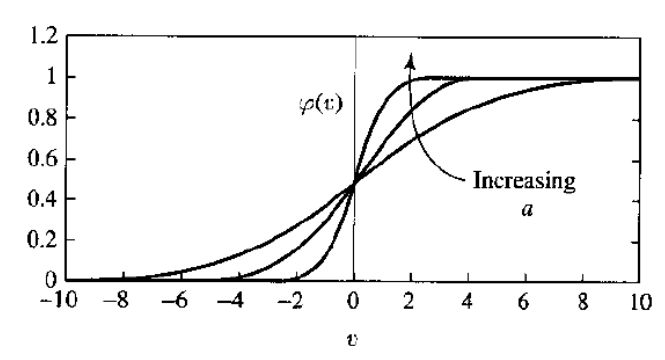
其中最后一图 \[ \phi_\alpha(v)=\frac1{1+\exp(-\alpha v)} \] Perceptrons: An Introduction to Computational Geometry | Books Gateway | MIT Press
Minsky 和 Papert 在 1969 的书 Perceptrons 证明了由输入和输出组成的单层感知机本质上还是线性模型（广义线性模型，可以参考生成式模型、判别式模型、指数族分布、和广义线性模型 - alittlebear’s blog）。
不过，后来衍生出的深层模型多层感知机（Multi-layer perceptron, MLP）根据万能函数拟合定理被证明出可以拟合任何非线性连续函数。加上BP算法的应用（本文后面会解释），让这一模型概念焕发新春。
神经网络结构
神经网络，由神经元组成的（多层感知机）网络，基本可以分为两种：
前馈神经网络 Feedforward Network
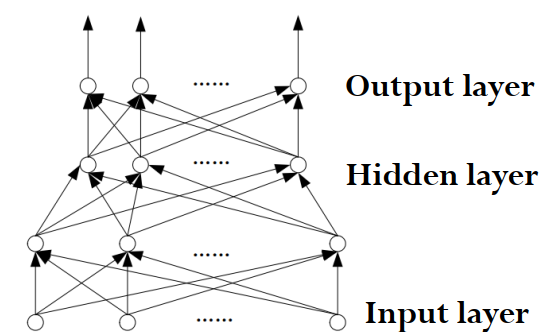
前馈神经网络可以看作是神经元模型的网络拓展。每个神经元都是将（上一层的部分或全部神经元作为）输入给予不同权重，然后激活函数输出。
可以看出信息流向是单向的，并且是分层的：从输入层到隐藏层，最后到输出层。
用之前的语言，也可以将这种层风描述为对于不同层次的特征提取，从底层到高层，最后用这些特征进行判断（分类、回归）并输出。当然，网络并没有明确每一层，每一个神经元的行为，所有行为都被融合在一起了。
循环神经网络 Recurrent Network
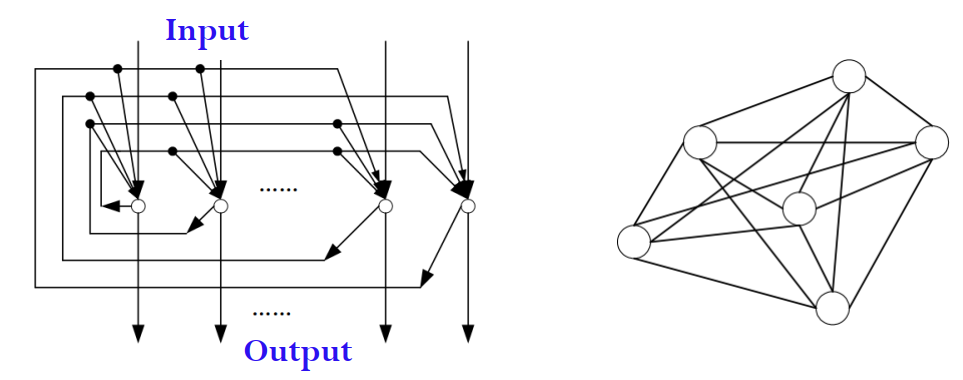
为了处理序列数据（sequence data）相邻数据的相关性，也就是，让前面的输出作为模型“权重、参数”的一部分，网络需要具备记忆能力。
为此，循环神经网络将上一时刻的输出结合这一时刻的输入，一起计算出这一时刻的输出。
具体细节本文最后会给出。
通用近似定理（Universal Approximation Theorem）
Kolmogorov-Arnold 表示定理 / 叠加定理
1957 年，Kolmogorov 的学生 Arnold 为了解决希尔伯特第 13 问题（某些多元函数无法还原为二元函数的组合），证明了 \[ f(x_1, \dots, x_n) = \sum_{q=0}^{2n} \Phi_q \left( \sum_{p=1}^n \psi_{q,p}(x_p) \right) \] 任何 \(n\) 元连续函数 \(f:[0,1]^n\to\R\) 都可以表示为有限个单变量连续函数的叠加。
可以看到理论上任何多元连续函数都可以被某个双层神经网络（并且仅需 \(2n+1\) 个隐藏单元）精确 表示，但激活函数极度依赖于目标函数 \(f\)，而且不固定，无法参数化，不能通过梯度下降等算法来学习这些激活函数。
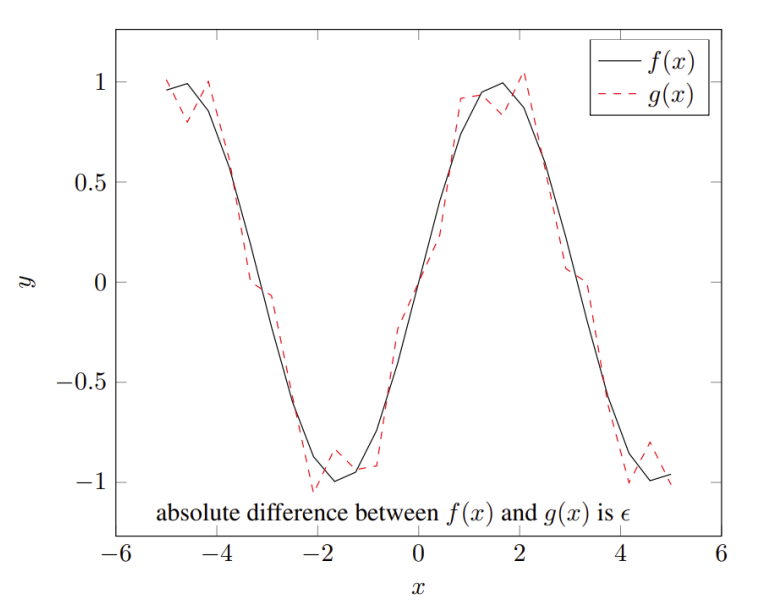
用 Sigmoidal 函数逼近叠加函数
1989 年，Cybenko 证明了任何多元连续函数不仅都可以被某个双层神经网络近似表示（误差任意小\(|f(x)-g(x)|<\varepsilon\)），所有激活函数还可以都是 Sigmoid 函数（也就是 Sigmoidal） （Logit, Logistic, Sigmoid, Softmax在MLP的区别 - alittlebear’s blog） \[ g(x) = \sum_{j=1}^{N} \alpha_j \sigma(y_j^T x + \theta_j) \] 其中 \(\sigma\) 是一个 Sigmoid 函数。\(N\)可以看作是隐藏层神经元数量（随着逼近精度要求变高，\(N\)可能趋近正无穷）。这里的证明用到了泛函分析的 Hahn-Banach Theorem 和 Riesz Representation Theorem。
虽然现在是近似而不是精确表示，不过起码激活函数都固定下来了，这样就有了神经网络“学习”任何多元连续函数的可能，如梯度下降。
用任意非多项式函数逼近
Leshno 等人在 1993 年的论文《Multilayer Feedforward Networks With a Nonpolynomial Activation Function Can Approximate Any Function》证明，只要激活函数 \(\sigma\) 不是多项式，它就能成为通用逼近器（用来逼近任何多元连续函数）。
更具体的， 设 \(\sigma\) 是局部黎曼可积函数。由 \(\sigma\) 构建的单隐层网络在连续函数空间中稠密的充要条件是 \(\sigma\) 不是几乎处处为多项式。
用 ReLU 激活函数逼近
The Expressive Power of Neural Networks: A View from the Width
Lu 等人在 2017 年对 ReLU 激活函数的神经网络的逼近证明了更低的宽度上界。对于任何 Lebesgue 可积函数 \(f:\mathbb{R}^n\to\mathbb{R}\) 和任意小 \(\varepsilon >0\)，存在宽度 \(d_m\le n+4\) 的全链接 ReLU 网络，并且总逼近误差小于 \(\varepsilon\)： \[ \int_{\mathbb{R}^n}|f(x)-F_A(x)|\text{d}x<\varepsilon \] Sigmoidal 平滑的叠加类似于傅里叶变化，而用如 ReLU（激活函数和损失函数 - alittlebear’s blog）叠加可以看作是用一段段直线、三角来近似。
网络应该窄而深还是宽而浅
上一小节的通用近似定理证明了理论上一层隐藏层的神经网络就足够拟合任何多元连续函数，但并没有证明这么做最高效。
The Power of Depth for Feedforward Neural Networks
Eldan 和 Shamir 在 2016 证明了存在某些函数，可以被小的三层前馈神经网络逼近表示，但相同逼近精度的二层网络需要指数级的宽度增加。
所以，增加网络的深度（层数）通常比增加宽度（单层神经元数量）更能提高性能和效率。
或者是宽而深！？（过参数化）
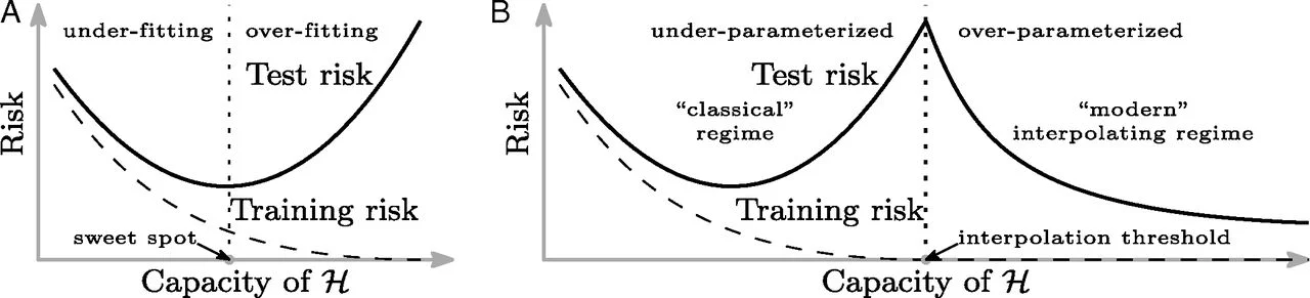
模型复杂度的双重下降（Double Descent）
Reconciling modern machine-learning practice and the classical bias–variance trade-off | PNAS
Belkin 等人在 2019 年提出了“双重下降”这个概念，并提出传统机器学习的U型曲线仅适用于欠参数化（under-parametrized）的模型。
在传统机器学习和统计学中，测试误差往往对模型复杂度呈现U型曲线：欠拟合（模型复杂度过低、容量过小；记不住数据的基本特征）、拟合的刚好、过拟合（模型复杂度过高、容量太大；数据的噪声影响过大）。
但如上图右边所示，在现代深度学习大模型中，观测到了测试误差在过拟合后会再次下降甚至优于传统的最优点。随着参数（模型容量、复杂度）的增加也分为三个阶段：U型曲线阶段、测试误差最高的临界点（噪音影响最大）、在这之后随着参数量的增加，测试误差重新下降。
Surprises in High-Dimensional Ridgeless Least Squares Interpolation
Hastie 等人同年证明了对于线性回归模型，参数数量 \(p\) 与样本数量 \(n\) 的比值 \(\gamma = p/n \approx 1\) 时，方差会趋向无穷大（因为求逆矩阵变得极不稳定）。也就是，\(p=n\) 是临界点。
（现代大）模型各方面的双重下降
Deep Double Descent: Where Bigger Models and More Data Hurt
OpenAI 在同年将 Belkin 等人的理论从线性模型推广到了现代深层神经网络（CNN，Transformer），并发现不仅在“模型容量（模型复杂度、大小）”这个概念有双重下降这个现象，在网络深度、宽度、训练轮数（Epoch）各个方面都出现了双重下降。
并且，OpenAI 还发现了对于处于测试误差（最高）临界点的模型，增加数据（噪声）只会让模型的泛化能力（测试误差）变得更差。
为什么存在双重下降
现代插值区间 Modern Interpolation Regime
基于双重下降这个现象，Belkin 等人在 2019 年还提出了现代插值区间这个概念：当模型大到足以记住所有训练数据时，它倾向于通过选择“范数最小”（Minimum Norm）的解来平滑函数，从而获得良好的泛化能力。
良性过拟合 Benign Overfitting
Benign Overfitting in Linear Regression
Bartlett 等人在 2020 年提出了良性过拟合来解释双重下降：即便模型完美拟合了噪声数据，如果多余的参数能让解的范数分布得足够“均匀”，那么噪声的影响就会被稀释。
顿悟现象
Grokking: Generalization Beyond Overfitting on Small Algorithmic Datasets
Power 等人在 2022 年提出了关于训练轮数（Epoch）双重下降的解释：随机梯度下降 SGD 在“记住数据”之后，还在暗中优化模型的内部结构以寻找更平滑的解。
可以看到，这种解释类似于人对人脑学习的理解，先死记硬背，然后尝试从中找出规律，然后记住规律，这样遗忘的时候会优先遗忘死记硬背的实际输入。
双重下降的总结
可以看到，目前的研究从很多角度都能解释（过参数化带来的）双重下降。我认为基本看法都是过参数化可以带来稀疏化和平滑化，而稀疏化和平滑化等同于提高泛化能力，所以过参数化等于泛化；此外，很多传统的机器学习算法是先将输入空间升维，分离，然后转换成低维形式的分离。这类似于用过参数化的网络先对数据进行很高维度的升维，然后通过梯度下降的方式慢慢进行降维（稀疏化）的同时保留分离出来的特征。
Weight-sparse transformers have interpretable circuits
可以看到 2025 年 OpenAI 也还在深入研究过参数化，或者说其带来的优势：稀疏化。
神经网络的训练与优化
误差修正学习
如这篇文章提到的：
机器学习的学习规则 - alittlebear’s blog
对于监督学习，我们可以用真实标签对模型进行调参，让错误率趋于 0。如以下格式 \[ Err(W)=\frac1T\sum_i div\left(f(x_i; W), y\right) \] 其中 \(Err\) 是平均错误率，\(div\) 是散度函数并且随着预测正确趋于 0。
由于复杂的神经网络往往没有闭式解（closed form solution），优化只能通过迭代的方式进行，如随机梯度下降。
生成式模型、判别式模型、指数族分布、和广义线性模型 - alittlebear’s blog
这篇文章的优化算法小结解释了为什么现在深度学习广泛使用的优化方法都是随机梯度下降。
但可以看到其中的结论“对于非凸函数，SGD一定收敛到局部最优”，神经网络往往不是凸函数，下一小节将解释为什么非凸的神经网络还是可以通过随机梯度下降来优化。
对于神经网络，SGD极大概率能下降到接近全局最大值
需要注意的是，一下结论基本对大型神经网络
绝大多数梯度为零的点为鞍点（Saddle points）
Identifying and attacking the saddle point problem in high-dimensional non-convex optimization
Bengio 等人在 2014 年就证明了绝大多数梯度为零的点为鞍点（某些方向是极小值，某些方向是极大值）。于是，就算优化到了鞍点，SGD 还是可以用噪声、冲量往是极大值的方向优化。
大部分局部最小值都接近全局最小值
The Loss Surfaces of Multilayer Networks
Choromanska 等人在 2015 年用统计物理中的自旋玻璃（Spin Glass）模型来解释神经网络，并得出结论：大部分局部极小值都非常接近全局最小值。
现代残差（Residual）网络结构让损失地形变几乎凸
Visualizing the Loss Landscape of Neural Nets
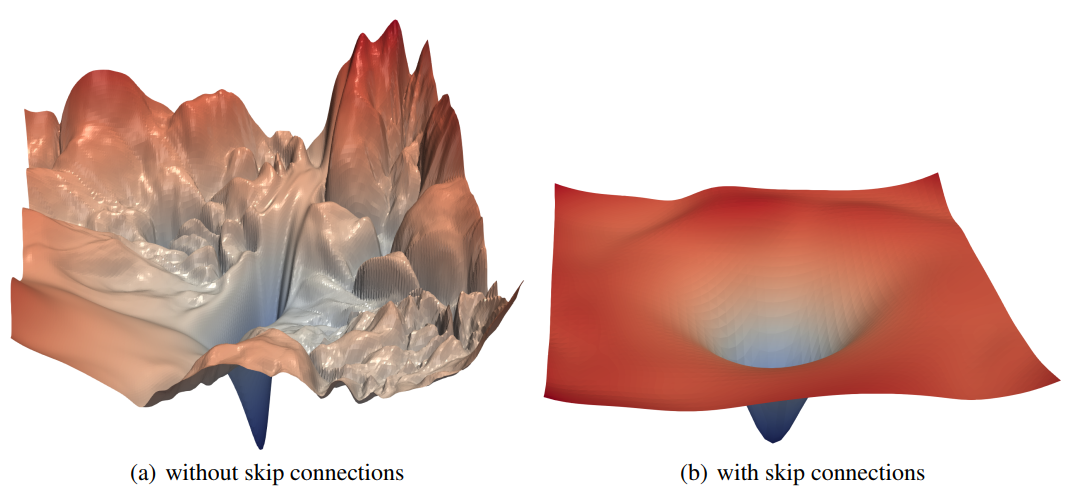
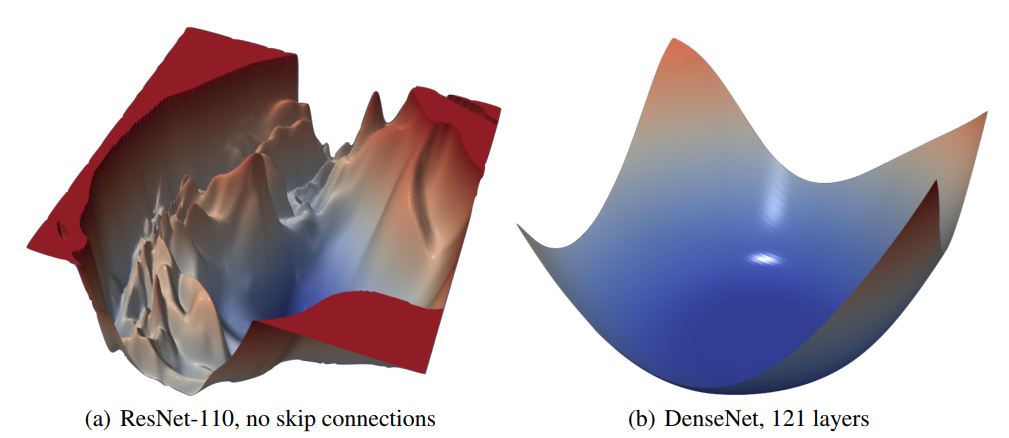
ResNet 和 DenseNet 的结构参考 从LeNet到DenseNet：Transformer前卷积神经网络的一些优化技巧/结构优化 - alittlebear’s blog
从 Li 等人 2018 年的工作可以看到，ResNet提出的跳跃链接（skip connection）让优化变得十分平滑，甚至对于有全部跳跃链接的DenseNet，损失函数基本是凸的。
最优解之间是连通的
Loss Surfaces, Mode Connectivity, and Fast Ensembling of DNNs
对于更普遍的模型， Garipov 等人在 2018 年发现在两个训练好的神经网络解之间，存在一条路径，路径高度不增加。也就是，“谷底”都是连在一起、想通的。
过参数化保证全局收敛
Gradient Descent Finds Global Minima of Deep Neural Networks
此外，对于现在过参数化的模型，Du 等人在 2019 年的研究进一步表明，当宽度\(m\to \infty\)时，损失函数表现出类似于凸优化的性质（满足 Polyak-Lojasiewicz 条件）。
小总结
可以看到现代神经网络从各个方面基本可以当作是凸函数（或者说对于梯度下降来说和凸函数无异），这为梯度下降提供了很强的理论支持。
现代模块化神经网络的误差反向传播算法（Back Propagation，BP）
上小节提出了神经网络可以用梯度下降来优化损失函数的可能性。但，对于一个多层网络，一次更新所有梯度从各个角度来看都是不现实的。
Learning representations by back-propagating errors | Nature
Hinton 等人在 1986 年提出了（误差）反向传播算法，从最后一层的梯度开始，通过链式法则一层一层，直到计算出第一层的梯度。
但梯度更新的顺序和计算输入的顺序完全相反。于是，这就构成了现代神经网络训练的前向传播（forward pass）和反向传播（backward pass）了。
前向传播就是用固定好的权重一层一层计算输入，并最终给出输出；接下要解释的反向传播就对应了上述的，从后向前，逐层计算梯度并更新权重。
正如 从LeNet到DenseNet：Transformer前卷积神经网络的一些优化技巧/结构优化 - alittlebear’s blog 这篇文章看到的，现在的神经网络（CNN，ViT，MoE，MultiModal）都是模块化的，本文将直接介绍模块化神经网络的反向传播 BP 算法，原理完全一样。
前向传播
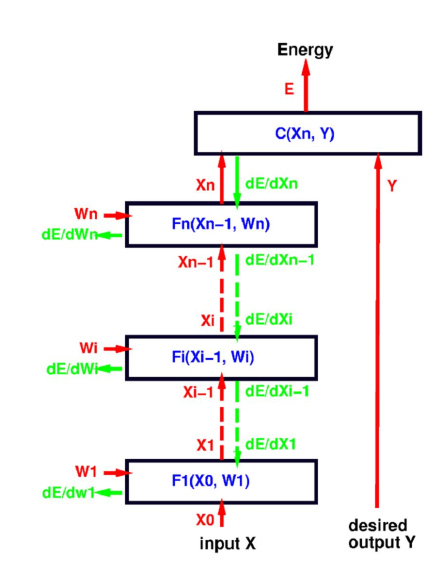
考虑上图的模块化神经网络。前向传播流程为：对于输入 \(X_0\)，第 \(i\in[1,n]\cap\mathbb{Z}\) 个模块计算 \(X_i=F_i(X_{i-1},W_i)\)，最终得到需要优化的函数 \(E(Y,X,W)=C(X_n,Y)\)。
反向传播
为了优化每个模块的权重矩阵 \(W_i\)，我们需要计算其对优化函数 \(E\) 的偏导。因网络的结构，我们可以从计算最后一层的偏导开始，逐渐用链式法则推到出前面的偏导，直到到达第一层。
因 \(X_k=F_k(X_{k-1},W_k)\)，替换一下得到 \[ \begin{align} \frac{\partial E}{\partial W_k} &= \frac{\partial E}{\partial X_k}\frac{\partial F_k(X_{k-1}, W_k)}{\partial W_k}\\ [1\times N_w]&=[1\times N_x]\cdot[N_x\times N_w]\\ \left[ \frac{\partial F_k(X_{k-1},W_k)}{\partial W_k} \right]_{ij} &= \frac{\partial [F_k(X_{k-1},W_k)]_i}{\partial [W_k]_j} \end{align} \] 于是，流程如下： \[ \begin{aligned} \frac{\partial E}{\partial X_n} &= \frac{\partial C(X_n,Y)}{\partial X_n} \\ \frac{\partial E}{\partial X_{n-1}} &= \frac{\partial E}{\partial X_n} \frac{\partial F_n(X_{n-1},W_n)}{\partial X_{n-1}} \\ \frac{\partial E}{\partial W_n} &= \frac{\partial E}{\partial X_n} \frac{\partial F_n(X_{n-1},W_n)}{\partial W_n} \\ \frac{\partial E}{\partial X_{n-2}} &= \frac{\partial E}{\partial X_{n-1}} \frac{\partial F_{n-1}(X_{n-2},W_{n-1})}{\partial X_{n-2}} \\ \frac{\partial E}{\partial W_{n-1}} &= \frac{\partial E}{\partial X_{n-1}} \frac{\partial F_{n-1}(X_{n-2},W_{n-1})}{\partial W_{n-1}} \end{aligned} \] 直到求出 \(\frac{\partial E}{\partial W_1}\)。
为了进行反向传播，可以看到在前向传播时我们需要保留所有中间输出 \(F_i\)。
反向传播的问题
可以看到，整个反向传播算法都是基于我们要优化的目标函数是损失函数（能量函数、代价函数），而这个函数不一定是真正最小化我们要的目标。
如对于分类任务，最小化散度不等于最小化分类错误。
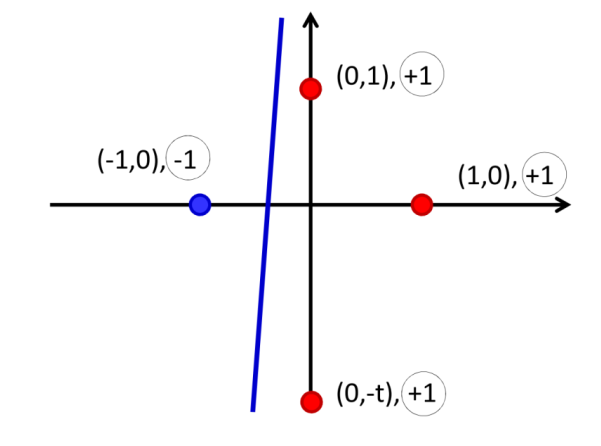
对于上图 \(t\to\infty\)
的情况，最下面这个红点几乎影响不到散度： \[
\frac{\partial div_4}{\partial w_y}=\frac{\partial div_4}{\partial
b}\to0
\] 
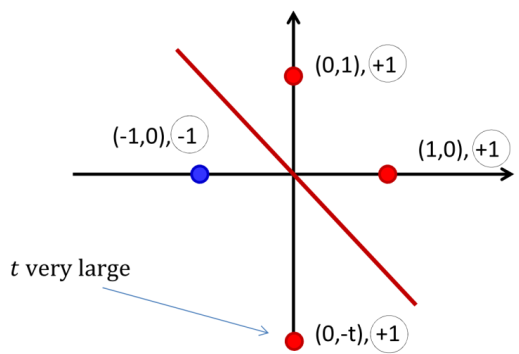
于是导致优化散度时最下面这个点会被分类错误。
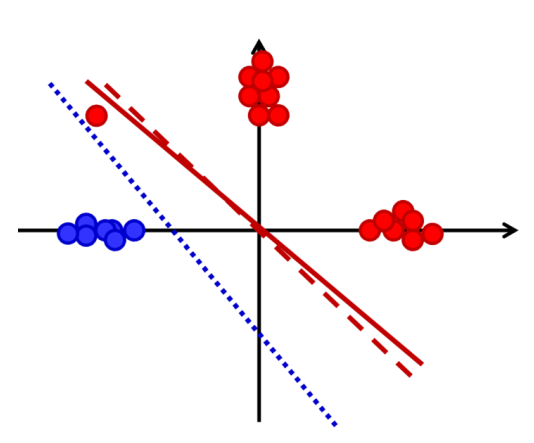
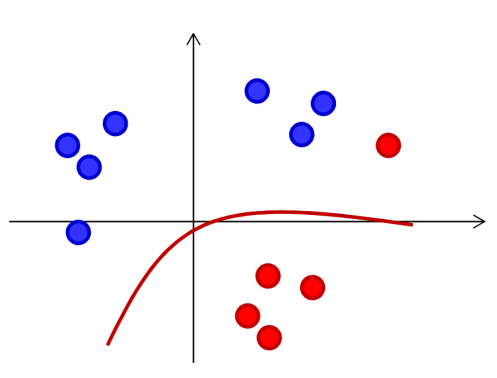
可以看到，BP 算法尽量保持方差（variance）低，但相应的偏见（Bias）可能会提高。Bias-Variance 参考 受AdaBoost启发的Margin Theory间隔理论 - alittlebear’s blog。
卷积神经网络（Convolutional NN，CNN）
卷积的概念
卷积核和池化
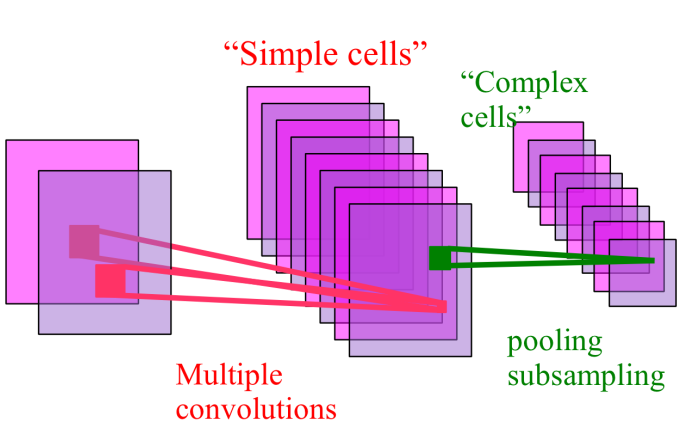
正如前面提到的，Hubel 和 Wiesel 在 1962 年发现了生物大脑中处理视觉的简单细胞（simple cells）和复杂细胞（complex cells）。
简单细胞检测局部特征、复杂细胞从数量庞大的简单细胞（池化的）提取信息。
基于这个概念，Lecun 等人在 1989 年基于 BP 设计了第一个卷积神经网络。
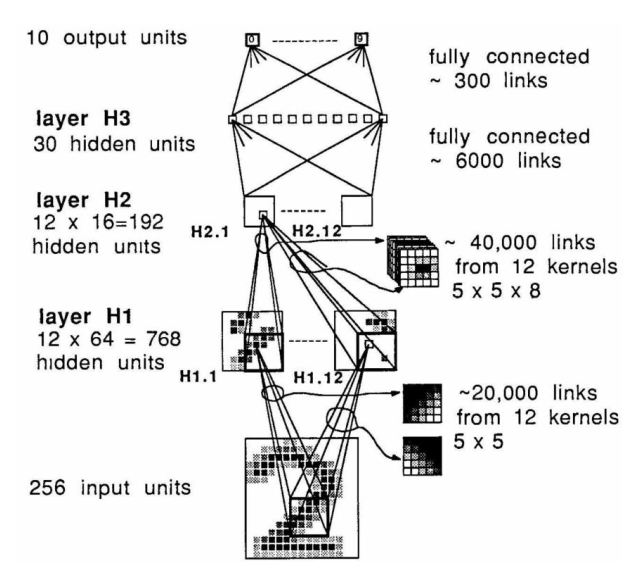
平移不变性
对于很多图像任务，如上图所示，目标的位置往往不重要，其特征更重要。
为此，对于相同特征我们需要对图像的每个截取都用 一样 的卷积网络来获取特征，并用（最大）池化（max pooling）来忽略细微抖动让模型变得更加鲁棒（robust）。对于不同特征，我们用不同的卷积核来提取，这些特征就对应了卷积神经网络中 通道 这个概念。
此外，虽然一个卷积核对图像每个截取权重都是相同的，在卷积神经网络里，对不同输入通道的权重是不同的。如，对于256通道的输入，\(3\times3\)大小的卷积核实际上使用了\(3\times3\times256\)个权重，并最终融合输出一个通道。
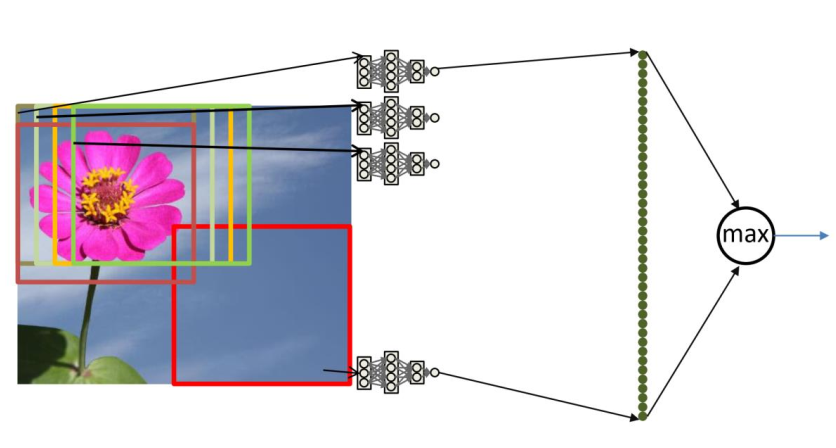
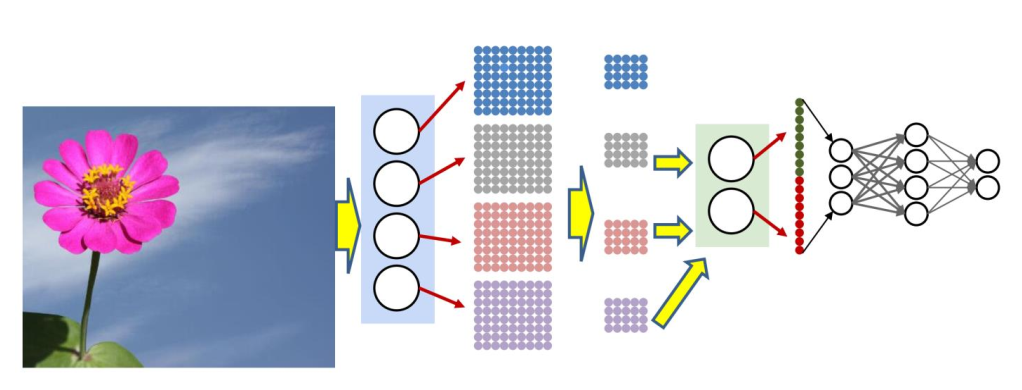
于是卷积神经网络整体的流程就变成了：卷积层、激活函数、池化、最后用MLP判断。
卷积模型发展
参考这篇文章：
从LeNet到DenseNet：Transformer前卷积神经网络的一些优化技巧/结构优化 - alittlebear’s blog
卷积神经网络的应用
现在和视觉相关的机器学习模型基本都用到了卷积核。
分类
检测
分割
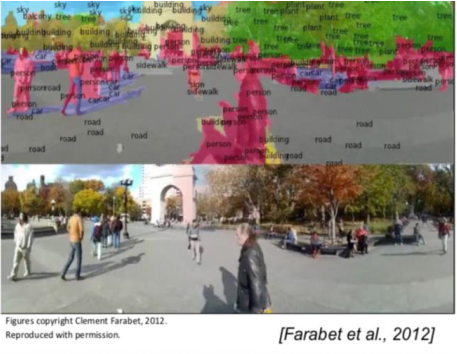
动作识别
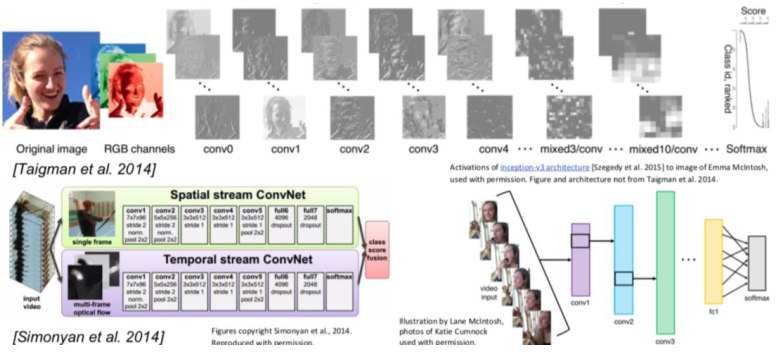
循环神经网络（Recurrent NN，RNN）
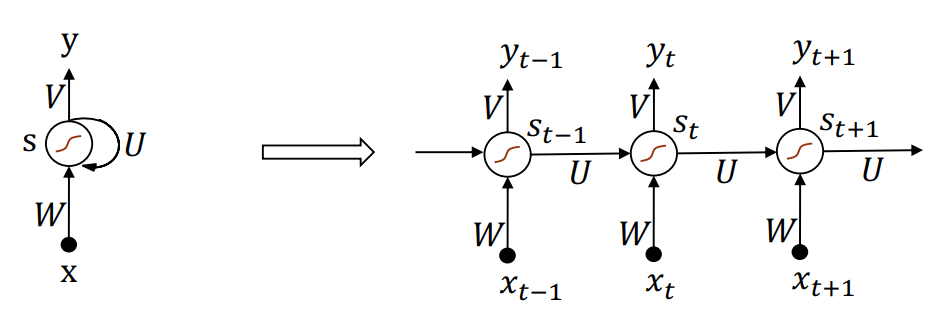
正如前文所说的，有时候数据（输出）之间不是独立的。对于输入，一句话的一个词需要上（下）文来理解，时序数据也需要前面的数据来判断；对于输出，想生成一句完整通顺的话必不可少的就是分析前面已经说的部分。
如，对于输入 \(s_0, s_1, ...\) 和输出 \(y_0, y_1, ...\) 上图的循环神经网络对每个输入 \(s_t\) ：用一组固定的权重 \(W\) ，前一个输入 \(s_{t-1}\) 通过权重矩阵 \(U\)，来用输出的权重矩阵 \(V\) 输出 \(y_t\)。
和在线学习的区别
这里的权重矩阵 \(U, W, V\)对不同时间的输入都是共享（固定）的。这和在线学习不同：在线学习的输入不一定是彼此有关联的，主要思想是每接收到一个样本就通过随机梯度下降 SGD 优化并更新权重，是一种（实时）训练方式。
而循环神经网络 RNN 与其说是在线学习不如说是在线推理（inference），推理阶段动态保存前一个输入来推理当前输入。
一对多（一对N）
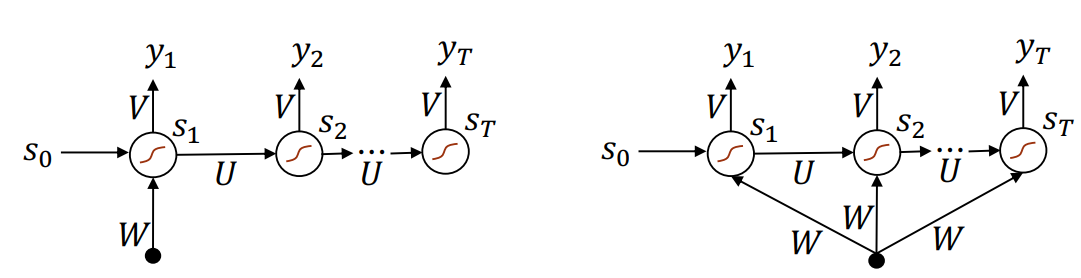
有时候我们的需求是给定输入 \(s_0\)，我们希望得到一系列彼此关联的输出 \(y_0, y_1, ...\)。如，给定一张图，我们希望模型生成一句话（词的序列）作为描述。
多对多（N对N）
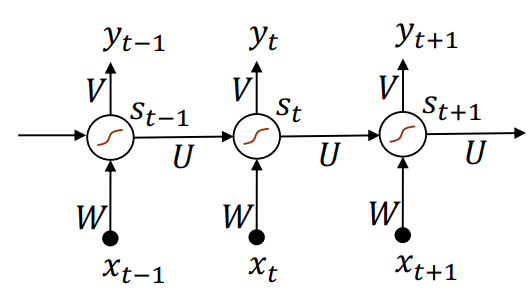
对应了本节开头举的例子。这种情况适合分析原有数据并进行批注，如对于词性标注的任务，这种 RNN 可以对句子中的每个词都生成一个标签。
多对多（N对M）
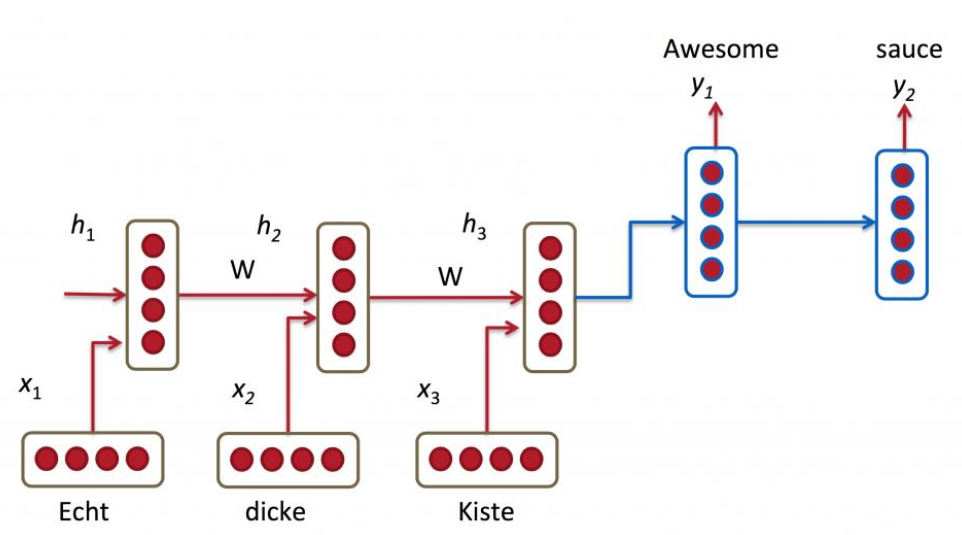
除了简单对句子每个词生成一个标签进行批注，我们也希望可以让模型可以完全理解整个句子，并生成出如一个新的句子。
这需求对应了机器翻译（machine translation），如中英互译。
这种某种意义上的“加密-解密”结构也被称为 Encoder-Decoder 模型。
RNN 的 BP 算法：随时间反向传播 （Backpropagation Through Time，BPTT）
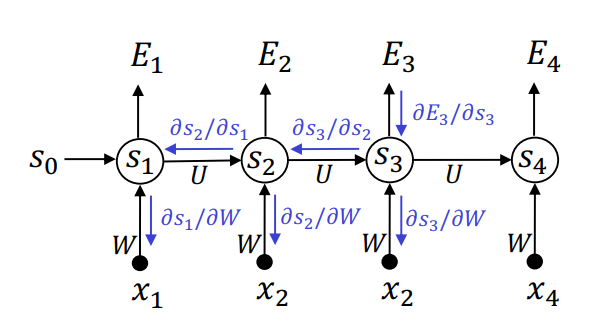
因为 RNN 的参数共享，想求出（上图）\(s_4\) 的损失函数 \(E_4\)，其对权重 \(W\) 的梯度依赖所有之前的输入 \(s_1, ..., s_3\)：
假设损失函数为交叉熵 \[ E_t = -y_t \log \hat{y}_t \] 那么偏导为 \[ \begin{aligned} \frac{\partial E_3}{\partial W} &= \frac{\partial E_3}{\partial \hat{y}_3} \frac{\partial \hat{y}_3}{\partial W} \\ &= \frac{\partial E_3}{\partial \hat{y}_3} \frac{\partial \hat{y}_3}{\partial s_3} \left( \frac{\partial s_3}{\partial W} + \frac{\partial s_3}{\partial s_2} \frac{\partial s_2}{\partial W} + \frac{\partial s_3}{\partial s_2} \frac{\partial s_2}{\partial s_1} \frac{\partial s_1}{\partial W} \right) \end{aligned} \] 可以看到，梯度在（经过超长距离的）反向传播回初始时刻时可能会指数级衰减，从而导致长输入的“梯度消失”。
更具体的，如果权重矩阵某些元素小于\(1\)，那么对于长度为 100 的时序序列输入，求梯度需要将这一数字乘上 100 次，最终结果极有可能几乎为 0。
为此，Graves 等人在 2009 年提出了下面的结构：LSTM。
长短期记忆模块（Long Short-Term Memory，LSTM）
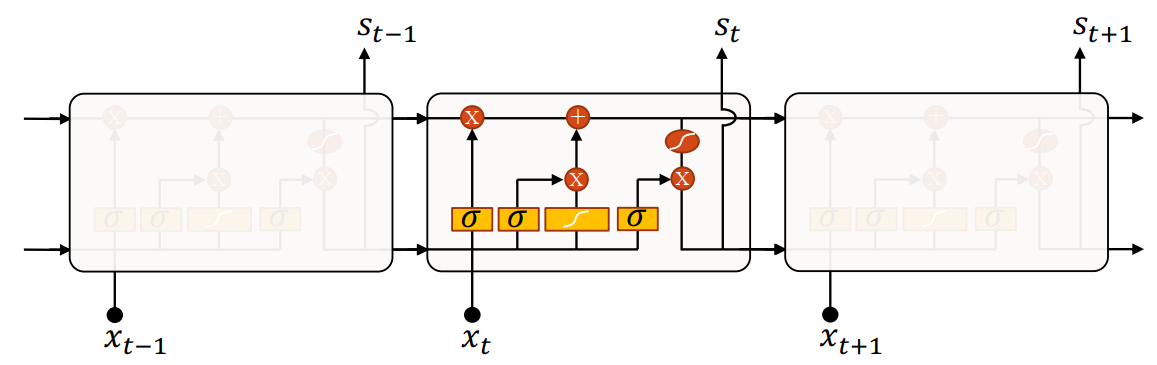
（图片来自 Graves 等人 2009 年的论文《A Novel Connectionist System for Improved Unconstrained Handwriting Recognition》）
如图，Graves 等人将原 RNN 网络的简单隐藏单元替换成了一个 LSTM 长短期记忆（神经网络）模块。
此模块“智能”的判断什么时候记忆输入、什么时候保持或遗忘记忆、什么时候输出。每个模块由三个门控制：遗忘门、输入门、输出门。每个门由 Sigmoid 函数 \(\sigma\) 控制：接近 0 代表遗忘、不记忆；接近 1 代表保留、记忆。每个门本质上都是一个单层感知机、全连接层，输出为固定超参数（单元数 units 、隐藏层维度 hidden size）。
并且，输入除了接收上一时刻的输出 \(s_{t-1}\)，还有一条（上方的）“传送带（细胞状态， cell state）” \(c_{t-1}\)，其保留了经过筛选的历史信息维度状态。\(c_{t-1}\) 作为一个向量，维度和门输出的维度一致（\(c_{t-1}\) 的维度从始至终保持一致）。
遗忘门
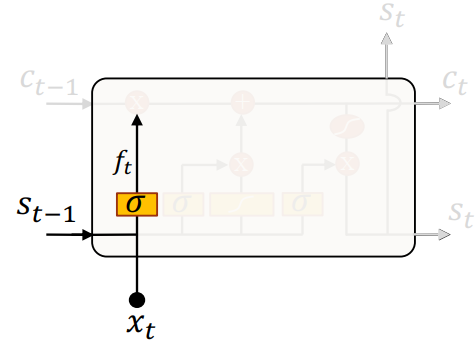
遗忘门接收上一时刻的输出 \(s_{t-1}\) 和这一时刻的输入 \(x_t\)，通过 \(\sigma\) 计算输出 \(f_t\)，然后和向量 \(c_{t-1}\) 的每个维度（状态）逐元素相乘（变为 \(c_{t-1}'\)）。
也就是，根据当前输入，和上一个输出，来判断 \(c_{t-1}\) 中哪些保留的（维度）信息需要被遗忘。
输入门
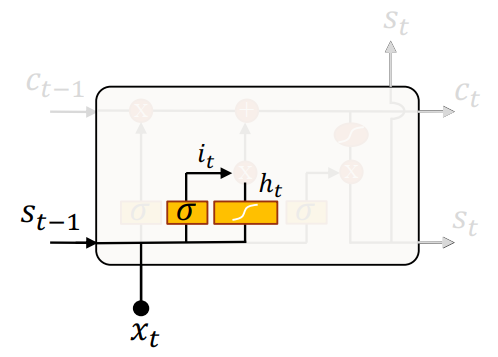
可以看到，输入门接收输入 \(s_{t-1}\) 和 \(x_t\)，之后分为两个部分：
- 用一个 \(\sigma\) 函数的输出 \(i_t\) 判断哪些状态需要更新，并且计算需要更新的权重（对应了Sigmoid的输出，0 到 1）。
- 用一个 \(\tanh\) 函数创建实际要更新的向量 \(h_t\)。
然后将 \(i_t\) 和 \(h_t\) 两个结果相乘，逐元素加到 \(c_{t-1}'\)（变为 \(c_{t-1}''\)）。
也就是，将获取到的新信息加（更新）到传送带 \(c_{t-1}\) 上去。
输出门
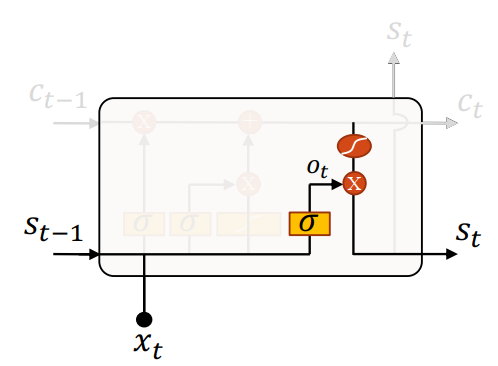
输出门先接收输入 \(s_{t-1}\) 和 \(x_t\)，通过 \(\sigma\) 输出 \(o_t\) 用来判断当前应该输出什么。
然后，结合 \(\tanh\) 平滑化后的 \(c_{t-1}''\)，（逐元素）相乘并作为此时刻的输出。
输出门不修改 \(c_{t-1}\)。
LSTM 解决了梯度消失的问题
可以看到，对于“传送带” \(c_t\)： \[ 新状态 = (旧状态 \times 遗忘比例) + (新输入 \times 输入比例) \] 于是，前面提到的权重相乘导致的梯度消失问题、在这里因为变成了权重相加，解决了。
