深度生成模型

VAE（变分自编码器）

GAN（对抗生成网络）

Flows（流模型）

AR（自回归模型）

Diffusion （扩散模型）

其中与 Transformer 相关的 AR 内容在另外一篇文章讨论。

（基于朱军老师的PPT）

生成模型

判别模型与生成模型

生成式模型、判别式模型、指数族分布、和广义线性模型 - alittlebear’s blog

判别模型参考上文。判别模型的主要技巧包括：SGD 随机梯度下降，BP 反向传播，Dropout 随机暂时抛弃神经元。

对于未知分布 \(D\) 的 i.i.d. 数据 \(\forall i. x_i\sim_{iid} p_D(x)\)，生成模型学习一个模型分布 \(\theta\) 来逼近数据真实分布 \(D\)：

Richard P. Feynmann 曾说过：”What I cannot create, I don’t understand.” 也就是，他认为理解一个事务代表了可以从头去构造、创造这个事务。换句话说，他认为智能的本质是创造和生成，而非判别。而现在生成式大模型的成功也似乎验证了这一想法。

现在各种生成式模型效果都十分不错：

• 用提示词去生成真实感图片、不同风格的图片 - Midjourney-V5, DALLE3（Nano Banana Pro）
• 文字转视频 - Gen-2, Sora, Vidu （Veo 3, Sora 2）
• 文字转3D - ProlificDreamer

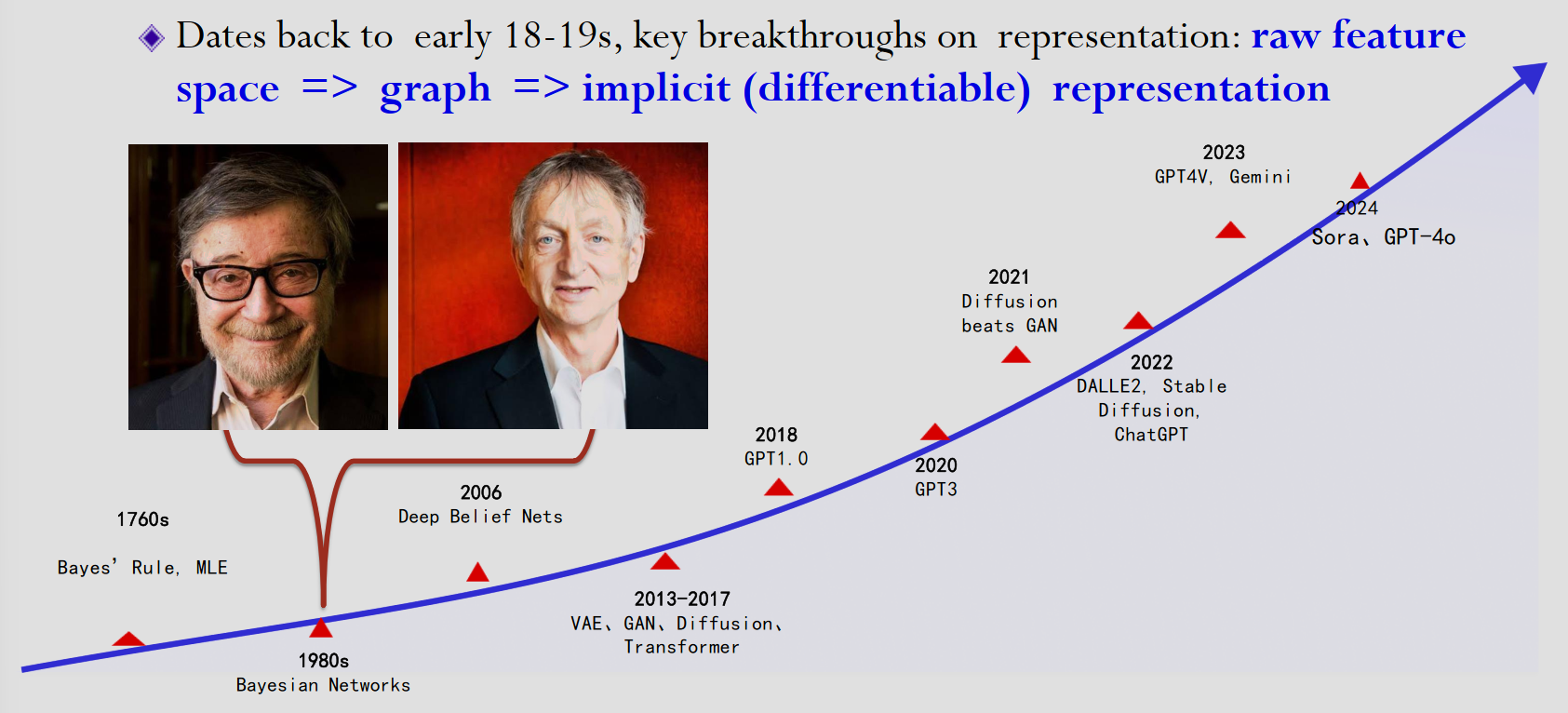
生成模型也经历了三个阶段：从原始数据表示、到图表示、到现在的潜在（可微分）表示。

生成模型的分类

表达方法

现在，生成模型大致可以分为两种：

• 显式模型（Explicit）。如 VAE，基于流（Flow）的模型，以及扩散概率模型（diffusion probabilistic model）。这些模型不仅能生成图片，还能给每一张图片算出一个具体的概率值（或者是概率密度值）\(P(x)\)。
• 隐式模型（Implicit）。如 GAN，匹配矩的生成式网络。这些模型只学会了如何从噪声 \(z\) 映射到数据 \(x\) 的过程（\(x = G(z)\)），无法得知数据出现的概率。

可以看到，显式模型在功能性（异常检测，数据压缩，科学计算）和稳定性都强于隐式模型。隐式模型在 GAN 时期是强于显式模型的，但我们将会看到 Flow 和 Diffusion 这两个显式模型是如何超越 GAN 的。

建模方式

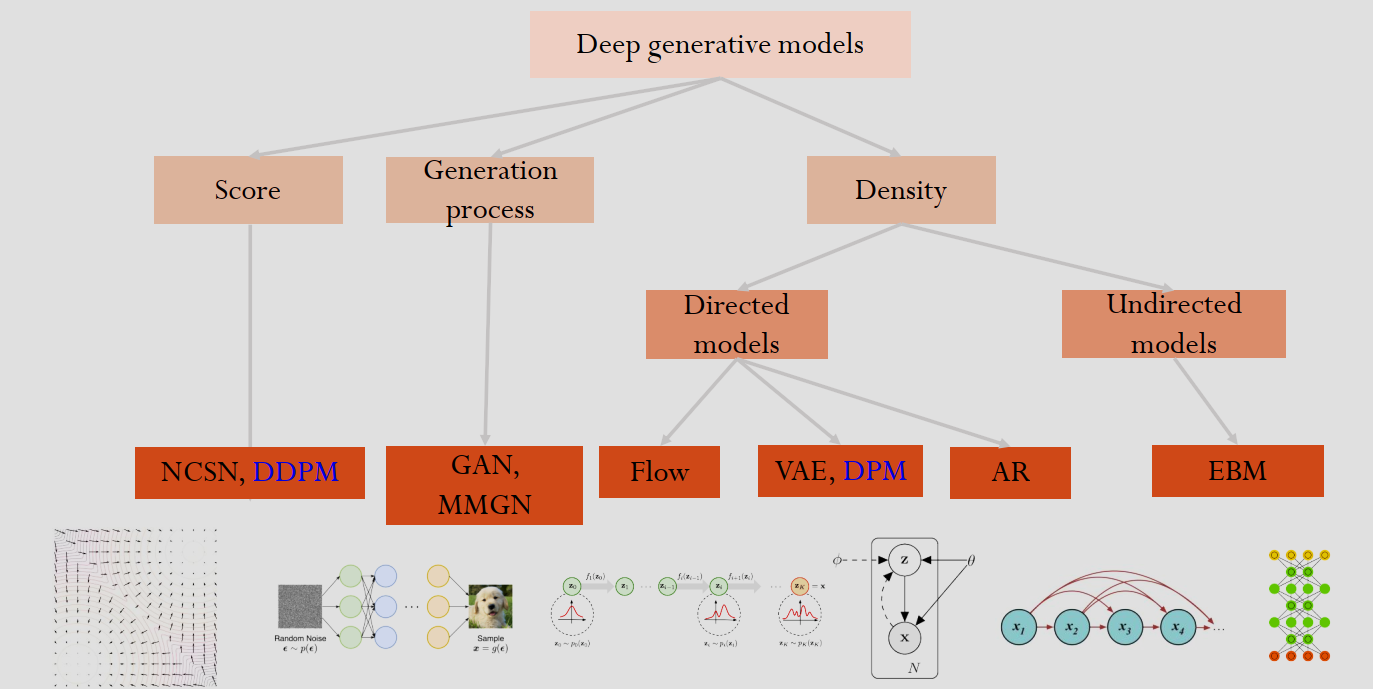
更具体的，可以分为以下建模方式：

1. Score（基于分数的模型）

这一类模型不直接估计概率密度，而是估计概率密度的梯度（即“分数” score）。

• 代表模型：
• NCSN (Noise Conditional Score Network)：噪声条件分数网络。
• DDPM (Denoising Diffusion Probabilistic Models)：去噪扩散概率模型（也就是目前最火的 Diffusion Model 的基础）。注意：图中标蓝的 DDPM 在这里被归类为 Score，因为它的核心训练目标可以看作是分数匹配。
• 底部示意图：
• 左下角的向量场图（Vector Field）。这代表了模型学习的是数据分布的梯度场，箭头指向数据密度更高的方向，指引噪声逐步变成清晰的图像。

2. Generation process（基于生成过程 / 隐式模型）

这一类模型不显式地定义概率分布函数，而是直接学习一个从随机噪声到数据样本的映射机制。

• 代表模型：
• GAN (Generative Adversarial Networks)：生成对抗网络。
• MMGN (Maximum Moment Generative Network)。
• 底部示意图：
• “随机噪声 -> 神经网络 -> 样本”。图中展示了输入随机噪声 \(\epsilon\)，通过生成器 \(g(\epsilon)\)，最终输出一张狗狗的照片。这是 GAN 的典型工作流。

3. Density（基于密度的模型 / 显式模型）

这一类模型试图显式地建模数据的概率分布 \(p(x)\)。根据依赖关系的方向性，又分为两类：

A. Directed models（有向模型）

变量之间的依赖关系是有方向的（通常用贝叶斯网络表示）。

• Flow（流模型）：
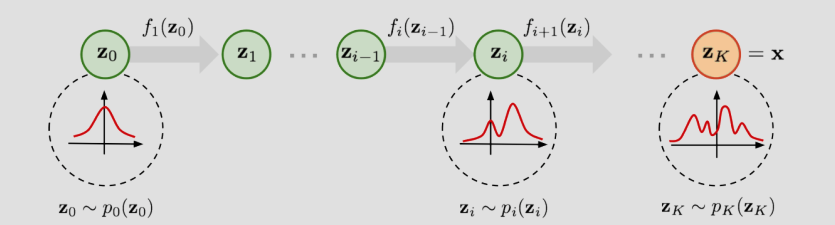
• 概念： 通过一系列可逆的变换（Invertible Transformations），将简单的分布（如高斯分布）映射为复杂的数据分布。
• 示意图： 显示了从 \(z_0\) 到 \(z_k\) 的逐步变换过程，分布形状逐渐改变。
• VAE (Variational Autoencoder) & DPM：
• 概念： 变分自编码器。引入了潜在变量 \(z\)，通过编码器和解码器来最大化数据的证据下界（ELBO）。注意：图里把 DPM 也放在这里，是因为从数学推导上，扩散模型也可以被视为一种层级很深的 VAE。
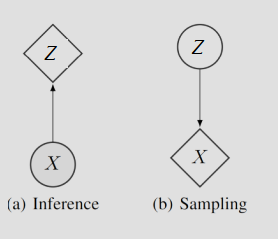
• 示意图： 一个经典的图模型结构，\(\theta\) 是参数，\(z\) 是隐变量，\(x\) 是观测数据，箭头表示生成的方向。
• AR (Autoregressive models)：
• 概念： 自回归模型。将生成任务分解为序列预测，即根据前面的点预测下一个点（例如 GPT 系列就是 AR 模型）。
• 示意图： \(x_1 \to x_2 \to x_3 \dots\) 这种链式结构，表示当前的像素/文字只依赖于之前的像素/文字。

B. Undirected models（无向模型）

变量之间的依赖是双向的，通常基于能量函数（Energy-based）。

• EBM (Energy-Based Models)：
• 概念： 基于能量的模型。它定义一个能量函数，能量越低的状态代表越真实的数据。
• 示意图： 右下角的网格图（类似玻尔兹曼机），节点之间没有箭头方向，表示相互作用是无向的。

学习方法

此外，可以通过学习方法分类：

• MLE：通过最大化（显式的）似然估计 \(\hat{\theta}=\arg\max p(D|\theta)\)

• Minimax 对象（如GAN）：通过两个玩家互相博弈最终达到平衡。

• 矩匹配（Moment-matching）：从 \(p\) 中获取样本： \[ \widehat{D} = \{y_i\}_{i=1}^M, \text{ where } y_i \sim p(x|\theta) \] 然后通过核最大均值差异（Kernel MMD）来优化： \[ \mathcal{L}_{MMD^2} = \left\| \frac{1}{N} \sum_{i=1}^{N} \phi(x_i) - \frac{1}{M} \sum_{j=1}^{M} \phi(y_i) \right\|_{\mathcal{H}}^2 \] 想法和MLE类似，不过MLE是直接用原始分布来对目前分布进行优化，而Kernel MMD是通过矩来进行拟合。

现在主流的生成模型

深度学习中的生成模型可以被划分为四大主要范式：自回归模型 (AR)、变分自编码器 (VAE)、流模型 (Flow) 和 扩散模型 (Diffusion)。

1. 四大生成范式的要点概括

这些模型的核心区别在于如何建模数据分布 \(P(x)\)：

• AR (Autoregressive): 将 \(P(x)\) 拆解为条件概率的乘积 \(P(x) = \prod P(x_i | x_{<i})\)。通过预测“下一个”元素来建模，具有极强的逻辑连贯性，但采样速度慢。
• VAE (Variational Autoencoder): 通过引入隐变量 \(z\) 并引入瓶颈（Bottleneck）结构，通过最大化证据下界 (ELBO) 来近似 \(P(x)\)。采样快但图像容易模糊。
• Flow (Normalizing Flow): 使用一系列可逆变换将简单分布（如高斯分布）映射到复杂数据分布。它能计算精确的似然值，但模型结构受限于“可逆性”。
• Diffusion: 通过逐渐加噪（正向）和去噪（反向）的过程来生成数据。它在数学上可以看作是带有多个隐层的 VAE，目前在生成质量上处于 SOTA。

关联

2. 何恺明的 MAE 是 AR 和 VAE 的融合吗？

结论：MAE (Masked Autoencoder) 本质上是“去噪自编码器 (DAE)”在视觉领域的极致简化，它借鉴了 AR 的学习范式，但并非 VAE。

• 与 AR 的关系（借鉴范式）：

  MAE 的核心思想是 Masked Image Modeling (MIM)。这直接受到 NLP 中 BERT（Masked LM）的启发。

  • 虽然 MAE 不是像 GPT 那样逐个像素预测的自回归，但它采用的“掩码再重建”逻辑与 AR 的“根据已知预测未知”在哲学上是一致的。

• 与 VAE 的关系（架构相似，本质不同）：

  • 架构上： MAE 确实有 Encoder 和 Decoder，看起来像 VAE。
  • 本质上： MAE 是确定性的自编码器。它没有 VAE 那样的隐变量分布假设（即没有 \(z \sim N(0, I)\) 的约束，也没有 KL 散度项）。它只负责把缺失的像素“填回来”，而不负责学习一个连续的生成空间。因此，MAE 更多被视为自监督预训练工具，而非纯粹的生成模型。

[!NOTE]

MAE 抛弃了 VAE 的概率论约束，转而追求在极高掩码率（如 75%）下的表征学习能力。

---

3. Flow 和 Diffusion 有融合吗？

结论：有，且这是当前生成模型领域最前沿的研究方向之一，最典型的融合产物是“流匹配 (Flow Matching)”。

实际上，扩散模型和流模型在数学上有着深刻的内在联系：

1. 概率流 ODE (Probability Flow ODE)

扩散模型（如 DDPM）在反向去噪时可以被转换成一个确定性的常微分方程（ODE）。这个 ODE 的轨迹本质上就是一个连续时间流模型 (Continuous Normalizing Flow)。

2. 流匹配 (Flow Matching, FM)

这是目前最火的融合范式。

• 逻辑： 传统的扩散模型路径是弯曲且充满噪声的。流匹配通过引入流的思想，试图学习一个线性（直的）的变换轨迹。
• 优势： 由于轨迹是直的，推理时步长可以迈得更大，从而解决了扩散模型采样慢的问题，同时保留了扩散模型处理高维数据的稳定性。
• 代表作： Stable Diffusion 3 (SD3) 就采用了 Rectified Flow 技术，这正是 Flow 与 Diffusion 的深度融合。

---

4. 四大模型关系总结表

特性	AR (如 GPT)	VAE	Flow	Diffusion
目标	似然函数 \(P(x)\)	ELBO (证据下界)	精确似然 (可逆变换)	分数匹配 (Score Matching)
核心优势	逻辑极强，离散数据王者	采样极快，隐空间易插值	数学优美，显式概率	生成质量最高，训练稳定
主要劣势	采样速度 O(N)	图像模糊	架构受限 (必须可逆)	采样需要多次迭代
与 MAE 关系	MAE 是其非因果版本	架构类似，但 MAE 没概率项	无直接关系	无直接关系

变分自编码器 Variational Auto-Encoder （VAE）

变分贝叶斯 Variational Bayes

对于隐变量 \(z\)，考虑一个数据点的log似然的公式： \[ \log p(\mathrm{x}; \theta) = \log \int p(\mathrm{z}, \mathrm{x}; \theta) d\mathrm{z} \] 但对数里面套积分非常难处理，尤其是高维空间，为此，考虑辅助分布 \(q(z|x; \phi)\) 来近似真实的后验分布，可以写成： \[ \begin{aligned} \log p(\mathrm{x}; \theta) &= L(\theta, \phi, \mathrm{x}) + \mathrm{KL}(q(\mathrm{z}|\mathrm{x}; \phi) \| p(\mathrm{z}|\mathrm{x}; \theta)) \\ L(\theta, \phi, \mathrm{x}) &= \mathbf{E}_{q(\mathrm{z}|\mathrm{x}; \phi)} [\log p(\mathrm{z}, \mathrm{x}; \theta) - \log q(\mathrm{z}|\mathrm{x}; \phi)] \\ &= \mathbf{E}_{q(\mathrm{z}|\mathrm{x}; \phi)} [\log p(\mathrm{x}|\mathrm{z}; \theta) + \log p(\mathrm{z}; \theta) - \log q(\mathrm{z}|\mathrm{x}; \phi)] \\ &= \underbrace{\mathbf{E}_{q(\mathrm{z}|\mathrm{x}; \phi)} [\log p(\mathrm{x}|\mathrm{z}; \theta)]}_{\text{reconstruction term}} - \underbrace{\mathrm{KL}(q(\mathrm{z}|\mathrm{x}; \phi) \| p(\mathrm{z}; \theta))}_{\text{prior regularization}} \end{aligned} \] 其中 \(L\) 被称为 ELBO （Evidence Lower Bound，证据下界）。Reconstruction term （重构项）可以看作是从近似分布 \(q\) 中采样出一个 \(z\)（编码），通过生成网络 \(p\)（解码）还原回 \(x\) 的概率；Prior Regularization（先验正则化）在限制近似分布 \(q(z|x)\)（编码器的输出分布），让它不要偏离先验分布 \(p(z)\)（通常假设为标准正态分布 \(\mathcal{N}(0, I)\)）太远。

于是，由于 KL 散度不小于0，最大化对数似然可以通过最大化 \(L\) 来间接获得。

自编码器 Auto-Encoder（AE）

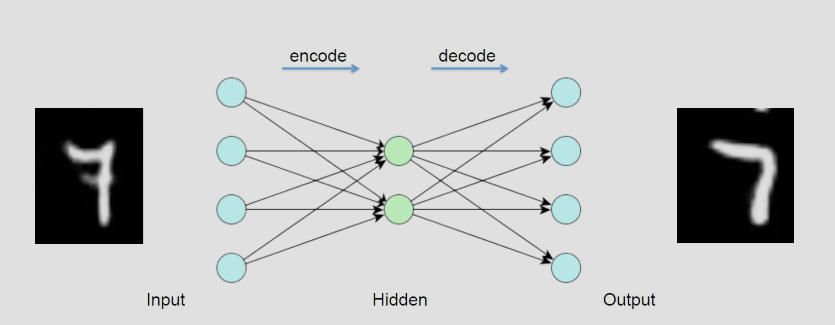
自编码器可以看作两个部分：编码器（Encoder）和解码器（Decoder）。目标就是最小化重构错误。

去噪自编码器（Denoising AE）通过给输入添加随机噪点来增加模型重构的鲁棒性。

变分（贝叶斯）自编码器 Auto-Encoding Variational Bayes（AEVB）

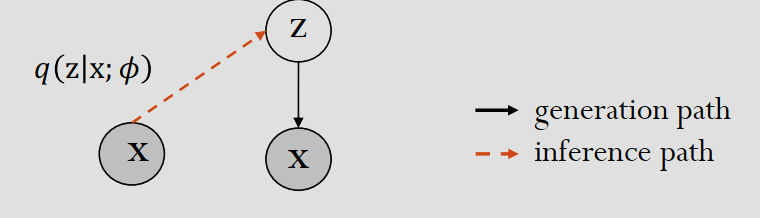
与其像 AE 一样重构一个具体的输出，不如扩展为输出一个概率分布（\(\mu, \sigma^2\)），然后从分布随机采样一个点作为输出，这样可以对于难以重构的目标进行“生成”。这也被称为推理网络 inference network（或者Q-network）

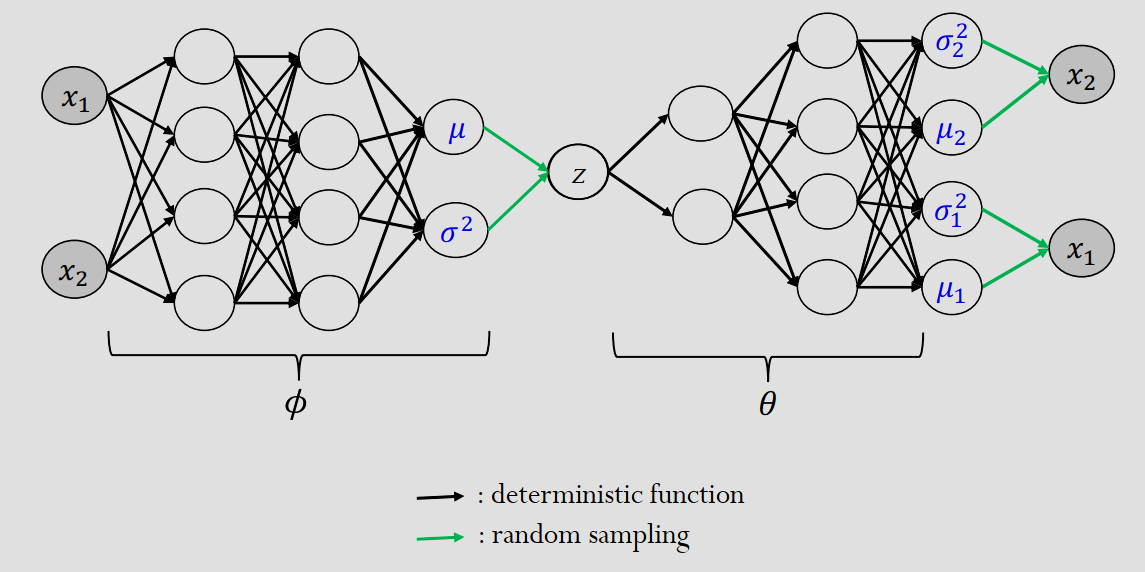
正如前面所说，AEVB 优化 ELBO \(L\)。前面给出的一个数据的 \(L\) 是： \[ L(\theta, \phi, \mathrm{x}) = \underbrace{\mathbf{E}_{q(\mathrm{z}|\mathrm{x}; \phi)} [\log p(\mathrm{x}|\mathrm{z}; \theta)]}_{\text{reconstruction term}} - \underbrace{\mathrm{KL}(q(\mathrm{z}|\mathrm{x}; \phi) \| p(\mathrm{z}; \theta))}_{\text{prior regularization}} \] 扩展为一组数据： \[ L(\theta, \phi, D) = \sum_{i}\underbrace{\mathbf{E}_{q(\mathrm{z_i}|\mathrm{x_i}; \phi)} [\log p(\mathrm{x_i}|\mathrm{z_i}; \theta)]}_{\text{reconstruction term}} - \underbrace{\mathrm{KL}(q(\mathrm{z_i}|\mathrm{x_i}; \phi) \| p(\mathrm{z_i}; \theta))}_{\text{prior regularization}} \] 其中 \(z\) 的先验分布为 \(\cal{N}(0,1)\)，\(q(z|x;\phi)\) 是根据神经网络决定的 \(\cal{N}(\mu(x;\phi),\sigma^2(x;\phi))\)，KL散度是\(-\mathrm{KL}(q(z|x; \phi) \| p(z; \theta)) = \frac{1}{2} (1 + \log \sigma^2 - \mu^2 - \sigma^2)\)。

对于重建项 \(\mathbf{E}_{q(\mathrm{z}|\mathrm{x}; \phi)} [\log p(\mathrm{x}|\mathrm{z}; \theta)]\)，假设数据似然为高斯分布，那么随机变量是 \(-\log p(\mathrm{x}_i|\mathrm{z}_i) = \sum_{j} \frac{1}{2} \log \sigma_j^2 + \frac{(x_{ij} - \mu_{xi})^2}{2\sigma_j^2}\)，可以看到由于是非线性函数，其期望值特别难计算。

于是，我们用蒙特卡洛法来模拟近似期望值 \[ \begin{gathered} \mathbf{E}_{q(z|x;\phi)}[\log p(x|z; \theta)] \approx \frac{1}{L} \sum_{k} \log p(x|z^{(k)}) \\ z^{(k)} \sim q(z|x; \phi) \end{gathered} \] KL散度可以看到梯度计算是没问题的，但重建项由于设计了网络中 \(z\) 的随机采样这个随机离散操作，不可导。

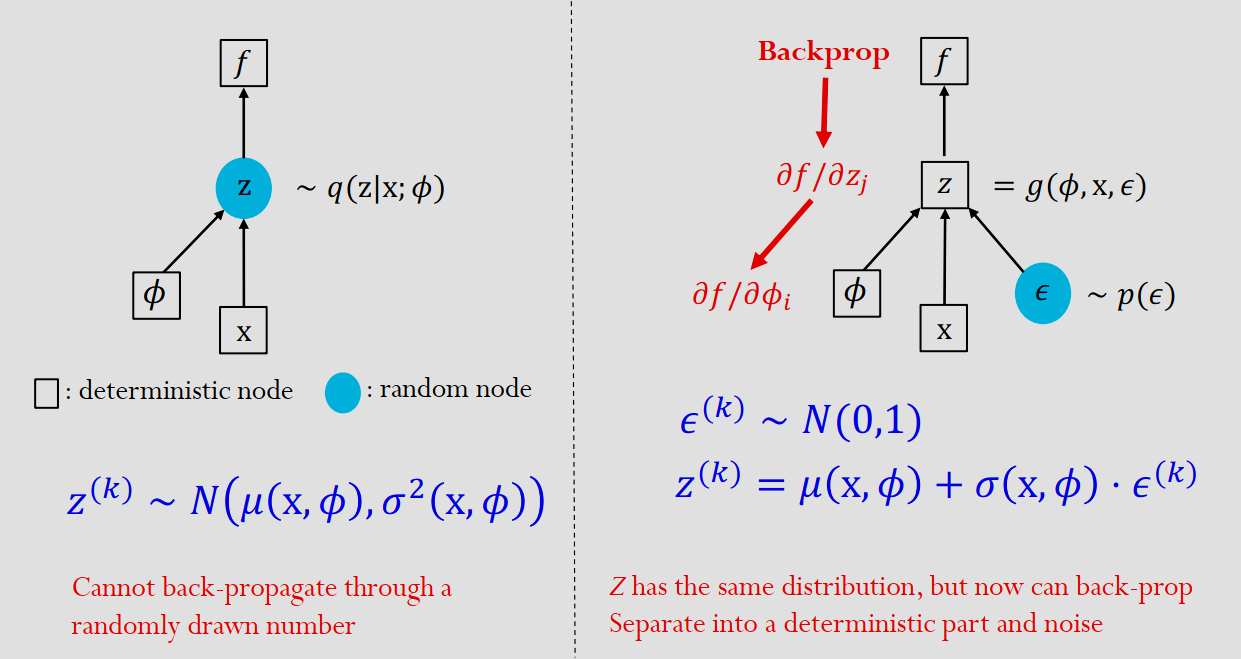
为了解决这个问题，与其直接从带参数的分布中采样 \(z\)，不如将 \(z\) 的随机性转移到 \(\epsilon\) 去，然后用随机的 \(\epsilon\) 来合成 \(z\)，并且还不影响网络其他地方的确定性（BP算法需要确定性）。

于是， 通过这个重参数化技巧，我们就让原始的 \(L\) 从 \[ L(\theta, \phi, \mathbf{x}) = \mathbf{E}_{q(\mathbf{z}|\mathbf{x};\phi)} \left[ \log \frac{p(\mathbf{z}, \mathbf{x}; \theta)}{q(\mathbf{z}|\mathbf{x}; \phi)} \right] \] 变为 \[ L(\theta, \phi, \mathbf{x}) = \mathbf{E}_{p(\epsilon)} \left[ \log \frac{p(g(\mathbf{x}, \epsilon, \phi), \mathbf{x}; \theta)}{q(g(\mathbf{x}, \epsilon, \phi)|\mathbf{x}; \phi)} \right] \] 其中 \(g\) 是一个神经网络，\(\epsilon\) 是 \(\cal{N}(0,1)\)。

并得到最终（可以通过BP更新的）梯度： \[ \nabla_\theta L(\theta, \phi, \mathbf{x}) = \mathbf{E}_{p(\epsilon)} \left[ \nabla_\theta \log \frac{p(g(\mathbf{x}, \epsilon, \phi), \mathbf{x}; \theta)}{q(g(\mathbf{x}, \epsilon, \phi)|\mathbf{x}; \phi)} \right] \]

重要性加权自编码器 Importance Weighted Auto-Encoder（IWAE）

考虑原始 ELBO： \[ L(\theta, \phi, \mathbf{x}) = \mathbf{E}_{q(\mathbf{z}|\mathbf{x};\phi)} \left[ \log \frac{p(\mathbf{z}, \mathbf{x}; \theta)}{q(\mathbf{z}|\mathbf{x}; \phi)} \right] \] 最大化ELBO，因KL项的存在，不一定最大化log似然。但我们可以通过优化一个更好的下界，来给一个更紧的log似然下界： \[ L_K(\theta, \phi, \mathbf{x}) = \mathbf{E}_{q(\mathbf{z}|\mathbf{x};\phi)} \left[ \log \left( \frac{1}{K} \sum_{k=1:K} \frac{p(\mathbf{z}^{(k)}, \mathbf{x}; \theta)}{q(\mathbf{z}^{(k)}|\mathbf{x}; \phi)} \right) \right] \] 这里 \(\mathbf{z}^{(k)} \sim q(\mathbf{z}|\mathbf{x}; \phi)\)，当 \(K=1\) 时就退化成了前面的 ELBO，随着 \(K\) 增大，下界单调递增，趋于真实的log似然 \(\log p(x)\)。

当然，为了 BP 能够运行，IWAE： \[ L_K(\theta, \phi, \mathbf{x}) = \mathbf{E}_{q(z|\mathbf{x};\phi)} \left[ \log \left( \frac{1}{K} \sum_{k=1:K} w(z^{(k)}, \mathbf{x}; \theta) \right) \right] \]

\[ \text{where } z^{(k)} \sim q(z|\mathbf{x}; \phi) \]

\[ w(z^{(k)}, \mathbf{x}; \theta, \phi) = \frac{p(z^{(k)}, \mathbf{x}; \theta)}{q(z^{(k)}|\mathbf{x}; \phi)} \]

也要重参数化： \[ L_K(\theta, \phi, \mathbf{x}) = \mathbf{E}_{p(\boldsymbol{\epsilon})} \left[ \log \left( \frac{1}{K} \sum_{k=1:K} w(g(\epsilon^{(k)}, \mathbf{x}, \phi), \mathbf{x}; \theta) \right) \right] \]

\[ \text{where } \epsilon^{(k)} \sim p(\epsilon) \]

网络架构

这里是 MLP 的 Q-P 变分自编码器 VAE 的架构：

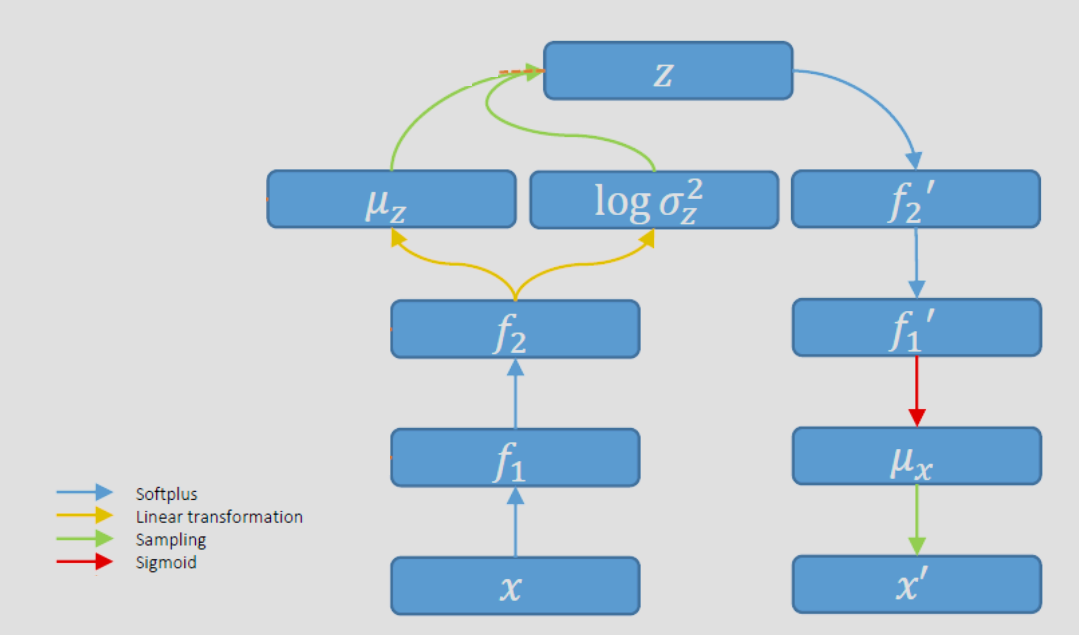
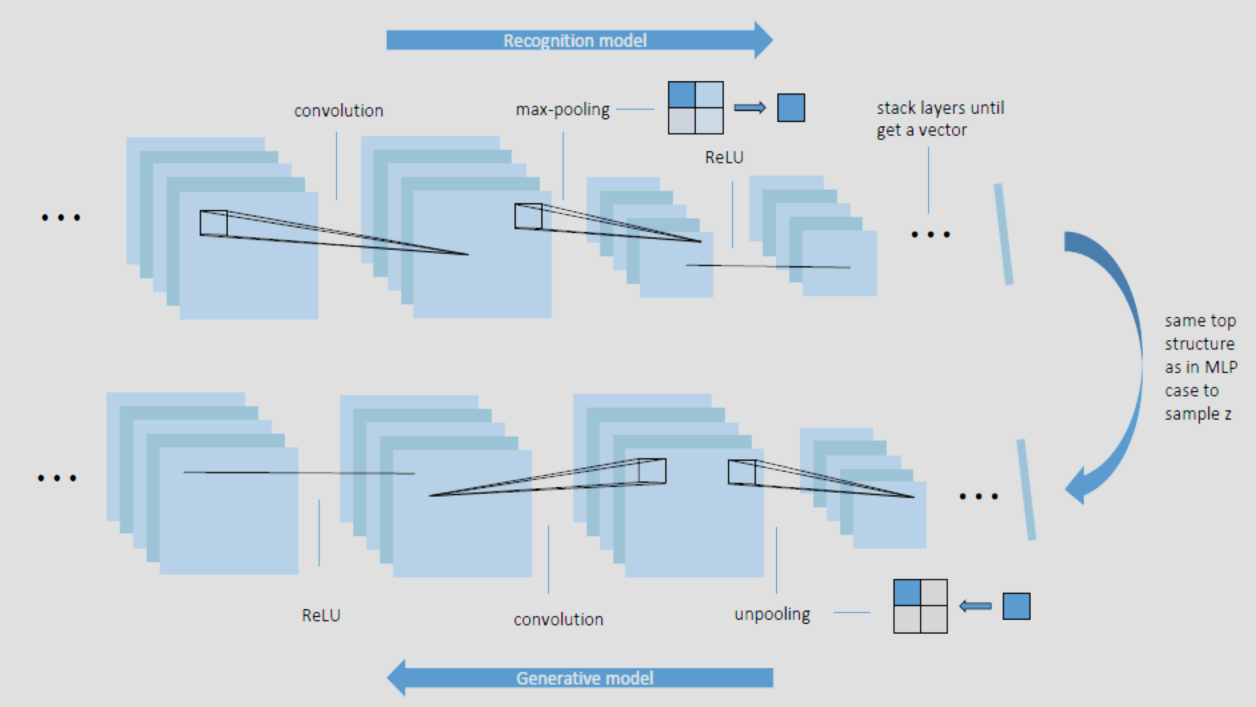
VAE 除了可以用普通 MLP 神经网络实现，还可以通过 CNN 实现：

生成对抗网络 Generative Adversarial Networks （GAN）

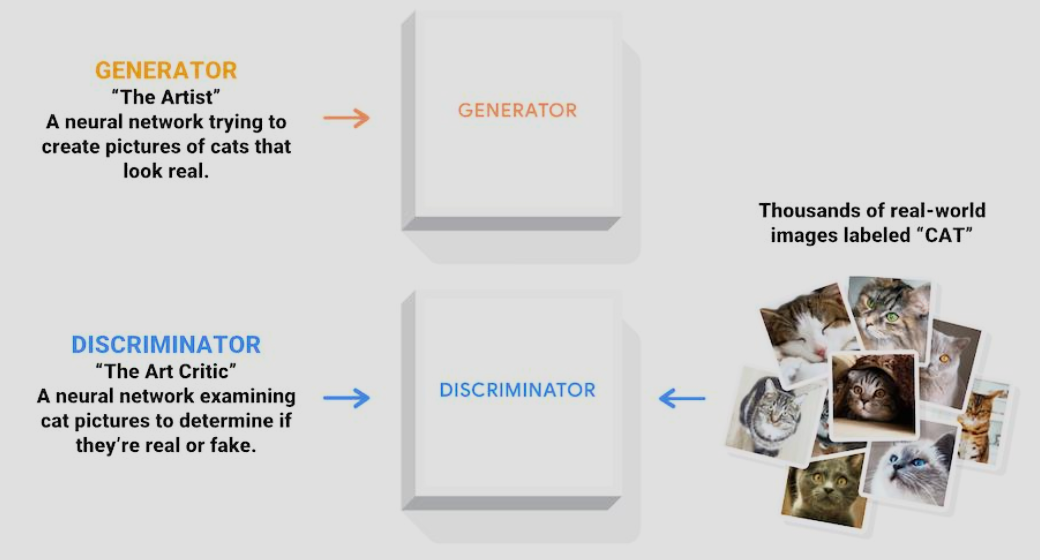
生成式对抗网络可以看作是两个玩家互相博弈，一个玩家（Generator）负责生成图像，一个玩家（Discriminator）负责判别、分辨图像是否是由对方（Generator）生成的，还是真实数据样本。可以看到，当玩家 D 无法区分玩家 G 生成的图像时，可以说生成出来的输出基本是符合原始输入流行的。

更具体的，生成网络 G 从噪音中生成样本：

判别网络 D 作为一个二元分类器，尝试对真实和生成出来的样本进行分类（有监督学习）：

优化

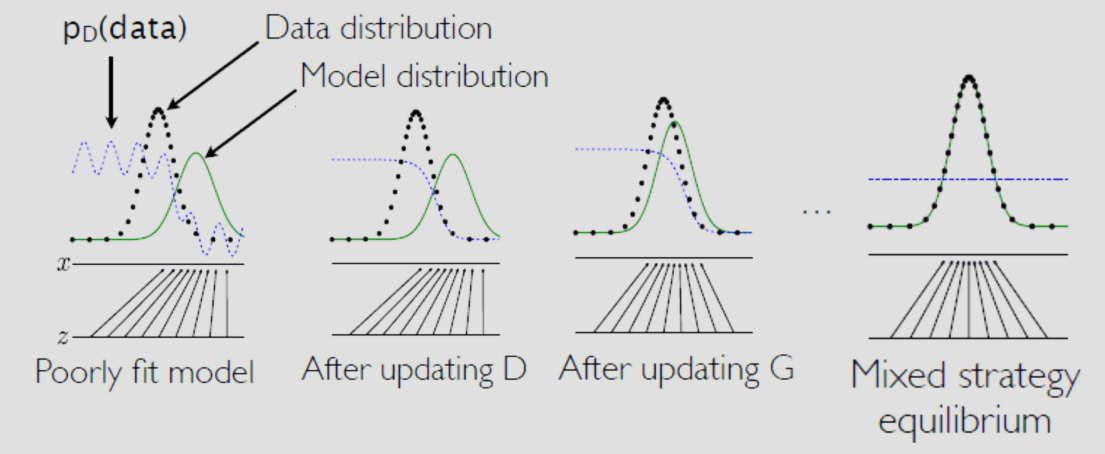
由于对抗式的机制，需要一方更新后才能让另一方更新，这样循环直到收敛。

形式上来说，D 的优化目标天然的就对应了 MLE： \[ \max_D \mathbf{E}_{p_{\text{data}}(x)}[\log D(x)] + \mathbf{E}_{p(z)} \left[ \log \left( 1 - D(G(z)) \right) \right] \] 其中 \(p_{\text{data}}\) 来自训练集， \(p(z)\) 来自生成器 \(G(z)\)，\(D(x)=p(y=1|x)\)。这也叫 Cross-entropy loss minimization。可以看到，我们想要同时优化模型 D 将真实样本和 G 生成的数据正确识别出。

G 的优化目标为最大化生成数据被 D 判别为真实数据的期望值： \[ \max_G \mathbf{E}_{p(z)} \left[ \log \left( D(G(z)) \right) \right] \] 等价的： \[ \min_G \mathbf{E}_{p(z)} \left[ \log \left( 1 - D(G(z)) \right) \right] \] 于是，GAN 的 minimax 策略就是： \[ \min_G \max_D \mathbf{E}_{p_{\text{data}}(x)}[\log D(x)] + \mathbf{E}_{p(z)} \left[ \log \left( 1 - D(G(z)) \right) \right] \] 对于给定生成器 \(G\)，判别器 D 有解析最优解（通过对上述函数进行偏导得出）： \[ D(x) = \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_{\text{model}}(x)} \] 可以看到，假设数据无限，模型容量无限，生成器 G 存在全局唯一最优 - 也就是数据分布。

对于 G，假设 D 已为最优，带入到 minimax 价值函数： \[ \mathbb{E}_{x \sim p_{\text{data}}} \left[ \log \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_g(x)} \right] + \mathbb{E}_{x \sim p_g} \left[ \log \frac{p_g(x)}{p_{\text{data}}(x) + p_g(x)} \right] \] 根据定义： \[ KL(\mathbb{P}_r \| \mathbb{P}_g) = \int \log \left( \frac{P_r(x)}{P_g(x)} \right) P_r(x) d\mu(x) \]

\[ JS(\mathbb{P}_r, \mathbb{P}_g) = KL(\mathbb{P}_r \| \mathbb{P}_m) + KL(\mathbb{P}_g \| \mathbb{P}_m) \]

\[ \mathbb{P}_m = (\mathbb{P}_r + \mathbb{P}_g)/2 \]

\[ W(\mathbb{P}_r, \mathbb{P}_g) = \inf_{\gamma \in \Pi(\mathbb{P}_r, \mathbb{P}_g)} \mathbb{E}_{(x, y) \sim \gamma} \left[ \| x - y \| \right] \]

变形为： \[ -\log 4 + KL \left( p_{\text{data}} \parallel \frac{p_{\text{data}} + p_g}{2} \right) + KL \left( p_g \parallel \frac{p_{\text{data}} + p_g}{2} \right) \]

\[ -\log 4 + 2 \cdot JS(p_{\text{data}} \parallel p_g) \]

也就是，最小化 G 等价于最小化 Jenson-Shannon 散度。

JS 距离的问题

可以看到，上面推导出了生产器 G 在判别器 D 为最优时，实际上就是在最小化生成分布与真实分布之间的 JS 散度。

但，考虑这个例子：

• 假设真实分布 \(P_0\) 是二维平面上 \((0, Z)\) 线段上的均匀分布（\(Z \sim U[0,1]\)）。

• 假设生成分布 \(P_\theta\) 是平行线段 \((\theta, Z)\) 上的均匀分布。

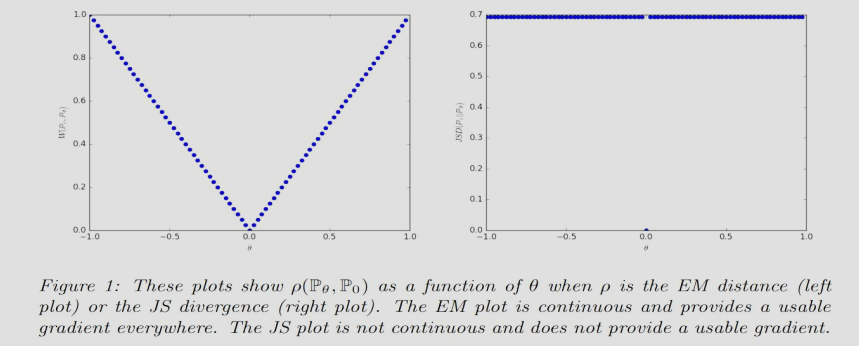
那么我们有 Kullback-Leibler （KL） 散度： \[ KL(\mathbb{P}_\theta \| \mathbb{P}_0) = KL(\mathbb{P}_0 \| \mathbb{P}_\theta) = \begin{cases} +\infty & \text{if } \theta \neq 0 \\ 0 & \text{if } \theta = 0 \end{cases} \] Jensen-Shannon（JS） 散度： \[ JS(\mathbb{P}_0, \mathbb{P}_\theta) = \begin{cases} \log 2 & \text{if } \theta \neq 0 , \\ 0 & \text{if } \theta = 0 , \end{cases} \] Wasserstein-1（W，或者 Earth-Mover EM）散度： \[ W(\mathbb{P}_0, \mathbb{P}_\theta) = |\theta|, \] 可以看到 KL 值为正无穷或0，梯度无定义或为0（无意义）；类似的，JS 梯度为0（当 \(\theta\ne0\)）或无定义（\(\theta=0\)）；但，在这个情况 \(W\) 的值为 \(|\theta|\)（连续函数），处处存在有意义梯度（导数在 \(\{-1,1\}\)），这意味着在这种极端情况 JS 无法进行优化的时候，W 散度还是可以优化生成器。

解决方法

在下面 WGAN 问世前，有以下方法用来缓解上述问题：

• 在 GAN 中，如果 D 完美的区分了真实样本和生成出来的，那么这就导致 G 的梯度消失，无法训练。为了解决这个问题，可以减缓 D 的训练性能。
• 训练初期直接优化 \(\min_G \mathbb{E}[\log(1 - D(G(z)))]\) 时当 G 性能很低，梯度无法更新。为此，可以将目标变为 \(\max_G \mathbb{E}[\log(D(G(z)))]\) 来让梯度早期更新更快。

Wasserstein GAN（WGAN）

WGAN 从根本上解决了上述问题。WGAN 的目标函数为： \[ \min_{G}\max_{D} \mathbb{E}_{x \sim P_{data}}[D(x)] - \mathbb{E}_{z \sim P(z)}[D(G(z))] \] 为了让其几乎处处可导，判别器 D 从二元分类器限制为 1-Lipschitz 函数（可以通过权重剪裁 Weight Clipping，即在每次更新后强制将 Critic 的参数限制在一个小范围内如 \([-0.01, 0.01]\) 来限制 D 为 1-Lipschitz 函数）。

然后，目标函数就从优化 JS 变为了优化 W 距离。

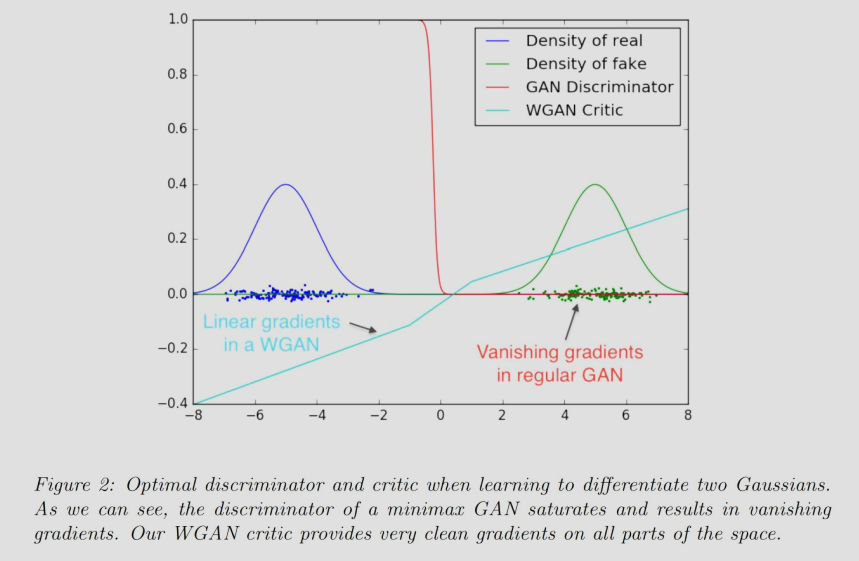
可以看到，在（G 性能很差，D 性能很好的）极端情况下，GAN 的梯度为 0 无法更新；但 WGAN 始终保持线性梯度。

从控制论的角度看 GAN

当生成器想靠近真实分布，而判别器想把它们推开时，双方的参数更新轨迹往往不是直接收敛到中心，而是形成一个极限环 (Limit Cycle)，一直在绕圈圈。

为了数学化地描述这种“绕圈圈”的现象，引入动力系统的稳定性分析：

将训练看作动力系统：参数 \(\theta\) 随时间的变化率由梯度向量场 \(v(\theta)\) 决定。

雅可比矩阵 (Jacobian Matrix)：要看一个均衡点稳不稳定，就要看这个点附近的雅可比矩阵的特征值 (Eigenvalues)。

• 如果特征值的实部 \(>0\)：系统发散（参数飞了）。
• 如果特征值的实部 \(=0\)（纯虚数）：系统震荡（绕圈圈，既不收敛也不发散）。

结论：标准 GAN 在纳什均衡点附近的特征值往往主要集中在虚轴上（纯虚数），这意味着SimGD 本质上就是不稳定的，它天然倾向于震荡而不是收敛。

闭环控制 GAN Closed-loop control（CLC-GAN）

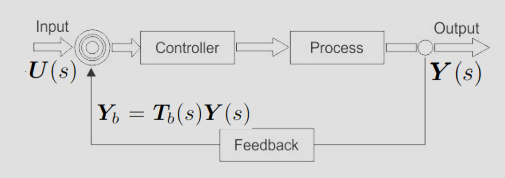
CLC-GAN 对以上问题的解决思路就是，在原有的梯度向量场 \(v(\theta)\) 上，加一项控制项 (Control Term)，这样保证了模型会收敛到纳什均衡点。

通过李雅普诺夫分析（Lyapunov analysis），可以从数学上证明以上修改后的动力系统是渐进稳定的。

可以看到，WGAN 和 Hinge-GAN 的传递函数是纯震荡的，而 SGAN 和 LSGAN 是不稳定的。在添加了控制项变为 CLC-GAN 后，所有主流 GAN 架构都变得（理论和实践上）稳定了。

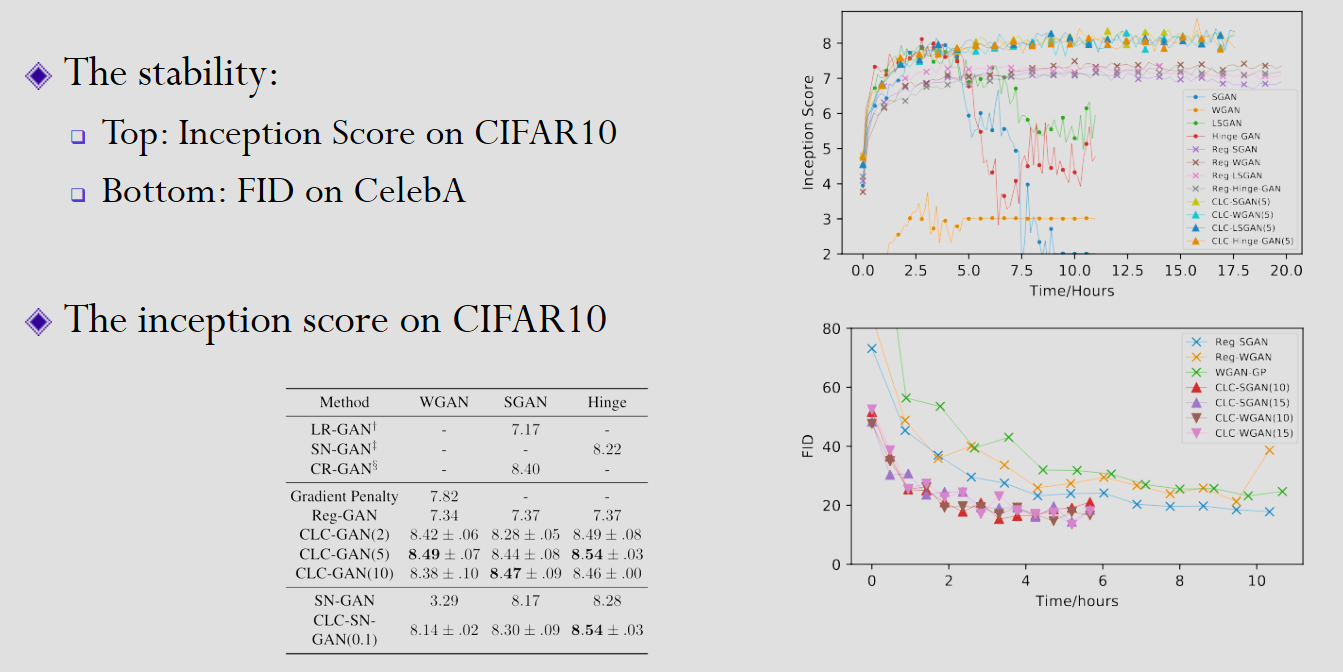
可以看到，添加了 CLC 架构的 GAN，FID score（生成与真实分布的距离）收敛速度显著提升，并且 Inception score（清晰度和多样性的指标）

流模型 Flow-based Model

Flow

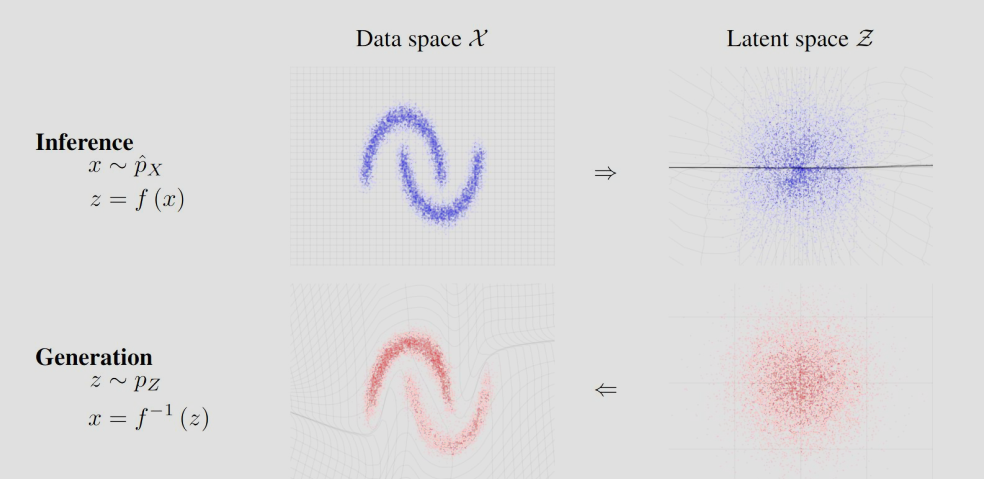
VAE 虽然是显式模型，但优化只能通过下界 ELBO。GAN 效果虽然不错，但是隐式模型，无法计算似然。

为此，引入显式流模型（Flow-based Model），我们希望整个过程可导可逆，所以所有函数都是双射（可逆）。

现在考虑具体函数。假设 \(z=f(x)\) 并且 \(f\) 可逆，那么密度函数为： \[ p(z)=p(f(x))\left|\det\frac{\partial f(x)}{\partial x}\right| \] 可以看到核心难点在于计算 Jacobian 矩阵。

于是，为了简化 Jacobian 矩阵，最简单的想法就是使用耦合层 (Coupling Layers)，即把 \(x\) 切成两半（从向量维度上分成两部分），一半不变，另一半做变换。虽然好算，但表达能力受限。更具体的，将 \(x\) 分为 \(x_1,x_2\) 并定义 \(y_1=x_1, y_2=x_2+m(x_1)\)，其中 \(m\) 可以是任意函数，如 ReLU。

通过这种方法得到的 \(f\)（显然是双射并存在逆），可以看到 Jacobian 的 determinant 就是 1： \[ J = \frac{\partial y}{\partial x} = \begin{bmatrix} \frac{\partial y_1}{\partial x_1} & \frac{\partial y_1}{\partial x_2} \\ \frac{\partial y_2}{\partial x_1} & \frac{\partial y_2}{\partial x_2} \end{bmatrix} = \begin{bmatrix} I & 0 \\ \frac{\partial m}{\partial x_1} & I \end{bmatrix} \]

基于此想法，定义最终函数为上述 \(f\) 的组合，可以看到这个组合也是可逆，且 Jacobian 的 determinant 易计算。这个序列就叫做流（Flow）

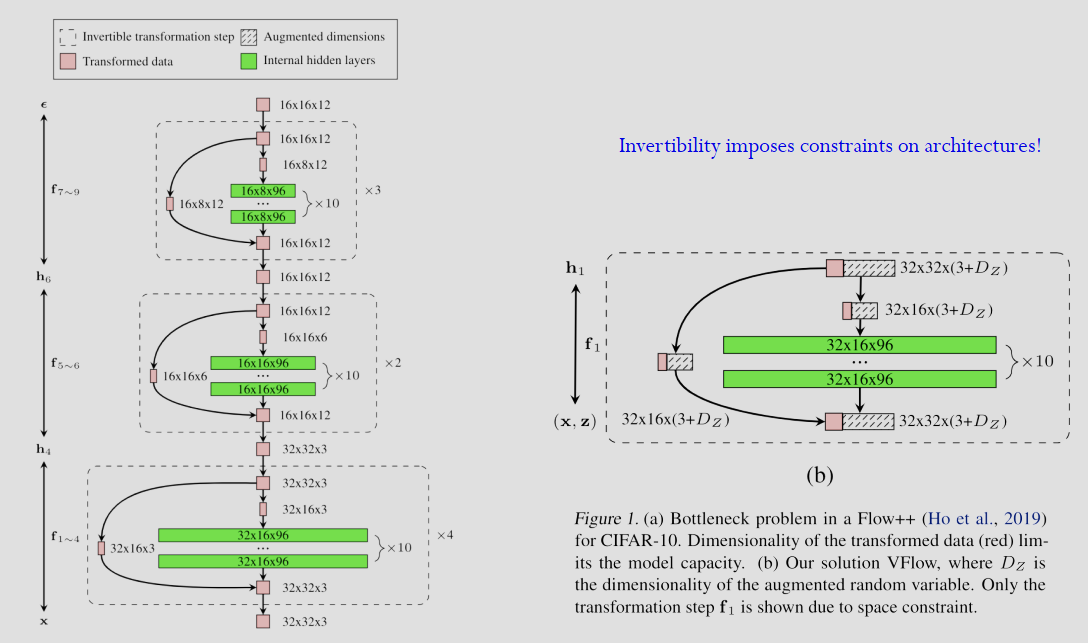
维度瓶颈与 VFlow

Flow 模型要求隐变量 \(z\) 维度与输入 \(x\) 完全一致。但，数据实际流行的维度可能远小于数据维度，这种强行双射导致了隐变量会强制为了填满所有维度对数据进行扭曲，学习困难。

为了解决这个问题，Variational Flow （VFlow） 不直接建模 \(p(x)\)，而是引入辅助变量 \(v\) 将输入 \(x\) 扩展为 \((x,v)\)，然后对这个扩展后的空间进行可逆映射关系：\(z=f(x,v)\)。

由于 \(v\) 未知，和 VAE 一样，只能优化变分下界 ELBO \[ u \sim \mathcal{N}(0, I) \]

\[ y = concat([x, z]) \]

\[ \log p(x, z) = \log p(u) + \log \det(\frac{du}{dy}) \]

\[ \log p(x) \geq \mathrm{E}_{q(z|x)} [\log p(x, z) - \log q(z|x)] \]

\[ \max_{\boldsymbol{\theta}, \boldsymbol{\phi}} \mathbb{E}_{\hat{p}(\mathbf{x}) q(\mathbf{z}|\mathbf{x};\phi)} [\log p(\mathbf{x}, \mathbf{z}; \boldsymbol{\theta}) - \log q(\mathbf{z}|\mathbf{x}; \boldsymbol{\phi})] \]

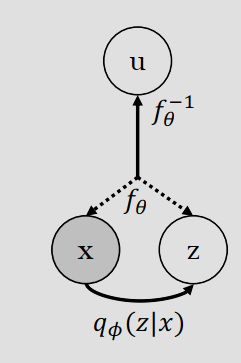
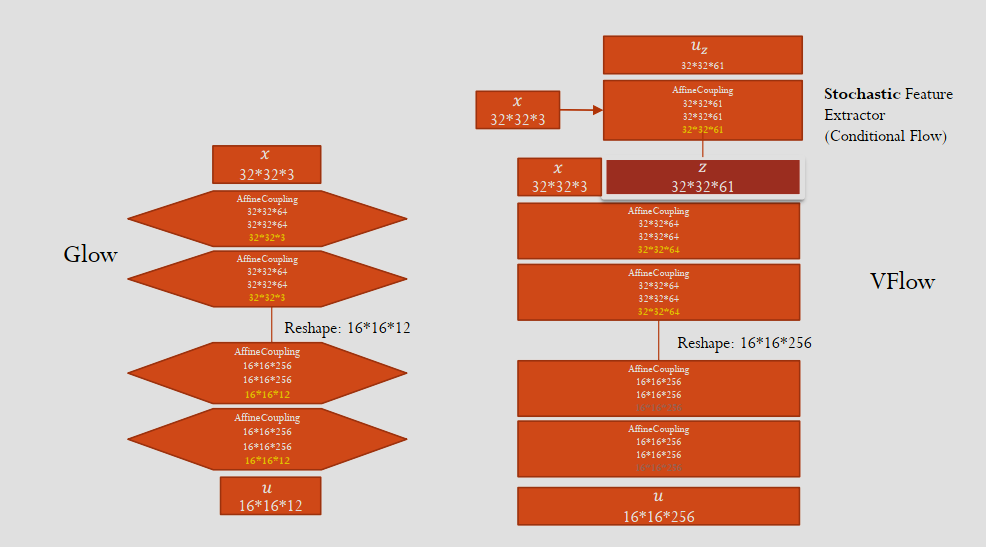
可以看到，当 \(v\) 的维度为 0，VFlow 退化为 Flow；当变换是线性的，VFlow 退化为 VAE。

Flow 的初衷为效果比 VAE 更好的显式模型，但其结构限制了性能。为此，VFlow 松弛了其显式表达，引入变分来将 Flow 的性能进一步提升。

Implicit Normalizing Flow - ImpFlow

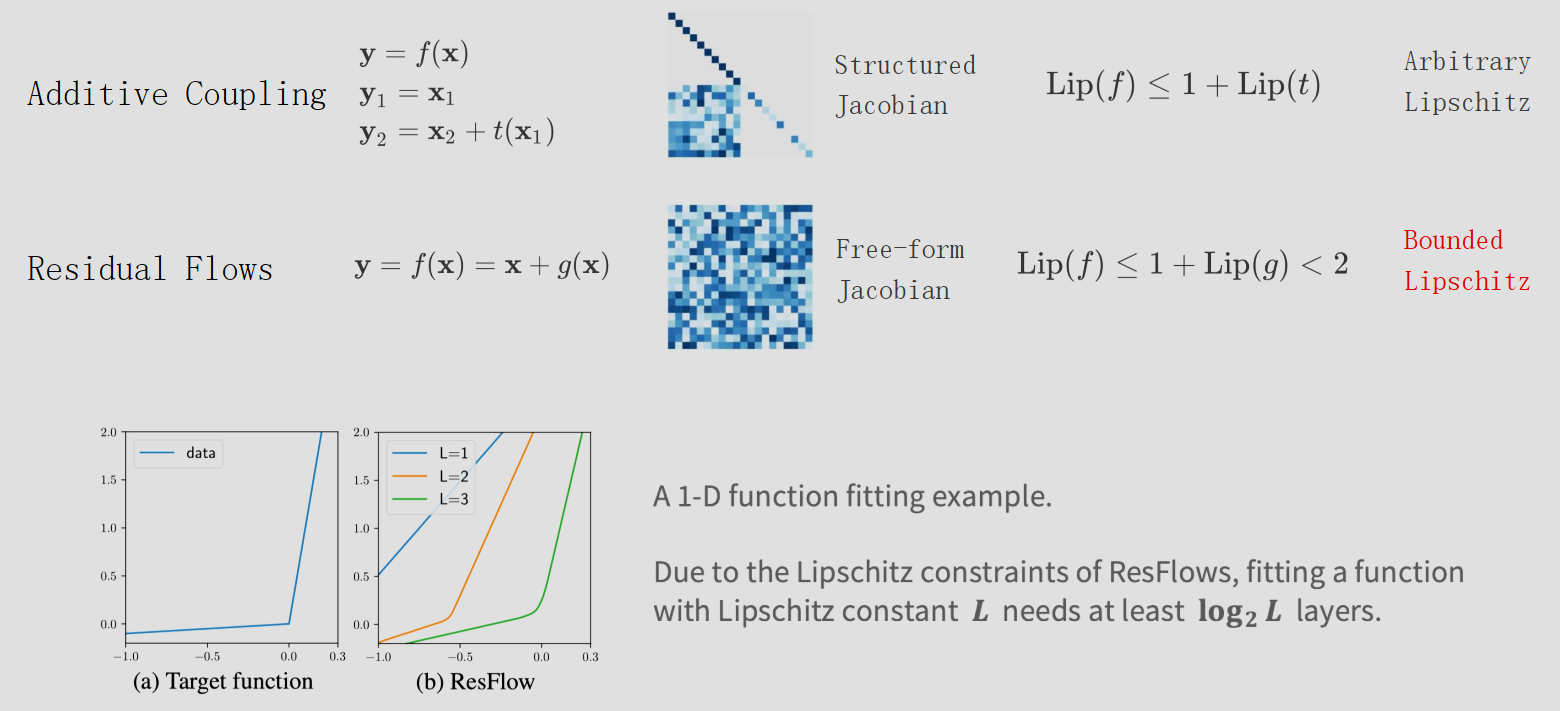
何凯明 Resnet 的残差结构效果十分惊人，但直接添加不可逆，无法引入到流模型。可逆的残差结构 i-ResNet 要求 Lipschitz 常熟严格小于 1（变换不能过于剧烈），这导致了模型的表达能力受限。

为此，与其显式的定义 \(z=f(x)\)，直接定义方程 \(F(z,x)=0\)。隐函数定理保证了非奇异 \(\partial F / \partial z\) 的可逆性。

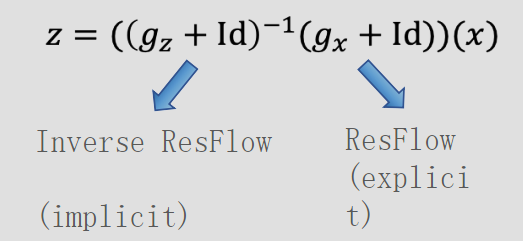
ImpFlow 可以看作是一个 ResFlow 和一个逆 ResFlow 的复合。

推理阶段使用不动点迭代（Fixed Point Iteration）或 Broyden 方法来解方程 \(F(z,x)=0\)。

找固定点： \[ z = ((g_z + Id)^{-1}(g_x + Id))(x) \] 训练阶段使用隐函数求导法则直接算出 \(\partial z / \partial x\)，不需要保存所有中间迭代状态。

Jacobian 的 log-determinant： \[ \ln p(\mathbf{x}) = \ln p(\mathbf{z}) + \ln \det(I + J_{g_{\mathbf{x}}}(\mathbf{x})) - \ln \det(I + J_{g_{\mathbf{z}}}(\mathbf{z})) \] BP： \[ \frac{\partial \mathcal{L}}{\partial \mathbf{z}} \frac{\partial \mathbf{z}}{\partial (\cdot)} = \frac{\partial \mathcal{L}}{\partial \mathbf{z}} J_{G}^{-1}(\mathbf{z}) \frac{\partial F(\mathbf{z}, \mathbf{x}; \theta)}{\partial (\cdot)} , \text{ where } G(\mathbf{z}; \theta) = g_{\mathbf{z}}(\mathbf{z}; \theta) + \mathbf{z}. \]

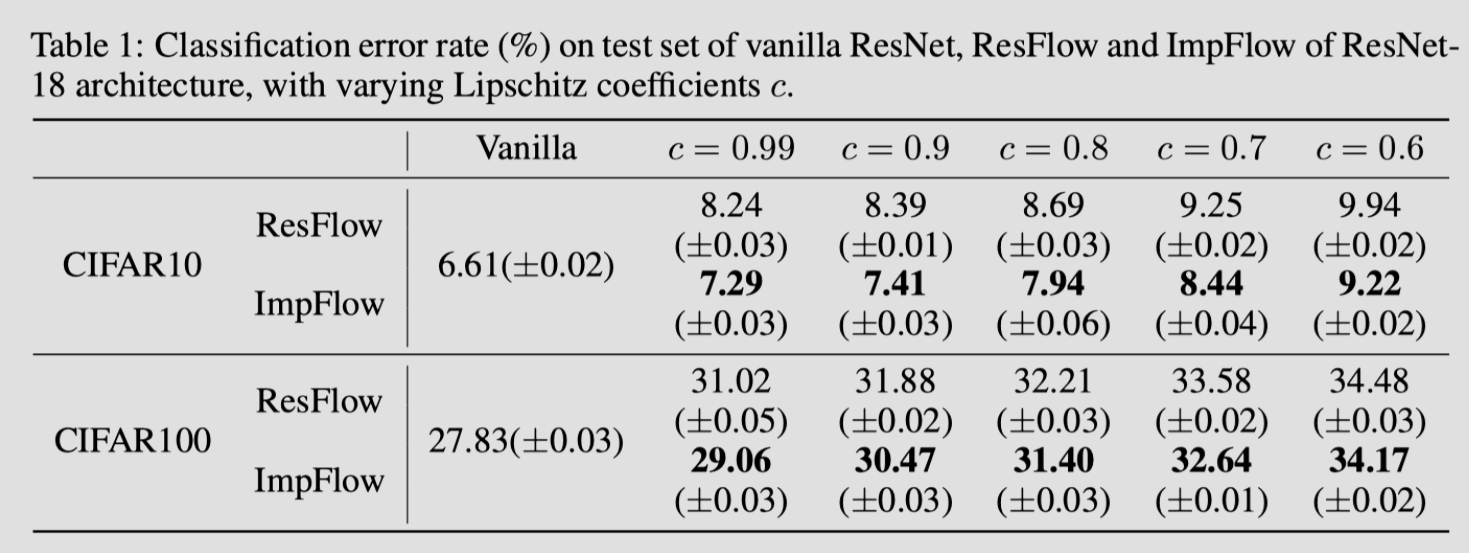
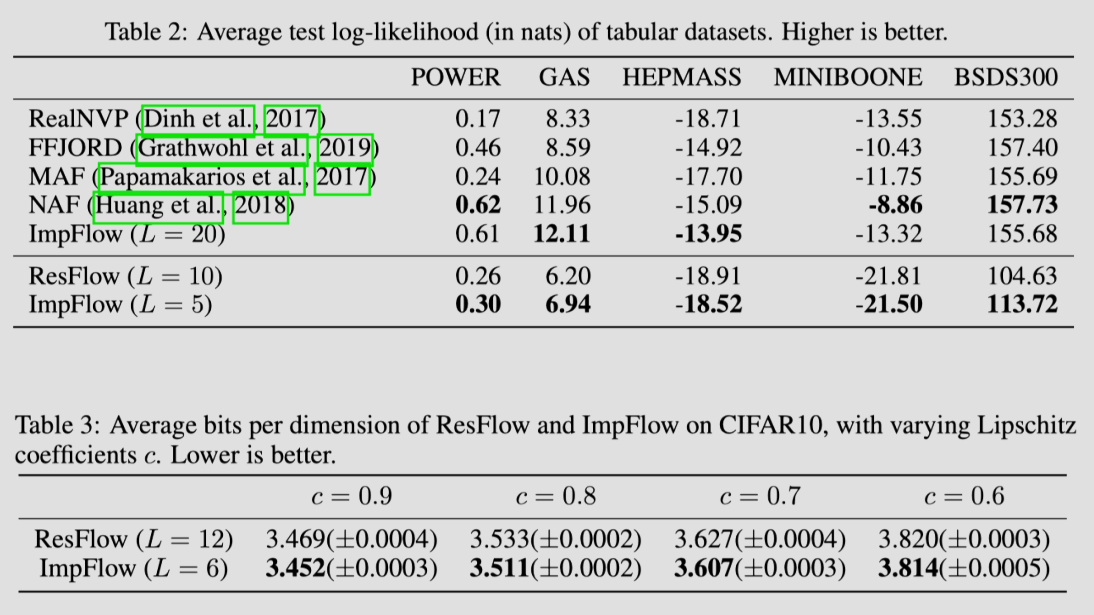
可以看到效果比 ResFlow 提升许多。

流匹配：Flow Matching

Flow (Normalizing Flow) 和 Flow Matching (FM) 的关系可以类比为“一种模型类别”与“一种高效的训练方法”。

虽然它们都属于“流模型”的大范式，但 Normalizing Flow 侧重于利用可逆变换和变量替换公式来显式建模概率密度；而 Flow Matching 则是一种现代的、无需模拟（Simulation-free）的训练框架，专门用于解决连续流模型（CNF）训练慢、约束多的痛点。

1. 核心要点概括

• Flow (Normalizing Flow)： 是一类生成模型的总称。它通过一系列可逆函数 \(f\) 将简单分布（如高斯）映射到复杂数据分布。其核心数学工具是变量替换公式 (Change of Variables)。
• Flow Matching (FM)： 是一种训练算法/目标函数。它允许我们在不运行 ODE 求解器的情况下，直接训练一个连续时间流模型。它将生成过程看作是沿着向量场 (Vector Field) 的运动，并让神经网络去“匹配”这个向量场。

---

2. Normalizing Flow (NF)：经典的显式概率模型

在传统的（离散步长的）正规化流模型（如 RealNVP, Glow）中，每一层的变换必须满足：

1. 必须是双射（可逆）： 这样才能从噪声生成数据，也能从数据推回噪声。
2. 雅可比行列式（Jacobian）易计算： 为了计算似然函数 \(p(x)\)。

数学公式：

\[p(x) = p(z) \left| \det \frac{\partial f^{-1}}{\partial x} \right|\]

局限性： 这种强加的可逆性和雅可比约束极大地限制了神经网络的结构设计（例如只能用特定的 Coupling Layer），导致模型表达力受限，且在高维数据上计算开销巨大。

---

3. Flow Matching (FM)：现代的、直线化的训练方案

Flow Matching 针对的是连续时间流模型 (Continuous Normalizing Flow, CNF)。在 CNF 中，样本的演化由一个常微分方程 (ODE) 描述：\(\frac{dx}{dt} = v_t(x)\)。

Flow Matching 的创新之处在于：

• 无需 ODE 模拟： 传统 CNF 训练时需要调用 ODE Solver（如 adjoint method），速度极慢。FM 提出了一种“模拟无关”的损失函数。
• 匹配向量场： 它预定义一个概率路径（通常是噪声和数据之间的直线插值），计算出该路径对应的理想向量场 \(u_t(x)\)，然后训练网络 \(v_{\theta}\) 去预测它。

数学目标（简化的 MSE）：

\[\mathcal{L}_{FM}(\theta) = \mathbb{E}_{t, x_t} [ \| v_{\theta}(x_t, t) - u_t(x_t | x_1) \|^2 ]\]

为什么它现在很火？

因为它解决了扩散模型（Diffusion）路径“弯曲”的问题。通过 Rectified Flow（修正流） 等技术，FM 可以学习到从噪声到数据的直线路径。路径越直，推理时需要的步数就越少（甚至 1 步生成）。

---

4. 两者的关键区别对比

特性	Normalizing Flow (传统)	Flow Matching (现代)
模型性质	离散步长的可逆映射组合	连续时间的常微分方程 (ODE)
训练目标	最大化对数似然 (NLL)	最小化向量场预测误差 (MSE)
网络约束	必须设计特殊的可逆结构	无约束（可用普通 Transformer/U-Net）
路径形状	复杂、由网络结构决定	可以人为定义（如直线）
代表作	RealNVP, Glow	Stable Diffusion 3, Flux.1

---

5. 总结：它们是如何融合的？

在 2024-2025 年的最前沿模型中（如 Stable Diffusion 3 和 Flux），我们看到的其实是：

1. 使用 VAE 将图像压缩到隐空间。
2. 在隐空间使用 Flow Matching 框架进行训练。
3. 通过 Rectified Flow 确保路径是直的。
4. 利用 Transformer (DiT) 作为底层的向量场预测网络。

这种组合兼具了 Flow 的确定性、Diffusion 的稳定性以及直线路径的高效性。

修正流：Rectified Flow

Rectified Flow (修正流) 是由刘铁岩团队（Xingchao Liu 等）提出的一种新型生成模型框架。它是 Flow Matching 思想的一种最简洁、最直观的实现方式，目前已成为 Stable Diffusion 3 (SD3) 和 Flux.1 等顶级模型的核心技术。

1. Rectified Flow 的核心要点概括

• 核心理念： 放弃扩散模型那种弯曲、随机的去噪路径，强制要求模型沿着直线轨迹从噪声演化到数据。
• 数学形式： 采用最简单的线性插值 (Linear Interpolation) 来连接噪声点和数据点。
• 核心优势：
  • 推理极快： 因为路径是直的，可以用极少的步数（甚至 1 步）完成采样，且误差极小。
  • 理论优雅： 统一了 Diffusion 和 Flow，将复杂的 SDE（随机微分方程）简化为简单的直线 ODE（常微分方程）。
  • 架构无关： 底层可以随意更换为 Transformer (DiT) 或 U-Net。

---

2. 核心原理：为什么是“直线”？

在传统的扩散模型（如 DDPM）中，加噪和去噪的过程遵循复杂的概率曲线，这导致模型在推理时必须小心翼翼地走很多小碎步（采样步数多），否则就会偏离轨道。

Rectified Flow 重新定义了这个过程：

(1) 线性插值 (The Bridge)

给定一个噪声图像 \(x_0 \sim N(0, I)\) 和一张真实图像 \(x_1 \sim P_{data}\)，Rectified Flow 定义了一条最简单的直线路径 \(X_t\)：

\[X_t = t x_1 + (1 - t) x_0\]

这里的 \(t \in [0, 1]\)。当 \(t=0\) 时是纯噪声，当 \(t=1\) 时是纯图片。

(2) 训练目标 (Velocity Matching)

既然路径是直线，那么在任何时刻 \(t\)，样本演化的“速度”（方向）就是一个定值：

\[\frac{dX_t}{dt} = x_1 - x_0\]

我们训练一个神经网络 \(v_\theta(X_t, t)\)，它的唯一任务就是预测这个恒定的速度：

\[\min_\theta \mathbb{E}_{x_0, x_1, t} [ \| v_\theta(X_t, t) - (x_1 - x_0) \|^2 ]\]

---

3. “1-Rectified Flow” 与 Reflow（路径直化）

虽然我们用直线公式训练模型，但在复杂的概率分布中，不同样本的路径可能会交叉。交叉会导致模型在采样时产生混淆（一个点可能对应多个方向），从而使路径变弯。

为了解决这个问题，Rectified Flow 引入了 Reflow 操作：

1. 第一阶段： 训练一个基础模型（称为 1-Rectified Flow）。

2. 第二阶段 (Reflow)： 用训练好的模型生成一批“合成数据对” \((x_0, \hat{x}_1)\)。因为这些对是由模型生成的，它们在某种程度上已经“解耦”了。

3. 第三阶段： 用这些合成数据对重新训练模型。

   经过 Reflow 后的模型，其向量场几乎是完全直线的。这意味着你从噪声出发，只需要计算一次 \(v_\theta\)，然后大步跨过去，就能得到高质量的图像。

---

4. 为什么 Stable Diffusion 3 要用它？

在 SD1.5 或 SDXL 时代，模型是基于 噪声预测 (Noise Prediction) 的。而在 SD3 中，何恺明参与的 DiT 架构结合了 Rectified Flow：

• 信噪比平衡： 线性插值在 \(t\) 的整个区间内分配得非常均匀，不像传统扩散模型那样在某些阶段噪声占绝对主导，导致学习效率低。
• 高分辨率优势： 在处理 1024x1024 甚至更高的分辨率时，直线的 ODE 轨迹比弯曲的扩散轨迹更容易捕捉高频细节。
• 采样效率： 结合 Flow Matching 后的 SD3，在 10-20 步时的效果就已经超过了以前模型 50 步的效果。

---

5. 总结对比：RF vs. Diffusion

特性	传统扩散模型 (DDPM/LDM)	Rectified Flow (SD3/Flux)
路径形状	弯曲的轨迹 (Curved)	直线轨迹 (Straight)
演化方程	随机微分方程 (SDE)	常微分方程 (ODE)
预测目标	预测噪声 \(\epsilon\)	预测速度 \(v\) (或方向)
推理步数	通常需要 30-50 步	5-15 步即可（甚至 1 步）
数学美感	依赖变分推导	简单的两点插值

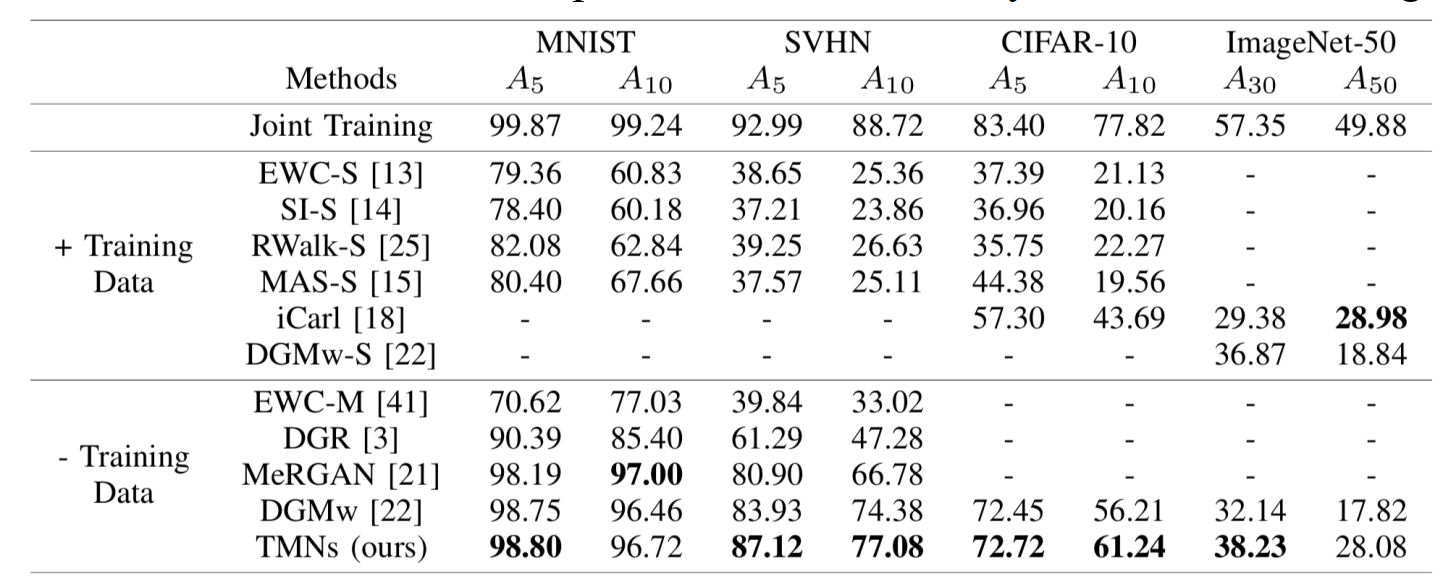
半监督 GAN：Triple-GAN

传统的 GAN 主要用于无监督学习（生成图片）。为了利用 GAN 进行半监督学习 (Semi-supervised Learning, SSL)，即利用少量有标签数据和大量无标签数据来提升分类精度，Triple-GAN 提出了一种全新的博弈框架。

Triple-GAN 引入了一个额外的玩家：分类器 C。

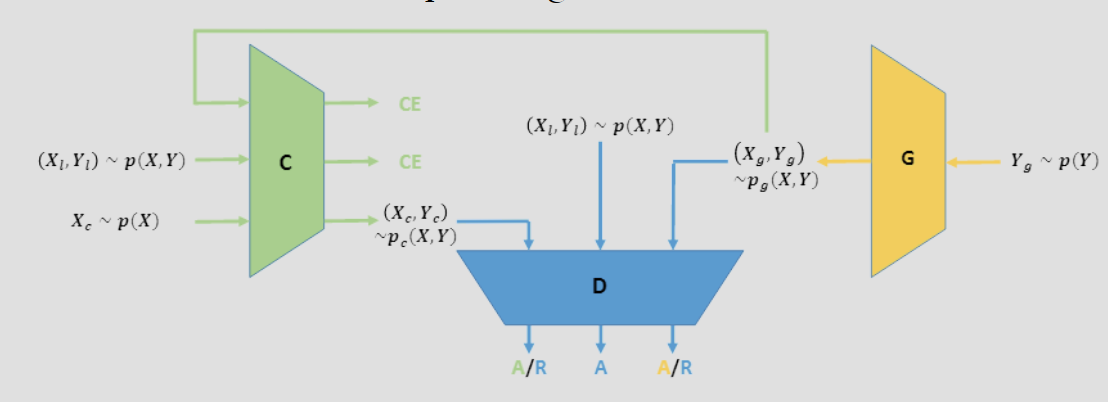
分类器 (C)：

• 角色：给定真实数据 \(x\)，生成伪标签 \(y\)。
• 分布：\(P_C(x, y) = P(x) P_C(y|x)\)。

生成器 (G)：

• 角色：给定标签 \(y\)，生成伪数据 \(x\)（条件生成）。
• 分布：\(P_G(x, y) = P(y) P_G(x|y)\)。

判别器 (D)：

• 角色：它不再只分辨 \(x\) 的真假，而是分辨“数据-标签对” \((x, y)\) 的来源。它需要判断一个 \((x, y)\) 对是来自真实数据集，还是来自 C 生成的，或者是来自 G 生成的。

优化问题为： \[ \min_{C,G} \max_{D} U(C,G,D) := E_{P_{data}}[\log D(x,y)] + \alpha E_{P_C}[\log(1-D(x,y))] + (1-\alpha) E_{P_G}[\log(1-D(x,y))] \] 其中超参数 \(\alpha\) 一般为 \(1/2\)。还能引入损失函数： \[ \min_{C,G} \max_{D} \tilde{U}(C,G,D) := U(C,G,D) + E_{p_{\text{data}}}[-\log p_C(y|x)] \] 可被证明，达到纳什均衡当且仅当 \(P(x, y) = P_G(x, y) = P_C(x, y)\)，与 \(D^*_{C,G}(x,y)=\frac12\)。也就是，C 变成了一个完美的分类器，G 变成了一个完美的条件生成器。

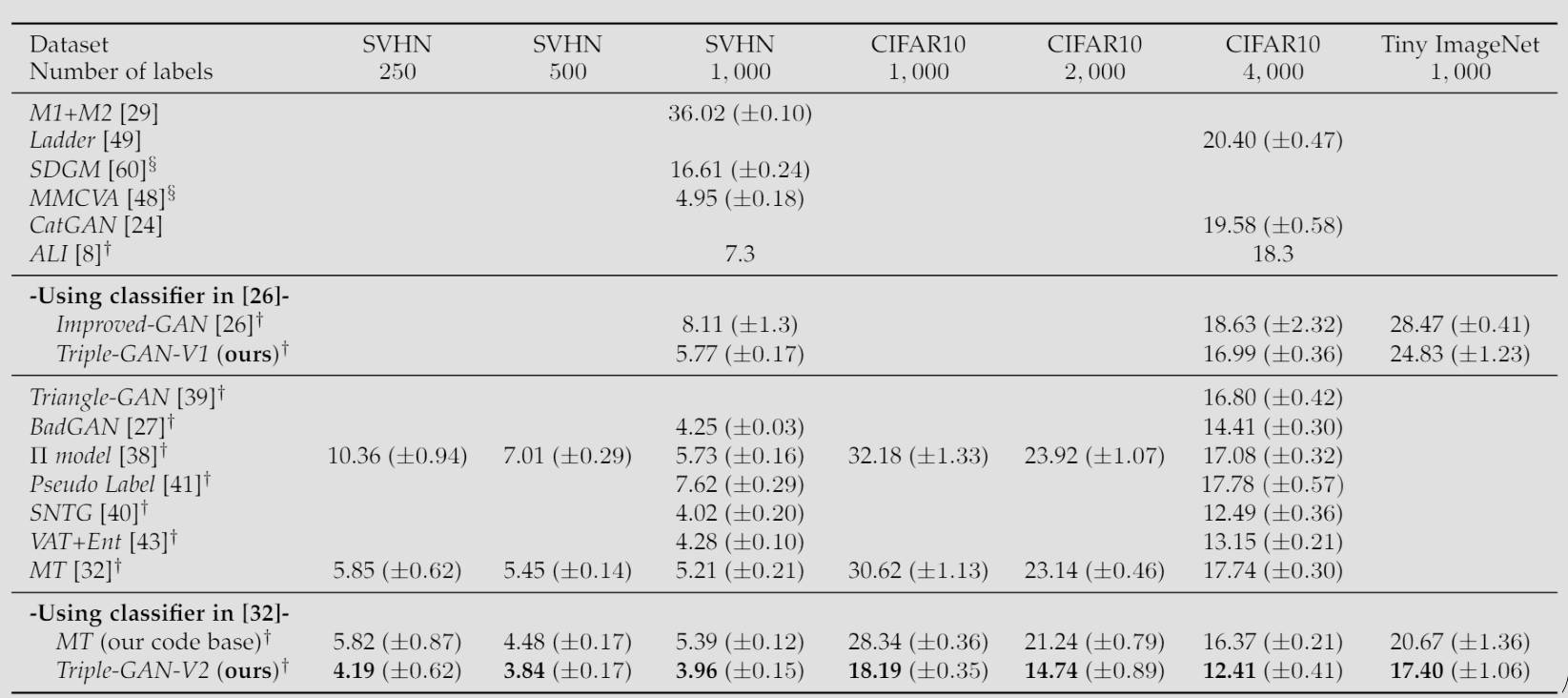
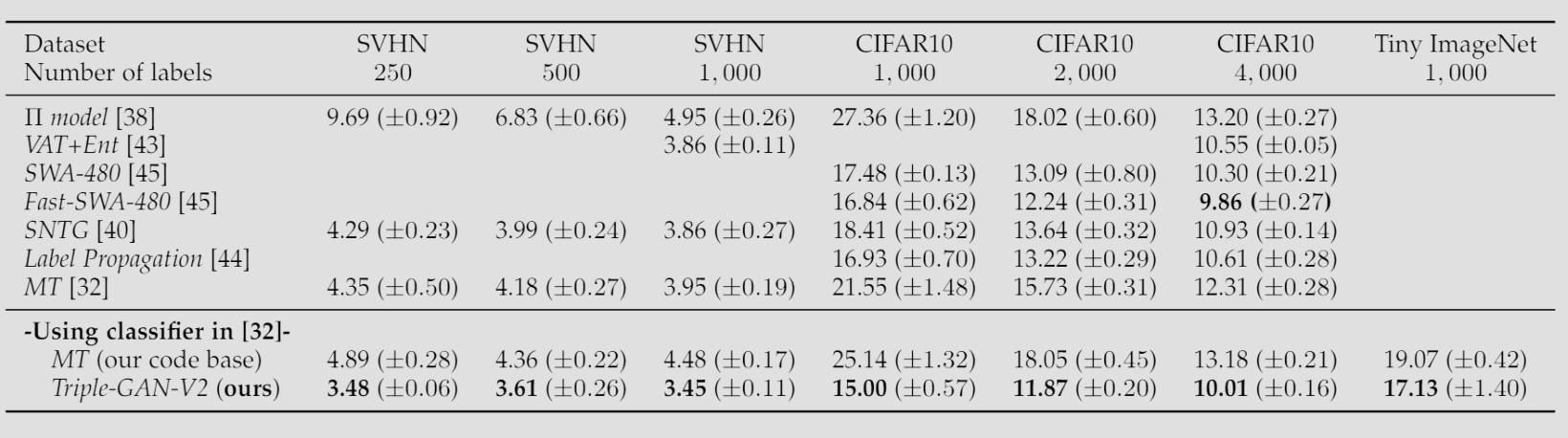
持续学习模型：Triple Memory Networks

背景与动机：

深度学习模型通常面临“灾难性遗忘” (Catastrophic Forgetting) 问题——学了新任务，旧任务就忘了。人类大脑却能终身学习。

生物学启发 (Brain Inspiration)：

该模型模拟了大脑记忆系统的双重编码理论：

• 海马体 (Hippocampus)：负责快速学习，存储具体经验 (Specific Experience)。
• 新皮层 (Neocortex)：负责慢速巩固，存储泛化知识 (Generalized Knowledge)。
• 记忆回放 (Memory Replay)：海马体会将短期记忆“回放”给新皮层，使其转化为长期稳定的知识。

模型架构与机制：

Triple Memory Networks (TMN) 并没有真的去存原始数据（那样太占空间且隐私不安全），而是用生成模型来模拟“海马体”：

1. 生成记忆 (Generative Memory / G)：
   • 对应“海马体”。每学一个新任务，就训练一个简单的生成器来记住这个任务的数据分布。
   • 在学习新任务时，它可以生成旧任务的“伪数据”进行回放。
2. 推断记忆 (Inference Memory / Classifier)：
   • 对应“新皮层”。这是一个用于分类的主网络。
   • 它通过不断接收来自真实新数据和 G 生成的旧数据的混合训练，来实现知识的巩固。
3. 具体的做法：
   • 当学习任务 \(t\) 时，模型不仅用当前数据训练，还让 G 生成任务 \(0\) 到 \(t-1\) 的数据一起训练。这被称为“伪回放” (Pseudo-Replay)。

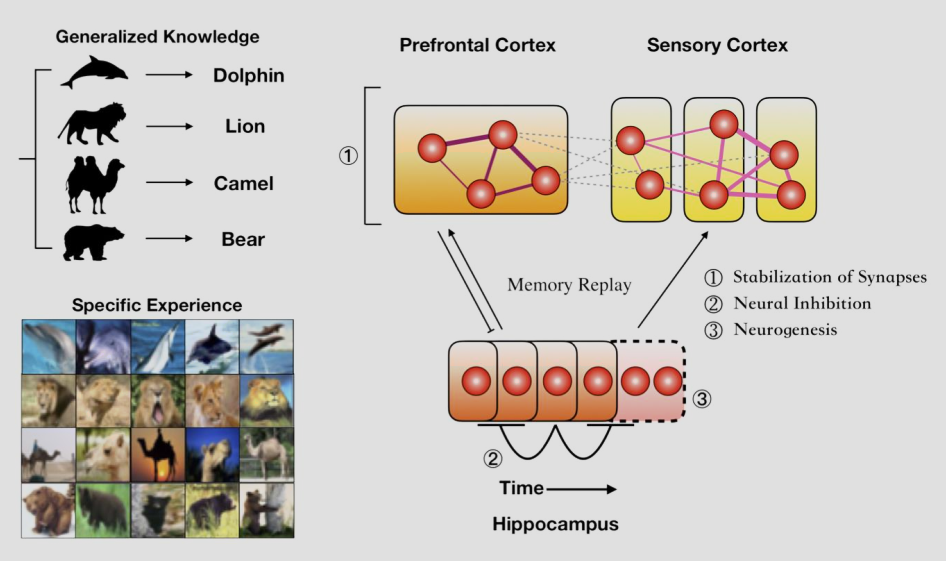
优势：

TMN 在不访问旧的真实数据（隐私友好）的前提下，在 CIFAR-10 和 ImageNet 等数据集的持续学习任务上取得了极佳的效果，有效避免了遗忘。

自回归模型 Auto-Regressive Deep Generative Model

基础 AR 与参数量

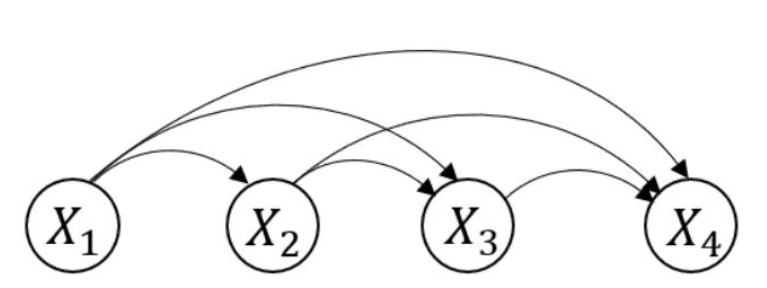
考虑序列数据 \(x=(x_1,...,x_d)\)。AR 模型利用概率的链式法则 (Chain Rule)，将高维数据的联合分布 \(p(x)\) 分解为一系列条件概率的乘积：

\[p(x) = \prod_{i=1}^{d} p(x_i | x_1, \dots, x_{i-1}) = \prod p(x_i | x_{<i})\]

这意味着生成过程是序列化的：生成第 \(i\) 个像素（或单词）时，依赖于之前生成的所有内容。

但直接对 \(p(x_i|x_{<i})\) 的每个乘积建模数量过多（指数级），如果假设分布为 Bernoulli，可以仅对其参数 \(\theta\) 进行建模。

• Sigmoid belief network \(f_i =\sigma(\alpha_1^{(i)}x_1+\alpha_2^{(i)}x_2+...+\alpha_{i-1}^{(i)}x_{i-1})\) 的参数量为 \(\sum_{i=1}^d i = O(d^2)\)。
• MLP \(h_i=\sigma(A_i x_{<i}+b_i), f_i(x_1,...,x_{i-1})=\sigma(\alpha_i^\top h_i + c_i)\) 的参数两为 \(O(d^2L)\)。
• Neural Auto-regressive Density Estimator （NADE）通过共享隐藏层权重 \(W\) 和偏置 \(b\)：\(h_i=\sigma(W_{.,<i} x_{<i}+b), f_i(x_1,...,x_{i-1})=\sigma(\alpha_i^\top h_i + c_i)\) 将参数两降低为 \(O(dL)\)。对于连续变量，可以通过 MoG 混合高斯模型进行建模。

词嵌入

降维 - alittlebear’s blog

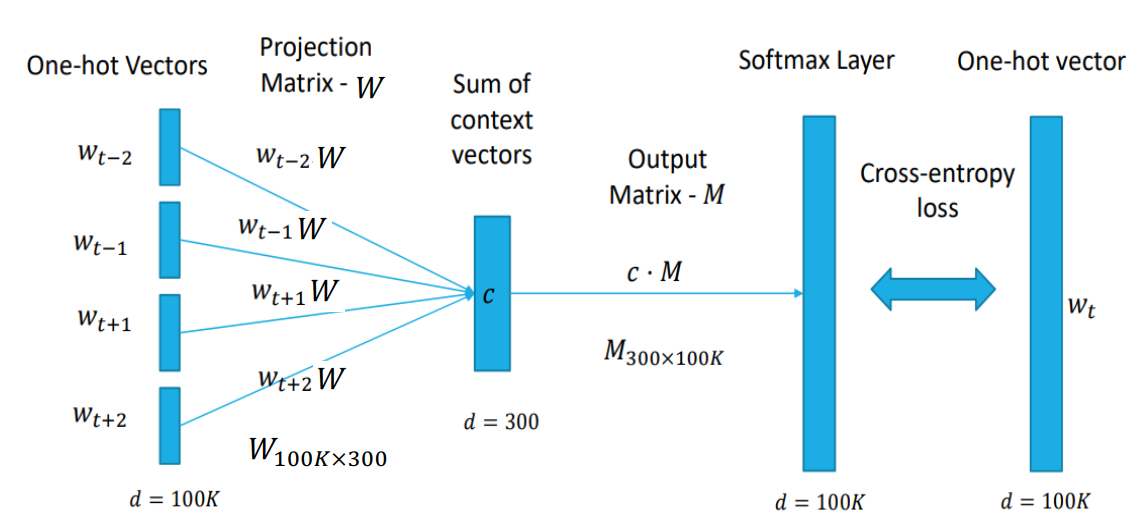
CBOW：

Skip-gram：

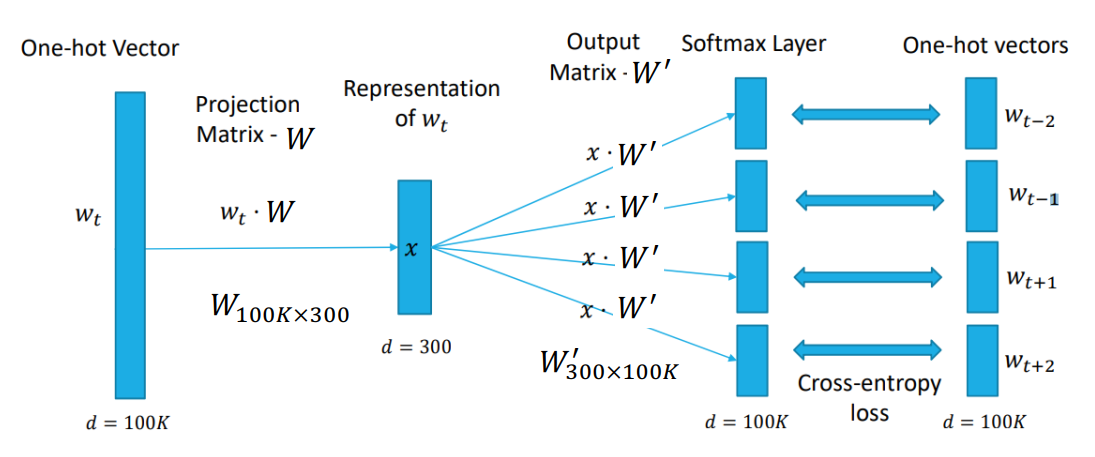
Word2Vec：

• CBOW (Continuous Bag-of-Words)：通过上下文（周围的词）来预测中间的词。
• Skip-gram：通过中间的词来预测周围的上下文。
• 原理：Skip-gram 为每个词学习两个向量（输入向量 \(v\) 和输出向量 \(v'\)）。模型的目标是最大化正样本对的共现概率。

负采样 (Negative Sampling)：

• 痛点：计算 Softmax 分母需要遍历词表中所有单词（如 10 万个），计算量太大。
• 解决方案：将多分类问题转化为二分类问题。对于每一对“真”的词对 \((w_t, w_{t+j})\)，随机采样 \(k\) 个“假”的词（噪声）。
• 优化目标：最大化真词对的 Sigmoid 概率，同时最小化假词对的 Sigmoid 概率。这在数学上等价于对互信息（PMI）的矩阵分解 (p. 23-24)。

语言模型

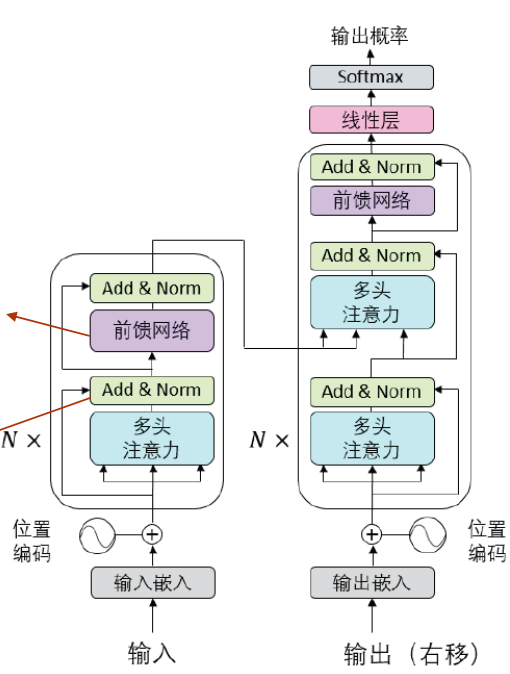
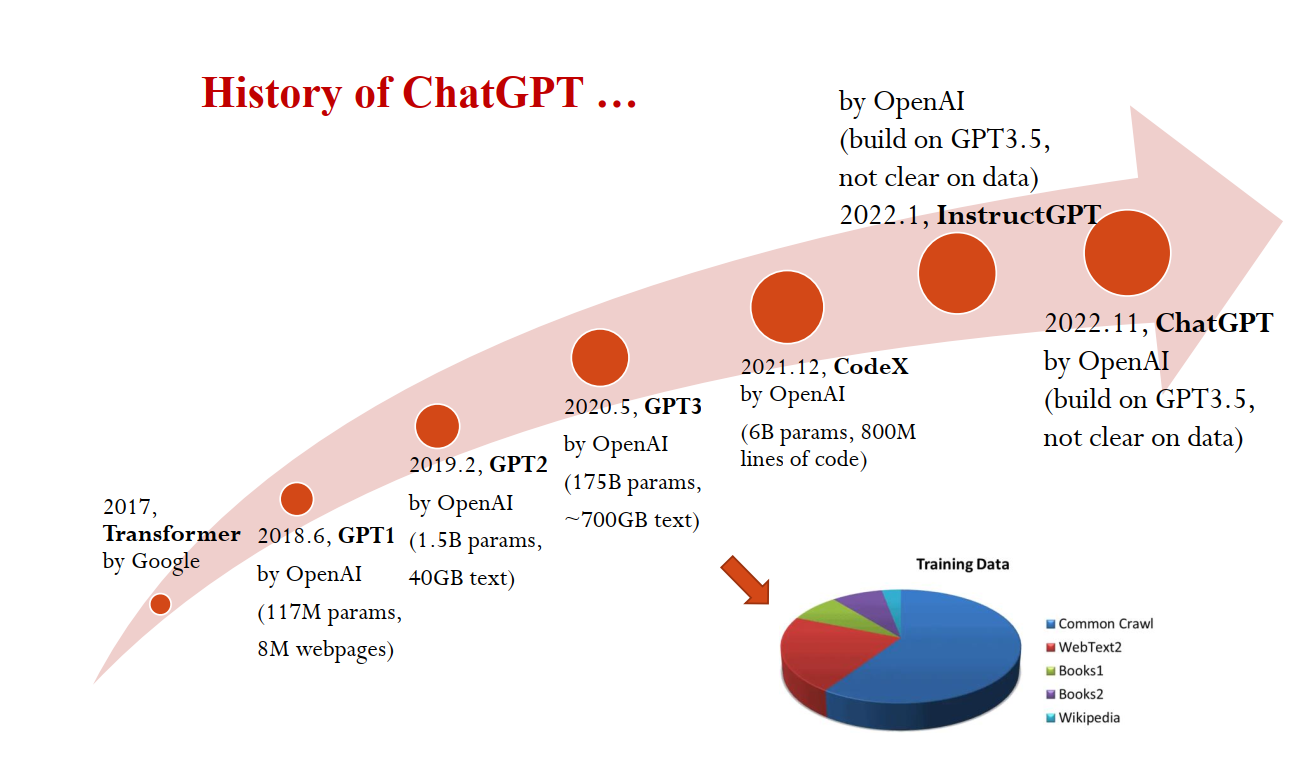
现在（早期）的大语言模型都是 AR 模型，主要分为三个流派。

参考：Transformer - alittlebear’s blog

扩散模型 Diffusion Probabilistic Model（DPM）

去噪扩散模型 Denoising Diffusion Probabilistic Model（DDPM）

扩散随时间破坏整体结构，但如果我们可以逆转这个过程呢？

扩散过程先逐渐给数据添加噪声：

这个过程可以用马尔科夫链描述（每一步仅依赖于上一步）：\(q(x_0,...,x_N)=q(x_0)q(x_1|x_0)...q(x_N|x_{N-1})\)，其中 \(q(x_n|x_{n-1})=\mathcal{N}(\sqrt{\alpha_n}x_{n-1},\beta_n I), \alpha_n=1-\beta_n\)，并最终趋于标准正态分布 \(x_N\approx \mathcal{N}(0,1)\)。

然后，反方向进行去噪：\(q(x_0,...,x_N)=q(x_0|x_1)...q(x_{N-1}|x_N)q(x_N)\)

上述是理想情况。实际上模型用 \(p(x_{n-1}|x_n)=\mathcal{N}(\mu_n(x_n),\sigma^2_nI)\) 来模拟 \(q(x_{n_1}|x_n)\)，也就是，模型的去噪过程为 \(p(x_0,...,x_N)=p(x_0|x_1)...p(x_{N-1}|x_N)p(x_N)\)。

扩散模型简单且性能十分出色。相比 VAE 不需要学习 Encoder 来加密图像（添加噪声不需要学习）；训练目标就是 MSE 平均差： \[ \frac{1}{2} \int_{0}^{T} \omega(t) \mathbb{E}_{q_0(\mathbf{x}_0)} \mathbb{E}_{q(\boldsymbol{\epsilon})} \left[ \| \boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) - \boldsymbol{\epsilon} \|_2^2 \right] \mathrm{d}t \] 也就是，网络 \(\epsilon_\theta\) 的任务是看一眼加噪后的图 \(x_t\) 和时间 \(t\)，然后猜测刚才加进去的噪声 \(\epsilon\) 长什么样。

并且，对于足够多的迭代次数，反方向保证了是高斯【也就是，如果我们将前向加噪过程切分得足够细（\(T\) 很大，每步加入的噪声 \(\beta_t\) 极小），那么原本极其复杂的逆向分布 \(q(x_{t-1}|x_t)\) 就会退化为一个简单的辅助高斯分布。】

总结一下，扩散模型分为两个阶段：

训练阶段（前向过程）：

• 加噪：从真实图像 \(x_0\) 开始，按照预设的规则逐步加入高斯噪声，直到图像变成纯噪声 \(x_T\)。
• 学习：训练一个神经网络 \(\epsilon_\theta\)（通常是 U-Net），让它学习在任何一个时刻 \(t\) 的加噪图像 \(x_t\) 中，预测刚才加入的那个“噪声”是什么。

生成阶段（逆向过程）：

• 初始化：从一个标准的正态分布噪声 \(x_T \sim \mathcal{N}(0, I)\) 开始。
• 迭代去噪：利用训练好的神经网络预测噪声，并一步步将其减去，最终还原出一张图像。

连续时间扩散模型

理论上可以将这个离散过程取极限变为连续过程：

前向过程将数据变噪声，后向过程将噪声变数据。两者在数学上描述的是同一条“路径”，只是时间流向相反。

在随机微分方程（SDE）的理论中，如果一个前向 SDE 描述了概率密度 \(p(x, t)\) 随时间演化的过程，那么一定存在一个对应的后向 SDE，能够精准地沿着原路折返。

这个结论由 Brian Anderson 在 1982 年证明。他指出：如果我们希望后向 SDE 生成的路径轨迹与前向 SDE 录像倒放的结果一致，那么后向 SDE 的漂移项必须包含得分函数（Score Function）。

Denoising Diffusion Implicit Model（DDIM）：从 SDE 到 ODE

从分布 \(q_0(x_0)\) 开始，如果将分布 \(q_t(x_t)\) 定义为随机微分方程 SDE 函数： \[ \mathrm{d}\boldsymbol{x}_t = \boldsymbol{f}(\boldsymbol{x}_t, t)\mathrm{d}t + g(t)\mathrm{d}\boldsymbol{w}_t \] 那么，可以证明这个 ODE 的边缘分布与 \(q_t(x_t)\) 一致： \[ \frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t} = \boldsymbol{f}(\boldsymbol{x}_t, t) - \frac{1}{2}g(t)^2 \nabla_{\boldsymbol{x}} \log q_t(\boldsymbol{x}_t) \] 这表示了可以不通过带随机性的 SDE 采样，而是通过解一个确定的 ODE 来得到同样符合数据分布的样本。基于此，DDPM 衍生出了 DDIM 通过求解 ODE 而不是 SDE 来加快采样速度与精度，但因其确定性，不可避免地失去了输出的多样性与稳健性：

维度	DDPM (Denoising Diffusion Probabilistic Models)	DDIM (Denoising Diffusion Implicit Models)
数学基础	随机微分方程 (SDE)：包含随机项 \(g(t)d\bar{\mathbf{w}}_t\)	常微分方程 (ODE)：只有确定性的偏移项
生成过程	随机性。同一个初始噪声通过多次运行会得到不同的图像。	确定性。一旦初始噪声 \(\mathbf{x}_T\) 固定，生成的图像 \(\mathbf{x}_0\) 也就完全固定。
采样步数	慢。通常需要 1000 步采样。	快。支持跳步（Sub-sampling），只需 20-50 步即可达到较好效果。
可逆性	不可逆。因为每一步都加入了新的随机噪声。	可逆。由于是 ODE 轨迹，可以将图像编码回噪声空间再还原。
训练方式	需要从头训练预测噪声 \(\boldsymbol{\epsilon}_\theta\) 的网络。	无需重新训练。直接使用 DDPM 训练好的模型权重即可。

更具体的，DDPM（Denoising Diffusion Probabilistic Models）的采样等价于对这个 SDE 的一阶离散化求解： \[ d\mathbf{x}_t = \underbrace{\left[f(t)\mathbf{x}_t + \frac{g^2(t)}{\sigma_t}\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t)\right] dt}_{\text{确定性漂移 (Drift)}} + \underbrace{g(t)d\bar{\mathbf{w}}_t}_{\text{随机扩散 (Diffusion)}} \] 这意味着 DDPM 每次生成的图都不一样，是因为它在还原路径上不断地进行随机“抖动”。

SDE 公式中的随机项：\(g(t)d\bar{\mathbf{w}}_t\) 是导致每次生成结果不同的根本原因。

还原路径：在 DDPM 的每一步还原中，模型不仅根据 \(\boldsymbol{\epsilon}_\theta\) 预测的方向移动（确定性漂移），还会注入一个随机的高斯扰动。

结果影响：由于路径上充满了这种随机分叉，即使从同一个初始噪声起点出发，DDPM 最终也会降落在数据分布中的不同点（即生成不同的图片）。

并且，用（ODE求解的） DDIM 采样本质上对应了以下 ODE 的一阶离散化求解： \[ \frac{d\mathbf{x}_t}{dt} = f(t)\mathbf{x}_t + \frac{g^2(t)}{2\sigma_t}\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t) \] 仅用一阶信息数学上还是不够快，下面可以看到如何通过更多信息（更高阶信息）加速采样过程。

轨迹的确定性：在 DDPM 的 SDE 框架下，由于每一步都有随机扰动，如果步长过大，误差会迅速积累导致崩溃。

ODE 求解器：DDIM 将问题转化为了求解 \(\frac{d\mathbf{x}_t}{dt}\)。在数学上，ODE 的轨迹是平滑的，这意味着我们可以使用更大的步长（即跳过中间的时间点）来近似整条曲线，而不会偏离原始分布。

Analytic-DPM：DPM 的最优反向方差估计

Analytic-DPM 优化了原 DDPM 对于方差的假设/估计，实际优化也适用于 ODE 的 DDIM。

在前面，模型用 \(p(x_{n-1}|x_n)=\mathcal{N}(\mu_n(x_n),\sigma^2_nI)\) 来模拟实际分布 \(q(x_{n_1}|x_n)\)，这之前是通过最小化 KL 散度（最大化 ELBO）来解决的： \[ \overset{\text{min KL}}{\min_{\mu_n(\cdot), \sigma_n^2} KL(q(x_{0:N}) \| p(x_{0:N}))} \iff \overset{\text{max ELBO}}{\max_{\mu_n(\cdot), \sigma_n^2} \mathbb{E}_q \log \frac{p(x_{0:N})}{q(x_{1:N}|x_0)}} \Rightarrow \underset{\substack{\uparrow \\ \text{DDPM only optimizes the model mean} \\ \text{Use handcrafted model variance, e.g., } \sigma_n^2 = \beta_n}}{\overset{\text{Reweighted ELBO (Score matching)}}{\min_{s_n(\cdot)} \mathbb{E}_n \bar{\beta}_n \mathbb{E}_{q_n(x_n)} \| s_n(x_n) - \nabla \log q_n(x_n) \|^2}} \] 上述重加权的 ELBO 不再直接预测分布均值 \(\mu_n\)，而是预测得分函数 \(s_n\)，再通过这个参数化公式计算出 \(\mu_n\)： \[ \mu_n(x_n) = \frac{1}{\sqrt{\alpha_n}}(x_n + \beta_n s_n(x_n)) \] 但这是次优解，目标函数只是优化了模型均值 \(\mu_n\)。对于方差 \(\sigma_n^2\)，DDPM 直接使用了人工设定的值（如 \(\sigma_n^2 = \beta_n\)），而不是让模型去学习它；DDIM 直接设置为 0 （确定性采样）；Improved DDPM 让网络去学习方差（难以训练）。

基于此，Analytic-DPM 直接证明了反向方差的解析解（证明用到了矩匹配，总方差定理，等）：\(\min_{\mu_n(\cdot), \sigma_n^2} KL(q(x_{0:N}) \| p(x_{0:N}))\) 的最优解是： \[ \mu_n^*(x_n) = \frac{1}{\sqrt{\alpha_n}} (x_n + \beta_n \nabla \log q_n(x_n)), \]

\[ \sigma_n^{*2} = \frac{\beta_n}{\alpha_n} \left( 1 - \beta_n \mathrm{E}_{q_n(x_n)} \frac{\| \nabla \log q_n(x_n) \|^2}{d} \right). \]

这里 $_{q_n(x_n)} $ 可以通过蒙特卡洛法来近似得到。

基于此解析解，还能得到方差的上限：\(\sigma_n^{*2}\) 的上下界为： \[ \tilde{\beta}_n \leq \sigma_n^{*2} \leq \frac{\beta_n}{\alpha_n} \] 如果进一步假设数据分布有界（存在界 \([a,b]^d\)，这里 \(d\) 是数据的维度），那么上界可以缩小到： \[ \sigma_n^{*2} \leq \tilde{\beta}_n + \frac{\bar{\alpha}_{n-1}\beta_n^2}{\bar{\beta}_n^2} \left(\frac{b-a}{2}\right)^2. \]

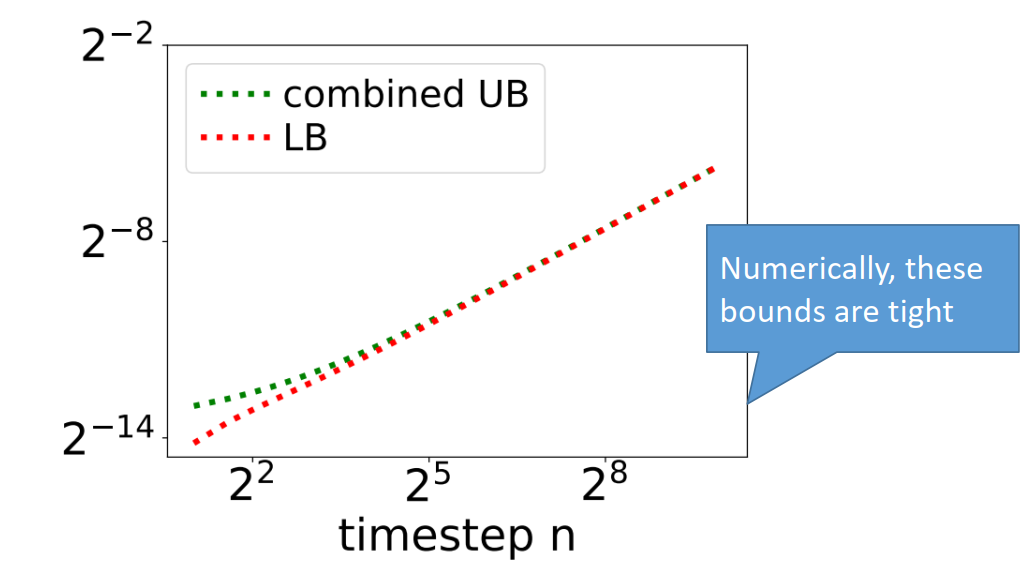
可以看到上下界都十分紧。

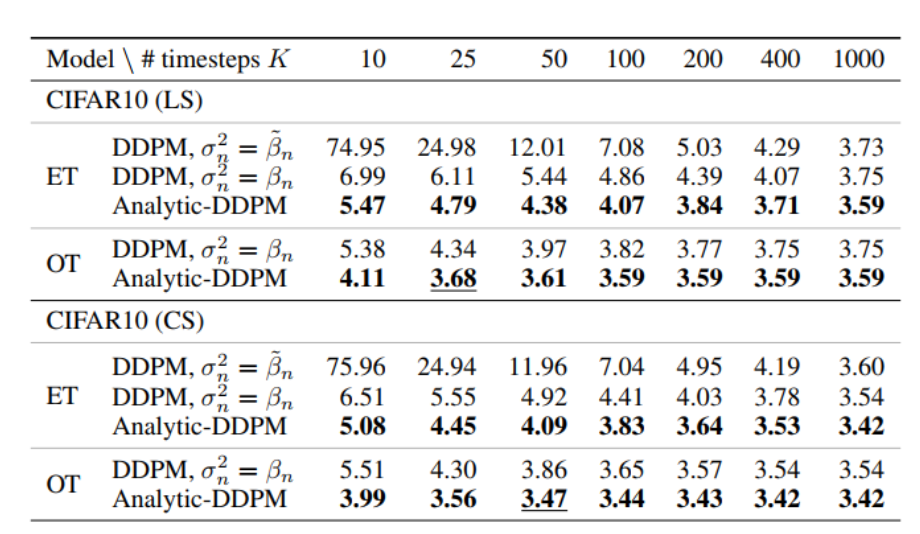
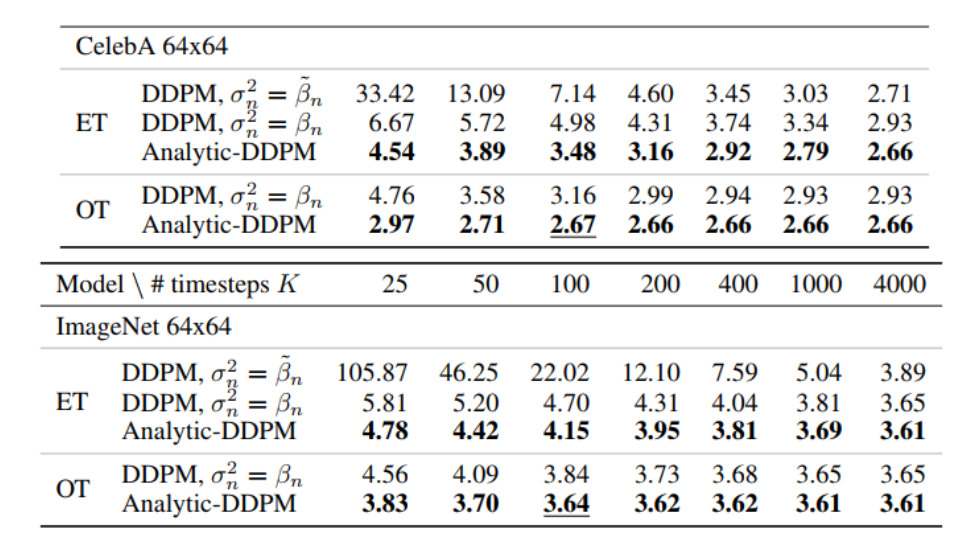
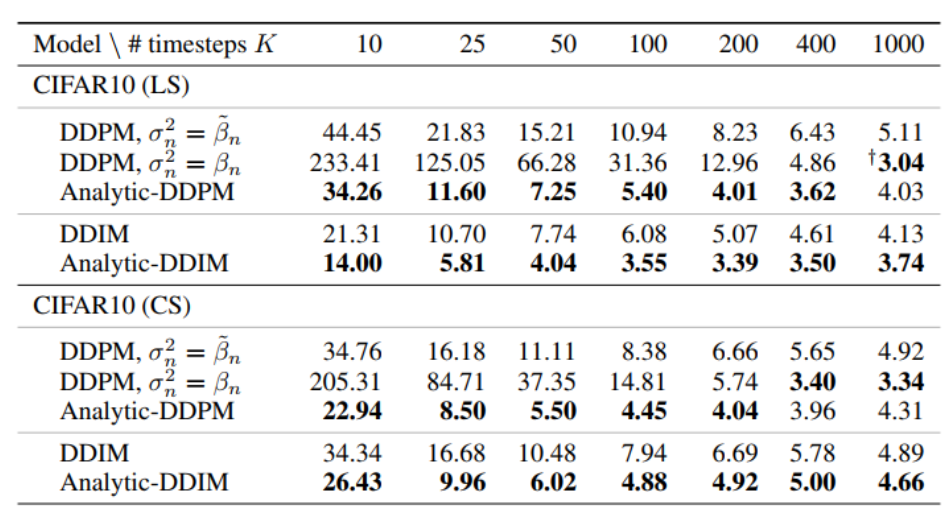
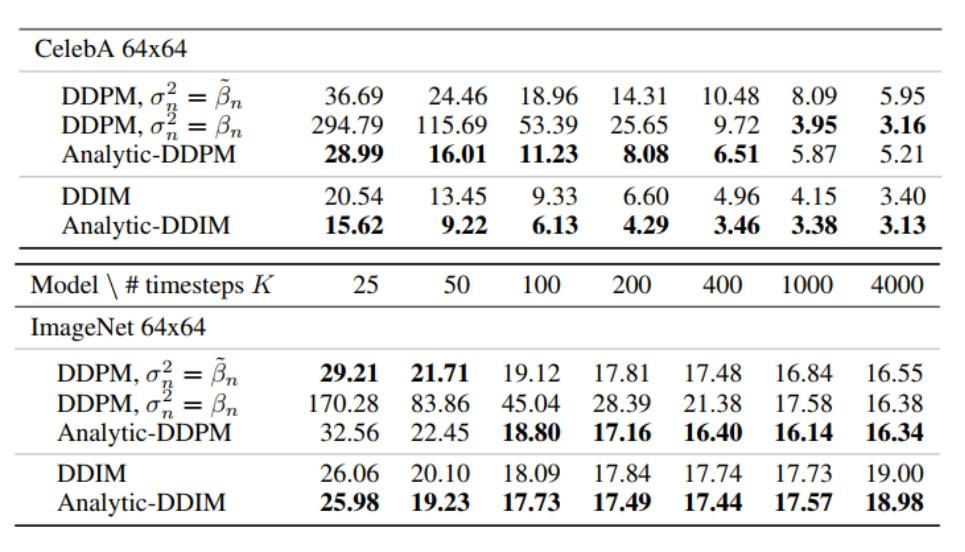
Analytic-DPM 速度和性能都完美超越 DDPM。

此外，对角协方差的解析解为： \[ \mu_n^*(x_n) = \frac{1}{\sqrt{\alpha_n}} \left( x_n - \frac{\beta_n}{\sqrt{\bar{\beta}_n}} \mathbf{E}_{q(x_0|x_n)}[\epsilon_n] \right) \]

\[ \sigma_n^*(x_n)^2 = \frac{\bar{\beta}_{n-1}}{\bar{\beta}_n} \beta_n + \frac{\beta_n^2}{\bar{\beta}_n \alpha_n} (\mathbb{E}_{q(x_0|x_n)}[\epsilon_n^2] - \mathbb{E}_{q(x_0|x_n)}[\epsilon_n]^2) \] 其中 \(\sigma^*_n\) 的第一个 \(\mathbb{E}\) 约等于 \(h_n(x_n)\)，第二个约等于 \(\hat{\epsilon}_n(x_n)^2\)，这里预测的是平方噪音 squared noise（SN） \(\epsilon_n^2\)。但实际中的 \(\hat{\epsilon}_n(x_n)\) 和 \(\mu_n(x_n)\) 都不是最佳的。为此，可以预测误差的期望： \[ \tilde{\sigma}_n^*(x_n)^2 = \frac{\bar{\beta}_{n-1}}{\bar{\beta}_n} \beta_n + \underbrace{\frac{\beta_n^2}{\bar{\beta}_n \alpha_n} \mathbf{E}_{q(x_0|x_n)} [(\epsilon_n - \hat{\epsilon}_n(x_n))^2]}_{\approx g_n(x_n)} . \]

\[ \min_{g_n} \mathbf{E}_{q(x_0, x_n)} \left\| h_n(x_n) - \boxed{(\epsilon_n - \hat{\epsilon}_n(x_n))^2} \right\|^2 \]

圈起来的也叫噪声预测残差 noise prediction residual （NPR）。

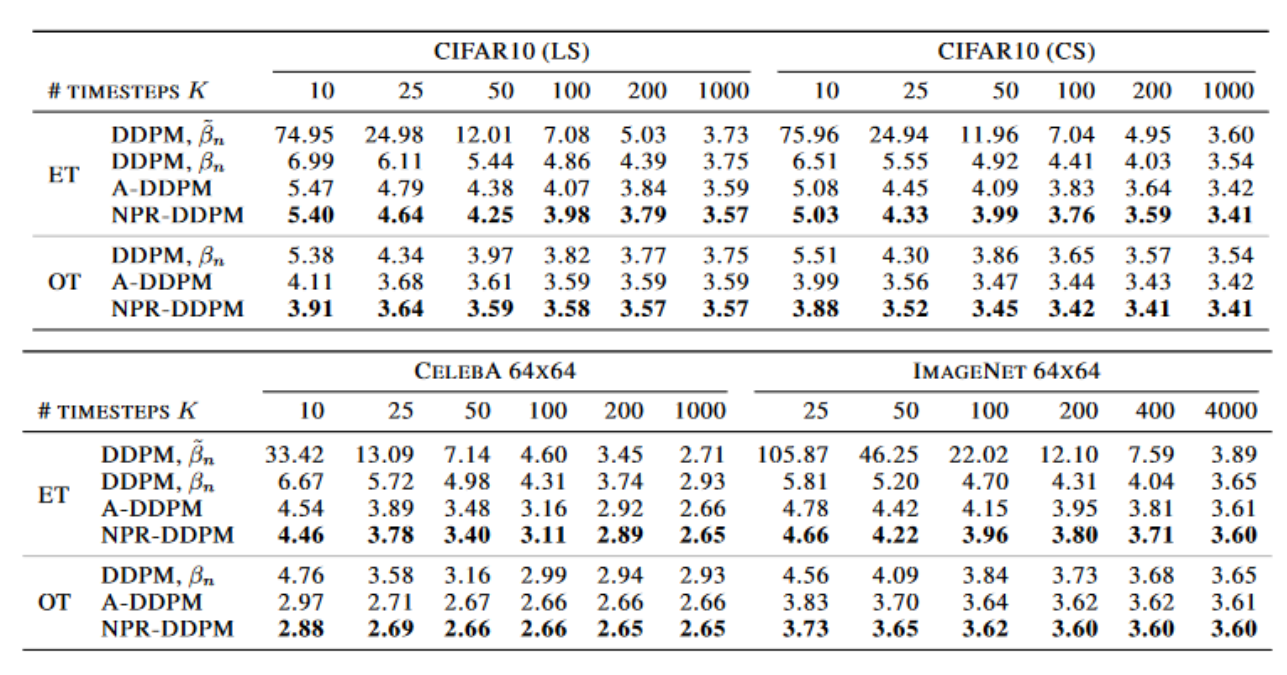
对于输出的似然，直接预测 NPR 效果也比 Analysic-DPM，A-DDPM 要好。

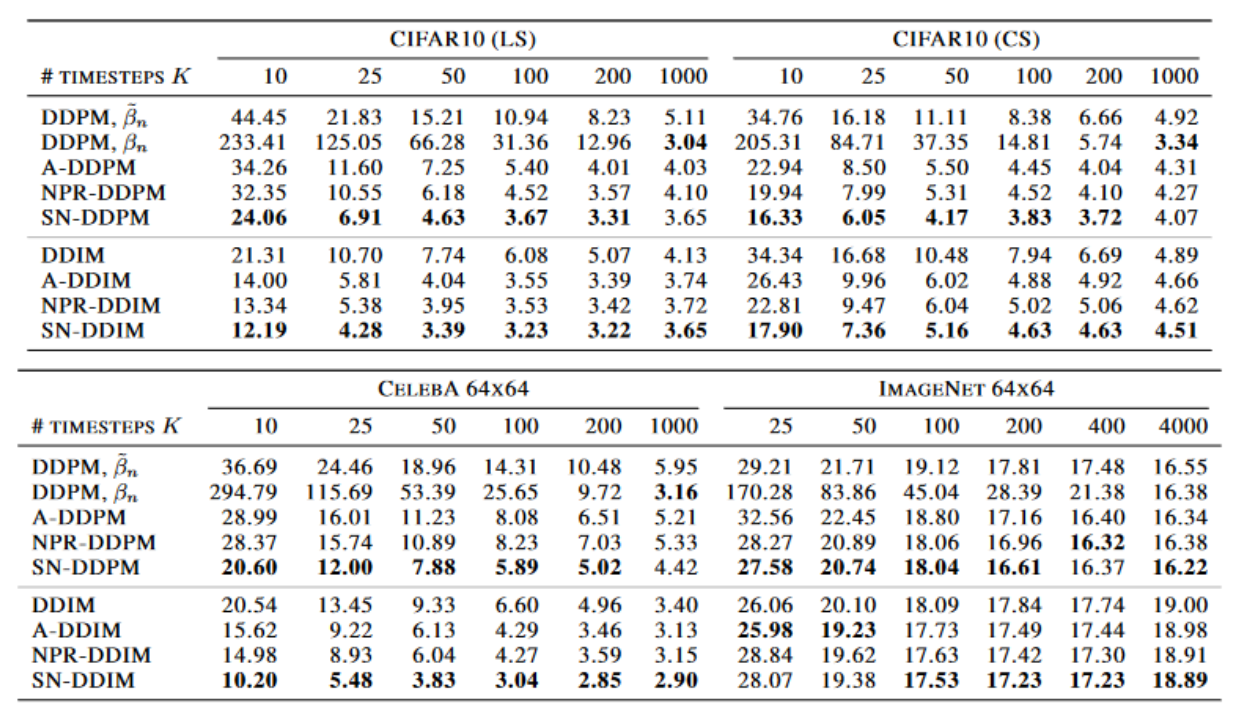
SN-DPM 和 NPR-DPM 的生成质量都比 Analytic-DPM 要好。

DPM-Solver：加速 ODE 求解

DPM-Solver 优化了 DDIM 中对 ODE 求解的方法。

正如之前提到的，扩散模型反向可以通过随机的 SDE（DDPM）： \[ \mathrm{d}\boldsymbol{x}_t = \left[ f(t)\boldsymbol{x}_t + \frac{g^2(t)}{\sigma_t}\boldsymbol{\epsilon}_\theta(\boldsymbol{x}_t, t) \right] \mathrm{d}t + g(t)\mathrm{d}\bar{\boldsymbol{w}}_t, \quad \boldsymbol{x}_T \sim \mathcal{N}(\mathbf{0}, \tilde{\sigma}^2 \boldsymbol{I}). \]

也可以通过确定的 ODE（DDIM）： \[ \frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t} = f(t)\boldsymbol{x}_t + \frac{g^2(t)}{2\sigma_t}\boldsymbol{\epsilon}_\theta(\boldsymbol{x}_t, t), \quad \boldsymbol{x}_T \sim \mathcal{N}(\mathbf{0}, \tilde{\sigma}^2 \boldsymbol{I}) \] 但 DPMs 最大的问题就是采样速度太慢（迭代次数过多），一般就算是 ODE 都需要 100 步才能收敛。

因为噪音变化不能太大，所以需要逐渐慢慢的加噪、去噪。

DPM-Solver 仅需要 10-20 步：

假设起始时间 \(s\) 的初始值为 \(x_s\)，那么时间 \(t\) 的解 \(x_t\) 满足了： \[ \boldsymbol{x}_t = \boldsymbol{x}_s + \int_{s}^{t} \underbrace{\left( f(\tau)\boldsymbol{x}_\tau + \frac{g^2(\tau)}{2\sigma_\tau} \boldsymbol{\epsilon}_\theta(\boldsymbol{x}_\tau, \tau) \right)}_{\text{A ``black-box'' } \quad \boldsymbol{h}_\theta(\boldsymbol{x}_t, t)} \mathrm{d}\tau \] 可以看到，解仅用到了一个黑盒函数 \(h_\theta(x_t,t)\)，没有用到已知信息 \(f(t), g(t)\)，那我们不如将此黑盒函数拆分，将线性部分提取出来直接计算，减轻负担。考虑： \[ \frac{\mathrm{d}\boldsymbol{x}_t}{\mathrm{d}t} = \boxed{f(t)\boldsymbol{x}_t} + \frac{g^2(t)}{2\sigma_t}\boldsymbol{\epsilon}_\theta(\boldsymbol{x}_t, t) \] 第一项是线性函数，于是通过 variation of constants 公式，第一项存在解析解： \[ \boldsymbol{x}_t = \boxed{e^{\int_{s}^{t} f(\tau)\mathrm{d}\tau} \boldsymbol{x}_s} + \int_{s}^{t} \left( e^{\int_{\tau}^{t} f(r)\mathrm{d}r} \frac{g^2(\tau)}{2\sigma_\tau} \boldsymbol{\epsilon}_\theta(\boldsymbol{x}_\tau, \tau) \right) \mathrm{d}\tau \] 第一项不需要考虑 DPM 的神经网络，可以直接计算，第二部分计算量减少了。这样，神经网络 \(\boldsymbol{\epsilon}_\theta\) 只需要负责预测纯粹的噪声方向，而不必去拟合那种由 \(f(t)\) 带来的确定性衰减规律。

通过还原可以简化上述表达。考虑信噪比（signal to noise ratio，SNR）\(\alpha_t^2/\sigma_t^2\)，定义 \(\lambda_t:=\log(\alpha_t/\sigma_t)\)，可以证明： \[ f(t) = \frac{\text{t} \log \alpha_t}{\text{d} t}\\ g^2(t)=-2\sigma^2_t\frac{\text{d}\lambda_t}{\text{d}t} \] 于是，简化原式为： \[ \boldsymbol{x}_t = \underbrace{\frac{\alpha_t}{\alpha_s} \boldsymbol{x}_s}_{\substack{\text{Linear term} \\ \text{Exactly Computed}}} - \alpha_t \underbrace{\int_{\lambda_s}^{\lambda_t} e^{-\lambda} \hat{\boldsymbol{\epsilon}}_\theta(\hat{\boldsymbol{x}}_\lambda, \lambda) \mathrm{d}\lambda}_{\substack{\text{Nonlinear term} \\ \text{Exponentially weighted integral}}} \] 其中非线性积分可以通过高阶近似来解。

给定时间 \(t_{i-1}\) 的 \(\tilde{x}_{t_{i-1}}\)，\(t_{i}\) 时的解为： \[ \boldsymbol{x}_{t_{i-1} \to t_i} = \frac{\alpha_{t_i}}{\alpha_{t_{i-1}}} \tilde{\boldsymbol{x}}_{t_{i-1}} - \alpha_{t_i} \int_{\lambda_{t_{i-1}}}^{\lambda_{t_i}} e^{-\lambda} \hat{\boldsymbol{\epsilon}}_\theta(\hat{\boldsymbol{x}}_\lambda, \lambda) \mathrm{d}\lambda \] 泰勒展开 \(\hat{\epsilon}_\theta\)： \[ \hat{\boldsymbol{\epsilon}}_\theta(\hat{\boldsymbol{x}}_\lambda, \lambda) = \sum_{n=0}^{k-1} \frac{(\lambda - \lambda_{t_{i-1}})^n}{n!} \hat{\boldsymbol{\epsilon}}_\theta^{(n)}(\hat{\boldsymbol{x}}_{\lambda_{t_{i-1}}}, \lambda_{t_{i-1}}) + \mathcal{O}((\lambda - \lambda_{t_{i-1}})^k) \] 得到： \[ \boldsymbol{x}_{t_{i-1} \to t_i} = \frac{\alpha_{t_i}}{\alpha_{t_{i-1}}} \tilde{\boldsymbol{x}}_{t_{i-1}} - \alpha_{t_i} \sum_{n=0}^{k-1} \underbrace{\hat{\boldsymbol{\epsilon}}_\theta^{(n)}(\hat{\boldsymbol{x}}_{\lambda_{t_{i-1}}}, \lambda_{t_{i-1}})}_{\text{Derivatives}} \underbrace{\int_{\lambda_{t_{i-1}}}^{\lambda_{t_i}} e^{-\lambda} \frac{(\lambda - \lambda_{t_{i-1}})^n}{n!} \mathrm{d}\lambda}_{\text{Coefficients}} + \mathcal{O}(h_i^{k+1}) \] 更进一步，因为 \(\lambda\) 的换元，我们可以通过 \(n\) 次分部积分来得到系数 Coefficients 的精确解： \[ \begin{aligned} \int_{\lambda_{t_{i-1}}}^{\lambda_{t_i}} e^{-\lambda} \frac{(\lambda - \lambda_{t_{i-1}})^n}{n!} \mathrm{d}\lambda &= - \int_{\lambda_{t_{i-1}}}^{\lambda_{t_i}} \frac{(\lambda - \lambda_{t_{i-1}})^n}{n!} \mathrm{d}(e^{-\lambda}) \\ &= \left( - \frac{(\lambda - \lambda_{t_{i-1}})^n}{n!} e^{-\lambda} \right) \bigg|_{\lambda_{t_{i-1}}}^{\lambda_{t_i}} + \int_{\lambda_{t_{i-1}}}^{\lambda_{t_i}} e^{-\lambda} \frac{(\lambda - \lambda_{t_{i-1}})^{n-1}}{(n - 1)!} \mathrm{d}\lambda \\ &= \dots \end{aligned} \] 而导数 Derivatives 的部分，高阶 ODE 求解器（如 RK4 等）通常涉及复杂的导数计算。如果在推理阶段使用深度学习框架的自动微分（Autograd）来算 U-Net 的高阶导数，计算量将巨大且速度极慢。为了避免自动微分 Autograd，可以通过计算神经网络在当前点 \(\lambda_{t_{i-1}}\) 和某个中间点（或前一个点）\(s_i\) 的函数值之差，来估算其导数。 \[ \hat{\epsilon}_\theta^{(1)}(\hat{\mathbf{x}}_{\lambda_{t_{i-1}}}, \lambda_{t_{i-1}}) \approx \frac{\hat{\epsilon}_\theta(\hat{\mathbf{x}}_{s_i}, s_i) - \hat{\epsilon}_\theta(\hat{\mathbf{x}}_{\lambda_{t_{i-1}}}, \lambda_{t_{i-1}})}{s_i - \lambda_{t_{i-1}}} \] 这种方法只需要对神经网络进行前向求值（Function evaluation），完全不需要运行 Autograd，从而保持了计算的高效性。

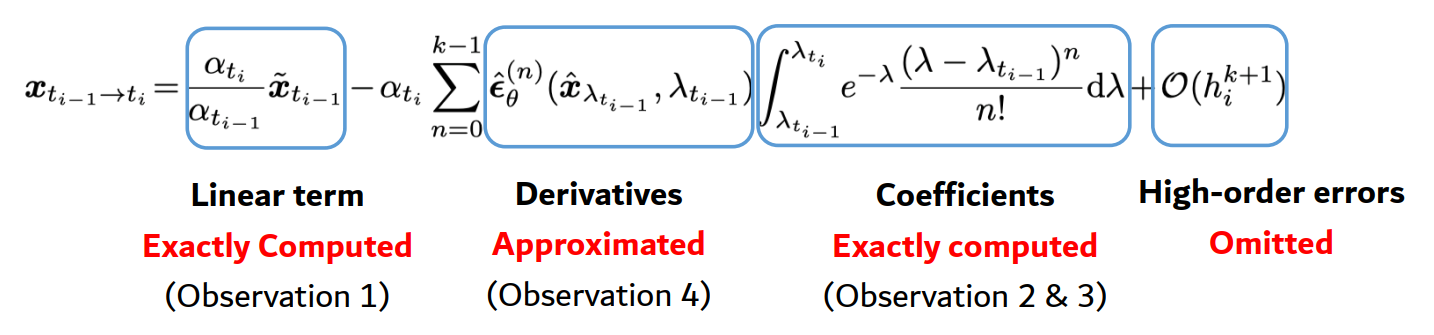
于是，DPM-Solver 通过上述方法，对涉及神经网络的项进行近似，对其他项获取精确解，并省略高阶误差，显著的降低了计算量和增快了迭代速度。

DDIM 是一阶 DPM-Solver

对 \(k=2\) 的特例，可以看到： \[ \begin{aligned} \boldsymbol{x}_{t_{i-1} \to t_i} &= \frac{\alpha_{t_i}}{\alpha_{t_{i-1}}} \tilde{\boldsymbol{x}}_{t_{i-1}} - \alpha_{t_i} \boldsymbol{\epsilon}_\theta(\tilde{\boldsymbol{x}}_{t_{i-1}}, t_{i-1}) \int_{\lambda_{t_{i-1}}}^{\lambda_{t_i}} e^{-\lambda} \mathrm{d}\lambda + \mathcal{O}(h_i^2) \\ &= \frac{\alpha_{t_i}}{\alpha_{t_{i-1}}} \tilde{\boldsymbol{x}}_{t_{i-1}} - \sigma_{t_i} (e^{h_i} - 1) \boldsymbol{\epsilon}_\theta(\tilde{\boldsymbol{x}}_{t_{i-1}}, t_{i-1}) + \mathcal{O}(h_i^2). \end{aligned} \]

而这完全对应了 DDIM。所以可以看到 DDIM 就是精确计算出所有项的一阶扩散 ODE Solver。

通过引入更高阶，可以在大幅减少采样步数（提升速度）的同时，通过降低数学上的离散化误差，保持甚至提升生成图像的质量。

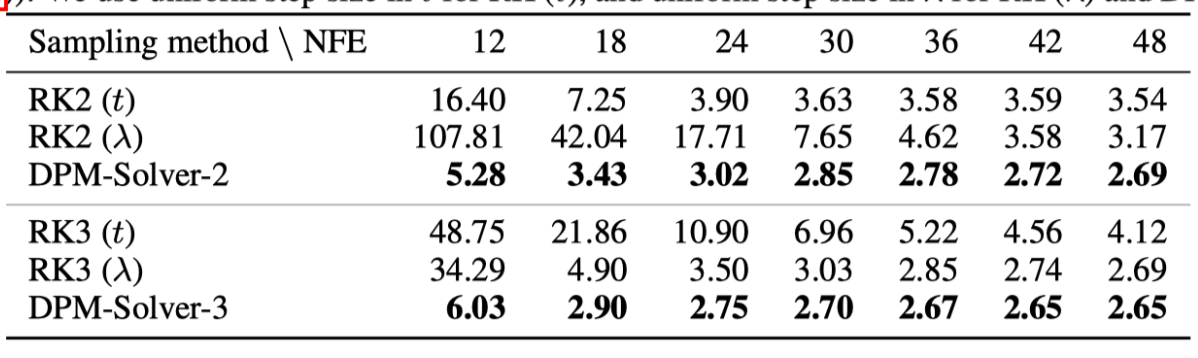
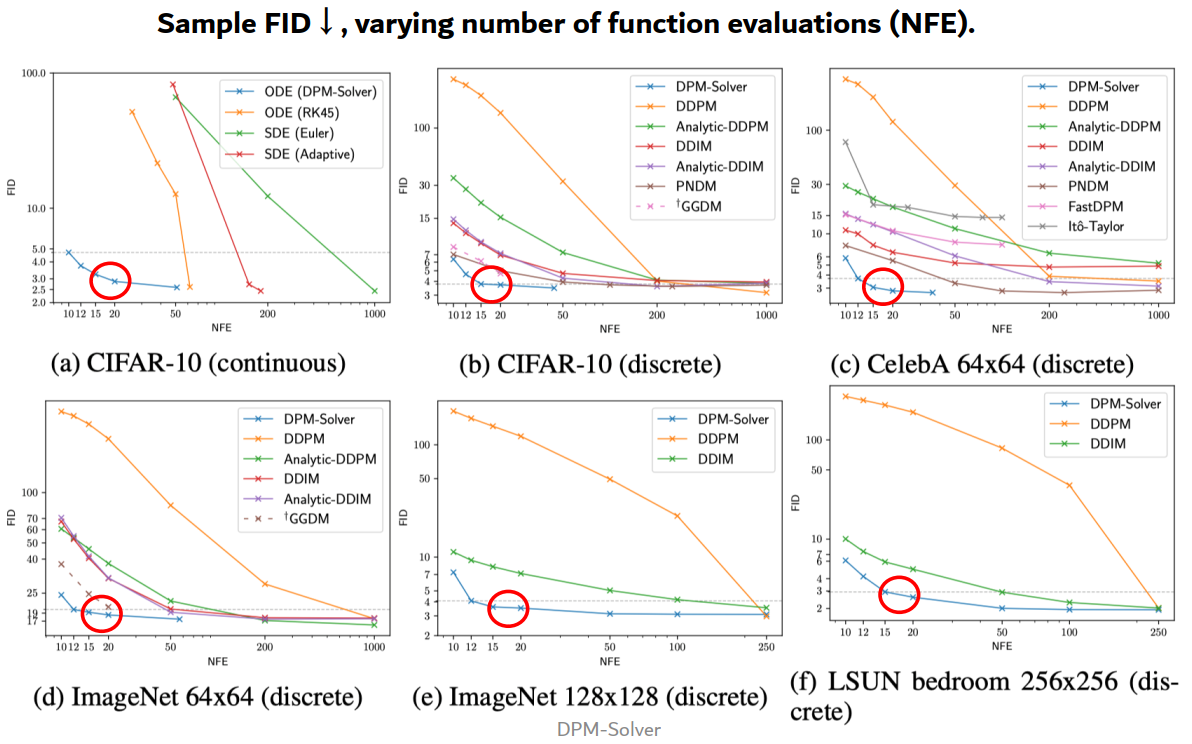
DPM-Solver++

为了控制生成内容，我们需要对模型进行“引导”（仅需要修改噪音预测模型）。

分类器引导 (Classifier Guidance)：利用一个额外的分类器的梯度 \(\nabla_{\mathbf{x}_t} \log p_\phi(c|\mathbf{x}_t, t)\) 来修正噪声预测值： \[ \tilde{\boldsymbol{\epsilon}}_\theta(\boldsymbol{x}_t, t, c) := \boldsymbol{\epsilon}_\theta(\boldsymbol{x}_t, t) - \boxed{s} \cdot \sigma_t \underbrace{\nabla_{\boldsymbol{x}_t} \log p_\phi(c|\boldsymbol{x}_t, t)}_{\text{Classifier}} \] 无分类器引导 (Classifier-free guidance, CFG)：通过线性组合有条件模型 \(\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, c)\) 和无条件模型 \(\boldsymbol{\epsilon}_\theta(\mathbf{x}_t, t, \emptyset)\) 来引导： \[ \tilde{\boldsymbol{\epsilon}}_\theta(\boldsymbol{x}_t, t, c) := \boxed{s} \cdot \boldsymbol{\epsilon}_\theta(\boldsymbol{x}_t, t, c) + (1 - s) \cdot \underbrace{\boldsymbol{\epsilon}_\theta(\boldsymbol{x}_t, t, \varnothing)}_{\text{Unconditional model}} \] 这里的引导尺度 \(s\) 一般较大。增大 \(s\) 通常会提高生成结果与条件的匹配度，但可能会降低样本的多样性。

但存在两个问题：

• 训练-测试不匹配：当引导缩放因子 \(s\) 很大时，预测值会超出图像正常的范围 \([0, 255]\)，导致生成图像颜色扭曲或饱和度过高。

• 高阶解算器不稳定：在 \(s\) 较大时，普通的高阶求解器（如 PNDM 或原版 DPM-Solver 3阶）会出现严重的伪影或完全崩溃。

这里 \(s=8.0\)。

从 DPM-Solver 到 DPM-Solver++

原版 DPM-Solver 预测的是噪声 \(\boldsymbol{\epsilon}\)，而 DPM-Solver++ 预测的是原始数据（即 \(x_0\)）的估计值： \[ \boldsymbol{x}_\theta(\boldsymbol{x}_t, t) := (\boldsymbol{x}_t - \sigma_t \boldsymbol{\epsilon}_\theta(\boldsymbol{x}_t, t))/\alpha_t \] 对于解： \[ \boldsymbol{x}_{t_{i-1} \to t_i} = \frac{\sigma_{t_i}}{\sigma_{t_{i-1}}} \tilde{\boldsymbol{x}}_{t_{i-1}} + \sigma_{t_i} \int_{\lambda_{t_{i-1}}}^{\lambda_{t_i}} e^\lambda \hat{\boldsymbol{x}}_\theta(\hat{\boldsymbol{x}}_\lambda, \lambda) \mathrm{d}\lambda \] 通过泰勒展开可以变为： \[ \tilde{\boldsymbol{x}}_{t_i} = \frac{\sigma_{t_i}}{\sigma_{t_{i-1}}} \tilde{\boldsymbol{x}}_{t_{i-1}} + \sigma_{t_i} \sum_{n=0}^{k-1} \underbrace{\boldsymbol{x}_\theta^{(n)}(\hat{\boldsymbol{x}}_{\lambda_{t_{i-1}}}, \lambda_{t_{i-1}})}_{\text{estimated}} \underbrace{\int_{\lambda_{t_{i-1}}}^{\lambda_{t_i}} e^\lambda \frac{(\lambda - \lambda_{t_{i-1}})^n}{n!} \mathrm{d}\lambda}_{\text{analytically computed (Appendix A)}} + \underbrace{\mathcal{O}(h_i^{k+1})}_{\text{omitted}} \]

单步 (2S) 与 多步 (2M) 求解器：

• 2S (Singlestep)：每一步需要多次函数调用（NFE），计算较重。
• 2M (Multistep)：利用一个缓冲区 \(Q\) 存储之前的模型输出。这使得它可以用和 DDIM 一样少的函数调用次数（每步仅 1 次 NFE），却能达到高阶精度。

一致性模型蒸馏 (Consistency Distillation, CD)

这是目前非常主流且高效的方法，由 OpenAI 的宋飏等人提出。

• 核心理念：引入一致性函数（Consistency Function）。该函数可以将扩散过程 ODE 轨迹上的任何点，直接映射到轨迹的终点（即原始图像 \(x_0\)）。
• 逻辑：无论你在去噪过程的哪个阶段（哪个时间步），模型预测出的结果都应该指向同一个终点。
• 成果：能够实现真正的 1 步生成（Single-step generation），典型的应用包括 LCM (Latent Consistency Models)，它可以让 Stable Diffusion 在 4 步内出图。

特性	原始扩散模型 (Teacher)	蒸馏后的模型 (Student)
采样步数	20 - 100 步	1 - 8 步
推理速度	慢（数秒/张）	极快（毫秒级，可实时）
图像质量	高（细节丰富、多样性好）	较高（极低步数下可能有轻微细节损失）
训练成本	极高	较高（需要微调或重新训练）
计算资源	显存与算力开销大	显著降低采样阶段的开销

U-ViT：用 ViT 取代 U-Net

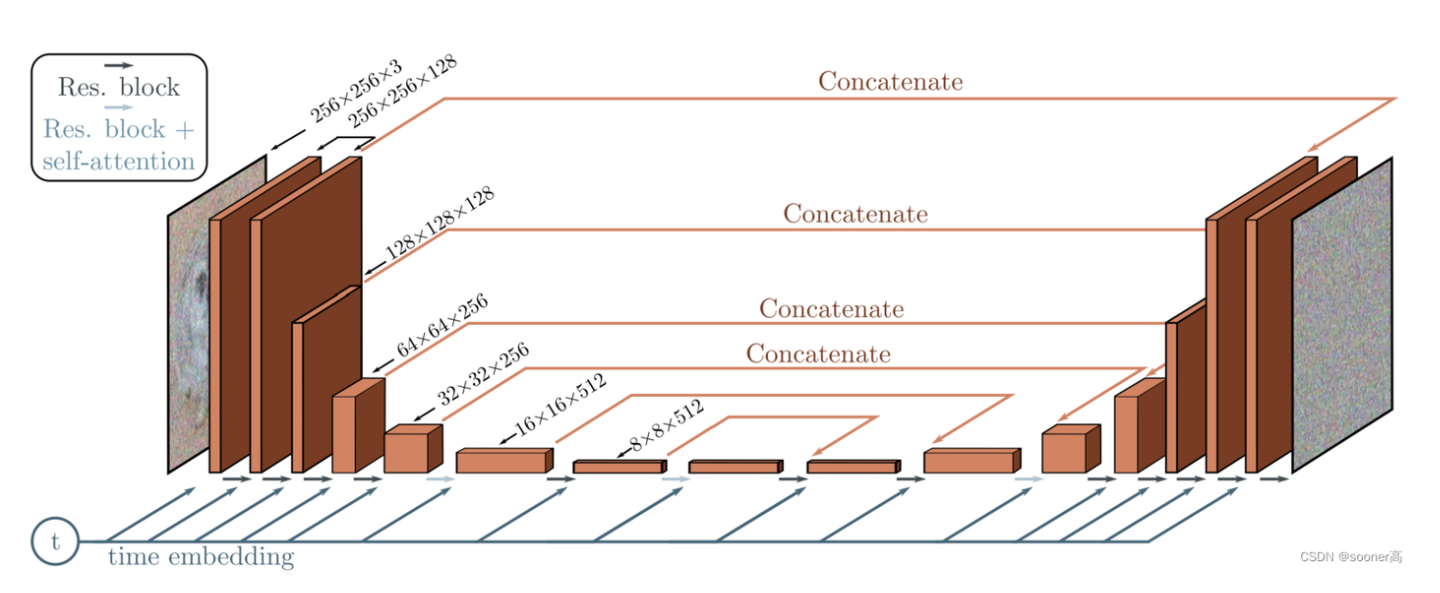
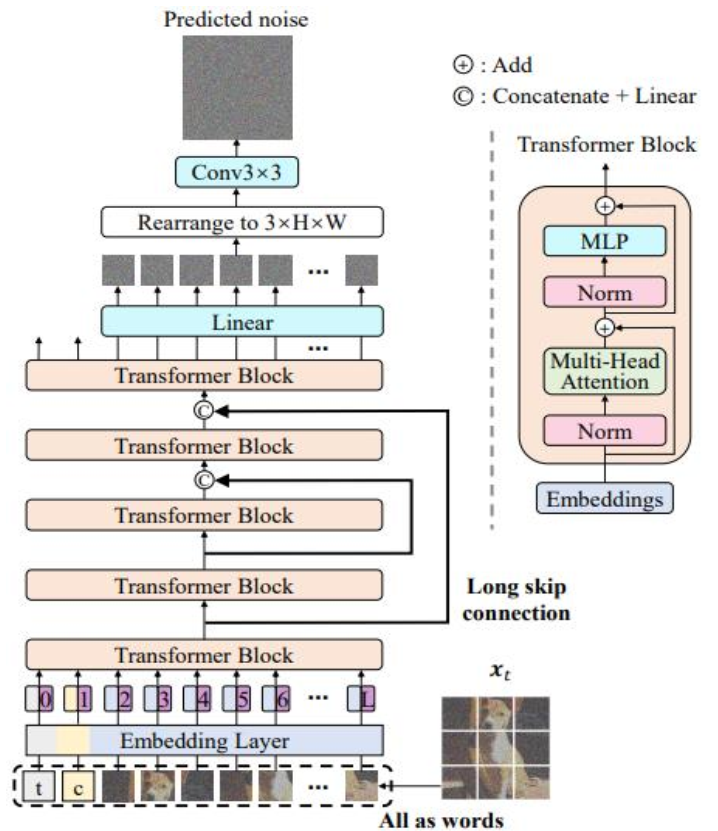
Vision Transformer（ViT）慢慢开始取代传统 CNN 模型（如 U-Net），扩散模型也一样。

传统的扩散模型用的都是基于 CNN 的 U-Net 架构，U-ViT 通过几个改进替换了 U-Net：

• 时间、条件、噪音图 patch 都为 tokens
• Long skip connection 【像 U-Net 一样在浅层和深层之间加长跳跃连接 (Long Skip Connection) 对生成低级特征（像素细节）至关重要。】
• 除了最后一层全是 Transformer

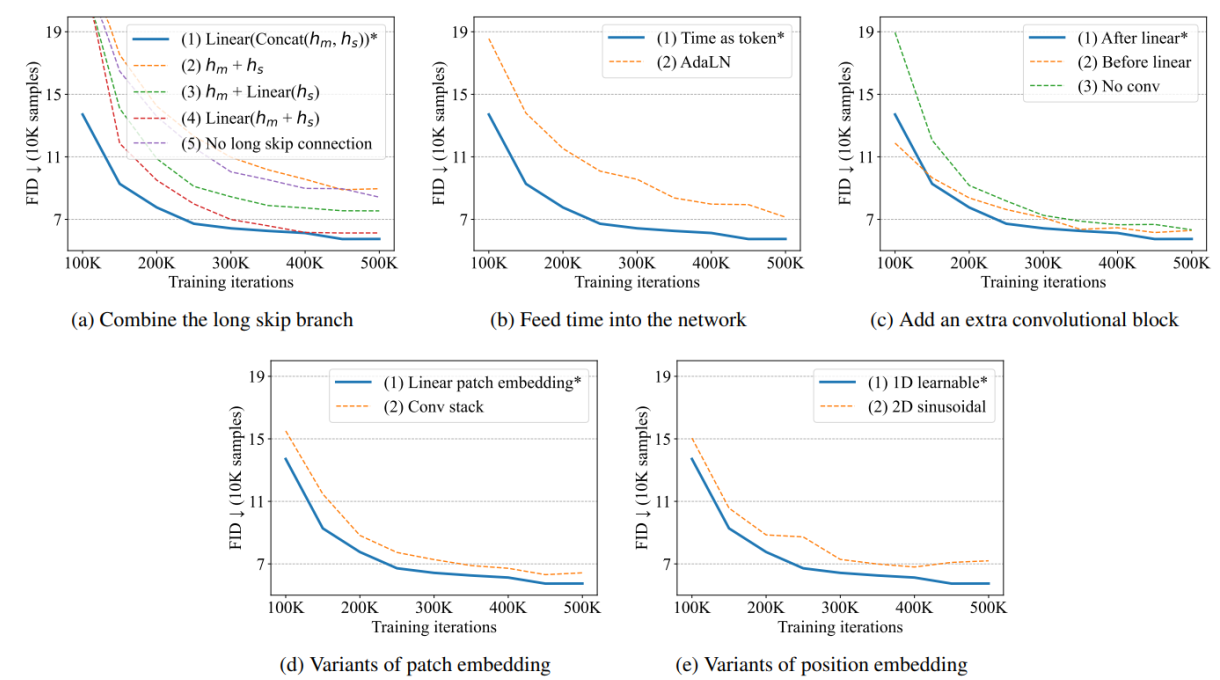
U-ViT 的可扩展性也不错：

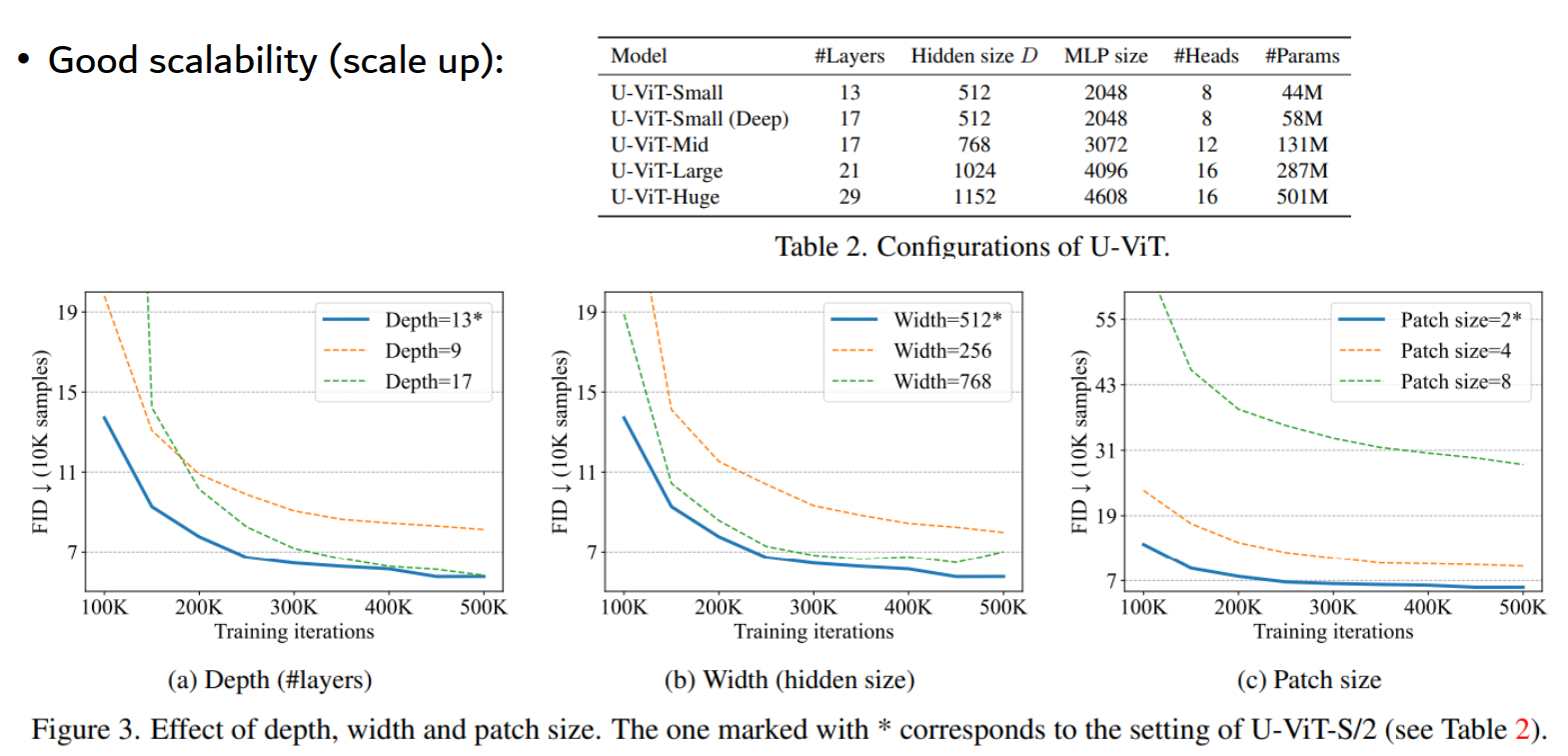
FID 指标也是 SOTA：

Diffusion Transformer：DiT

在生成模型（尤其是扩散模型）的演进中，U-ViT 和 DiT (Diffusion Transformer) 是将传统的 U-Net 替换为 Transformer 的两大标志性方案。

它们的核心目标一致：利用 Transformer 的可扩展性（Scaling Law）*和*全局注意力，打破 U-Net 在处理高分辨率、复杂跨模态任务时的性能瓶颈。

---

1. 要点概括

• DiT (Diffusion Transformer): 现代扩散模型的“标准间”。采用纯粹的直筒型（Straight-through）ViT 结构，通过自适应层归一化 (adaLN-Zero) 注入时间步和类别信息。是 Sora、Stable Diffusion 3 和 Flux.1 的技术底座。
• U-ViT: 融合了 U-Net 的灵魂与 Transformer 的躯干。它在 Transformer 层之间引入了类似 U-Net 的长距离跳跃连接 (Long Skip Connections)，并提出“All-in-One”思想，将所有信息（噪声图、时间、文本）全部 Token 化。

---

2. DiT (Diffusion Transformer)

由 William Peebles 和谢赛宁（谢赛宁也是 ResNeXt 和卷积神经网络 scaling 研究的领军人物）提出。

• 架构逻辑： 它是极其标准、模块化的 ViT。将图像划分为 Patches，然后送入一系列 Transformer Blocks。

• 核心创新：adaLN-Zero。

  这是 DiT 能训练成功的关键。它不是简单的 Cross-Attention，而是通过学习一个以时间步 \(t\) 和类别 \(c\) 为条件的缩放因子 (\(\gamma, \beta\)) 和门控值 (\(\alpha\))，直接作用于 Layer Norm 之后。

• 优势： 极强的可扩展性 (Scalability)。论文证明了随着模型规模（GFLOPs）的增加，生成质量（FID）呈现稳定的线性提升。这为后来的视频大模型提供了理论支撑。

---

3. U-ViT (All-in-One Transformer)

由清华大学朱军团队提出，旨在证明 Transformer 同样可以拥有 U-Net 的多尺度特征融合能力。

• 架构逻辑： 采用了类似 U-Net 的“对称”设计。
  • 跳跃连接： 将浅层编码器的输出与深层解码器的输入进行 Concatenate (拼接)，然后通过一个线性层降维。
  • All-in-One： 不再像传统模型那样分层注入信息，而是把 Time Embedding、Condition Embedding 也当做 Token，直接拼在图像 Token 序列的头部。
• 核心观察： 论文发现，在扩散模型中，Transformer 的深层和浅层之间共享特征（即跳跃连接）对于加速收敛和提升细节至关重要，尤其是在像素空间（Pixel Space）生成时。

---

4. U-ViT 与 DiT 的深度对比

特性	DiT (主流方案)	U-ViT (混合方案)
整体结构	直筒型 (Isotropic/Straight)	U-型 (带有长距离跳跃连接)
跳跃连接	无 (仅依靠深层堆叠)	有 (低层与高层特征融合)
条件注入	adaLN-Zero (调制 LN 参数)	Token-based (把条件当作普通 Token)
设计哲学	追求极致的 Scaling 和简洁	追求保留 U-Net 验证有效的感官偏置
代表应用	Sora, SD3, Flux, PixArt-\(\alpha\)	各种科研验证及特定学术任务

UniDiffuser：统一多模态生成

传统的模型大多数都是单向生成，如 Text-to-Image，如果想要反过来 Image-To-Text 那么需要重新训练一个模型。

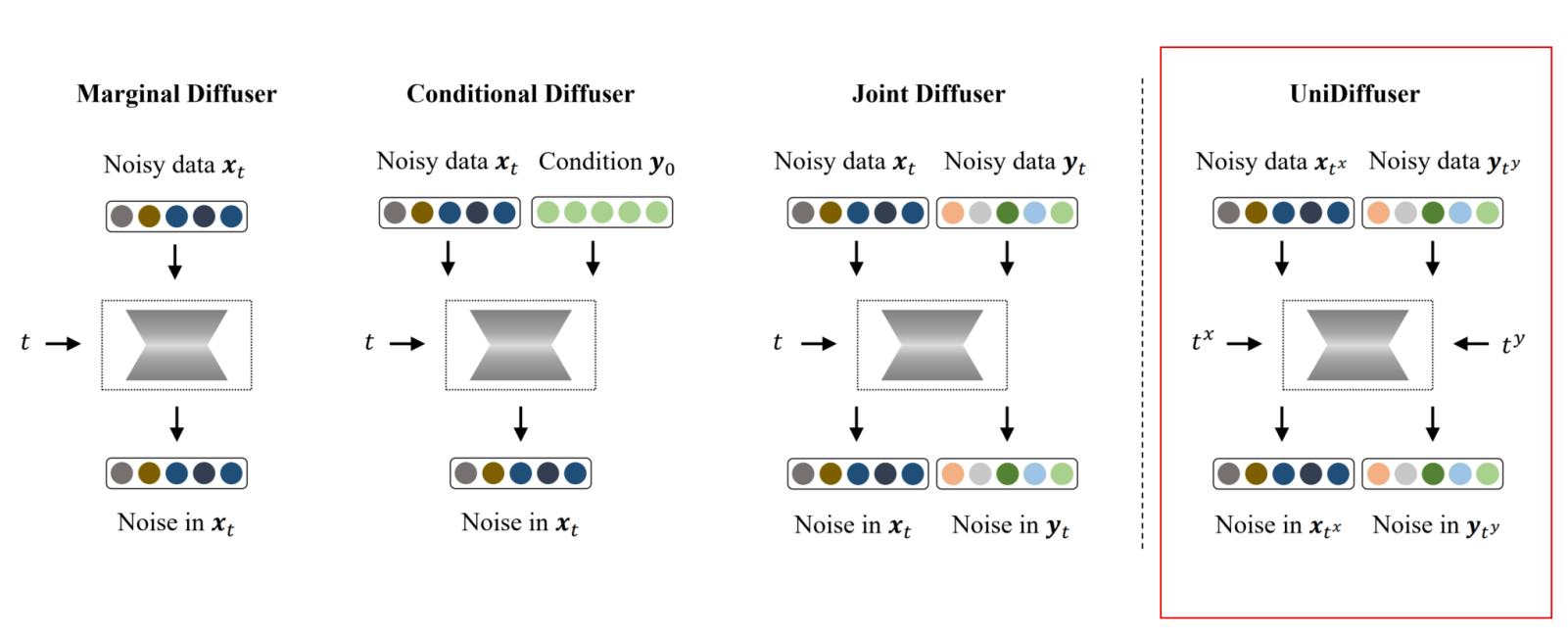
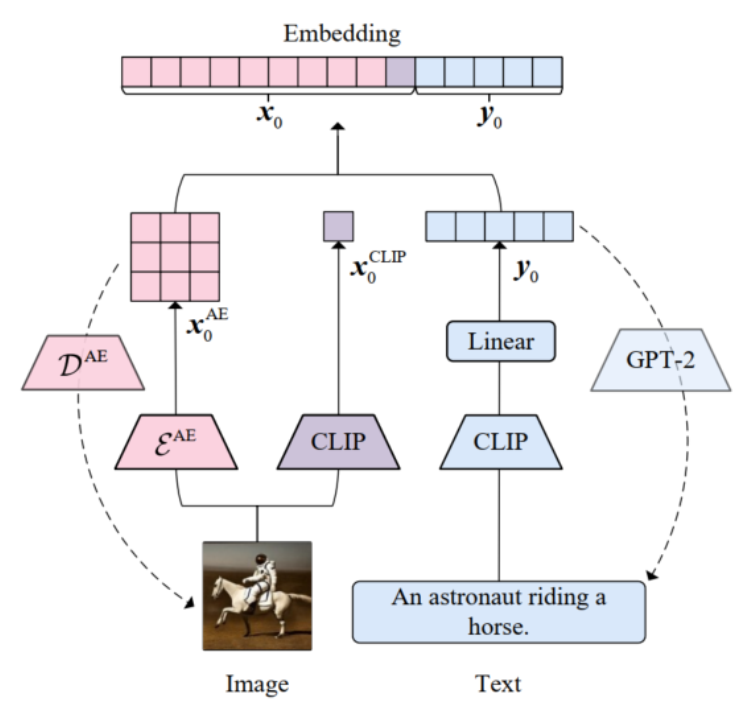
对于连续的图像和离散的文字，UniDiffuser 通过 VAE 压缩图像，和 CLIP 压缩文本，将特征拼接在一起，然后对所有特征同时添加噪声进行扰动并同时预测去噪结果。

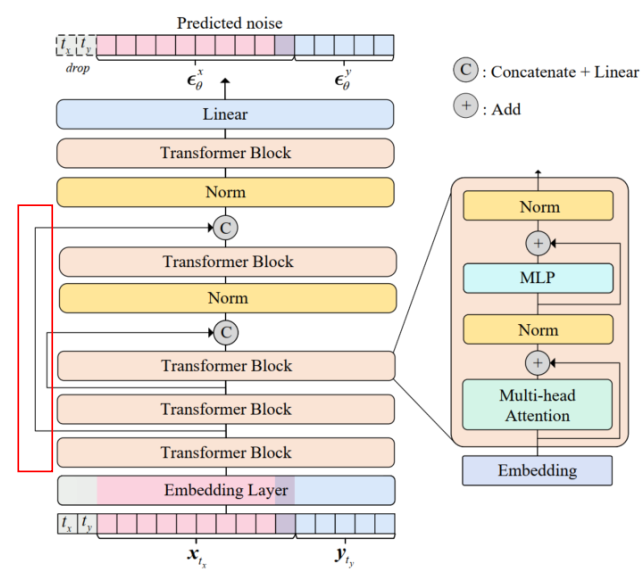
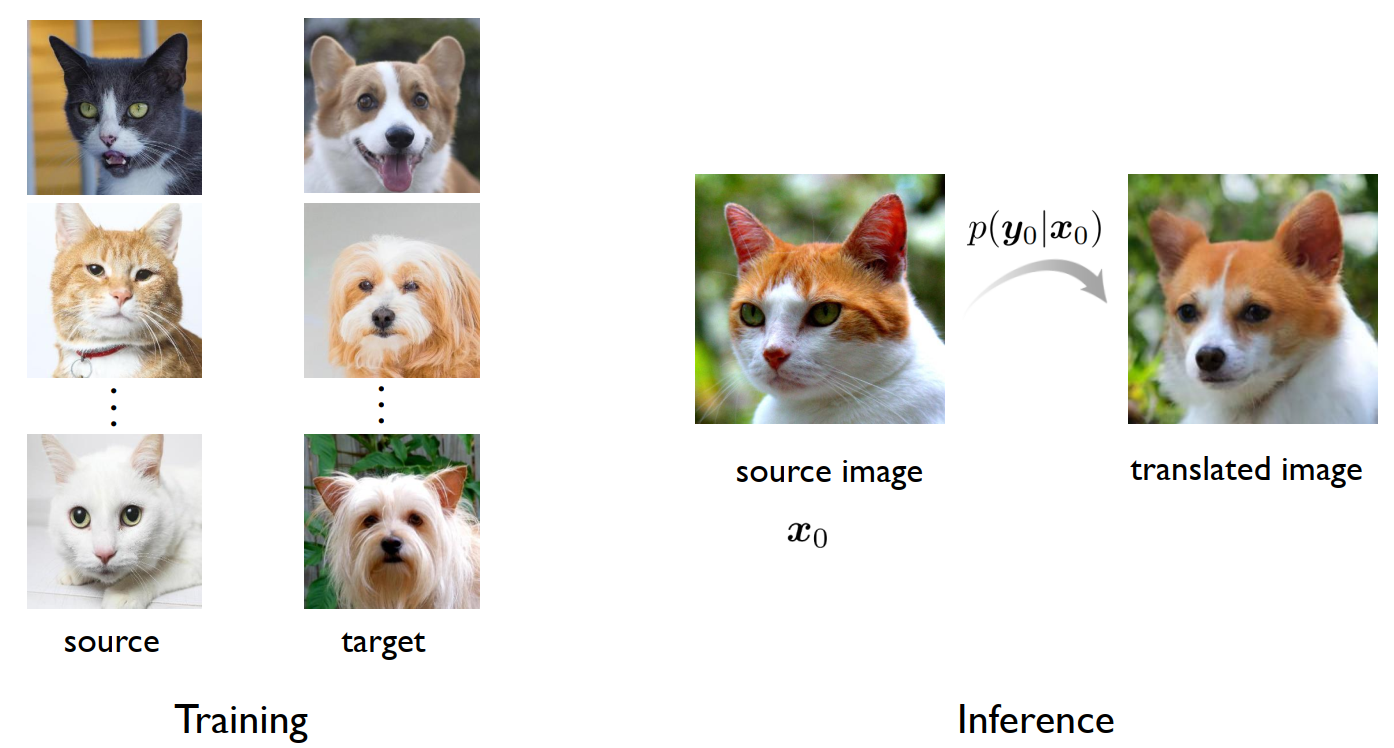
Energy-Guided Stochastic Differential Equations（EGSDE）：基于能量的图像翻译

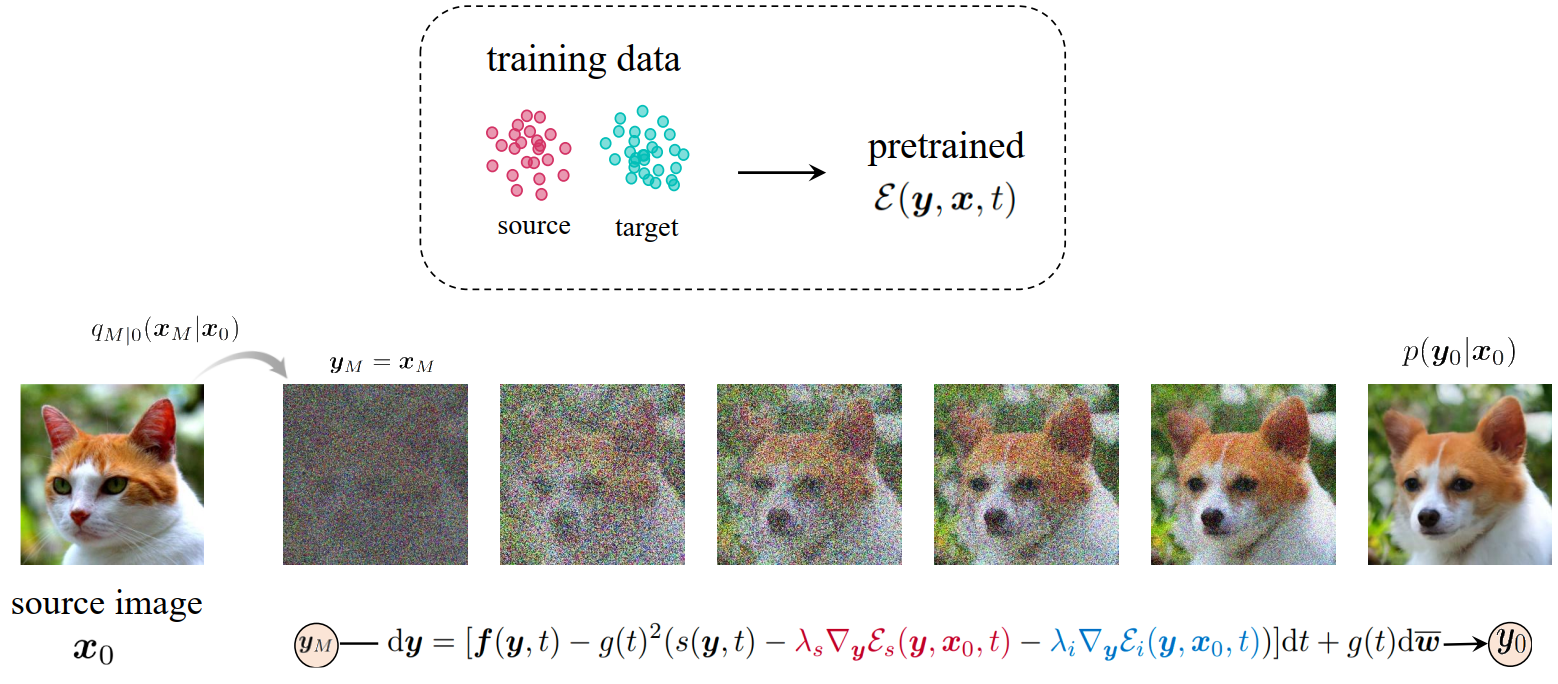
ProlificDreamer：Text-to-3D

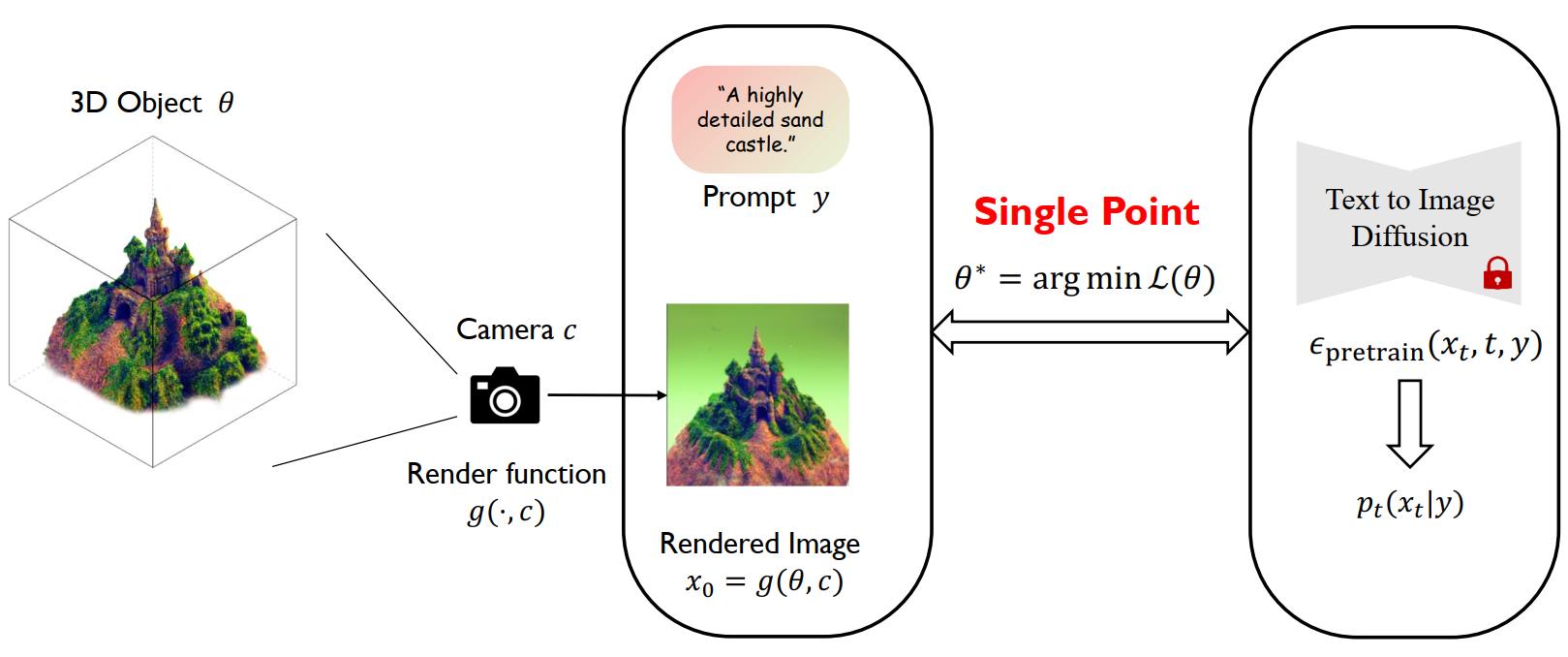
文字转 3D 最大的问题是没有像文本的大规模 3D 数据集。

Score Distillation Sampling（SDS）/ Score Jacobian Chaining（SJC）

SDS / SJC 将整个 3D 物品当作一个点来优化。更具体的，这让神经辐射场 NeRF 渲染出的 2D 图片，在扩散模型看来是“真实”的。

但从上面图片可以看到，SDS 生成的 3D 物体通常饱和度过高、平滑、细节丢失（Janus 问题）。

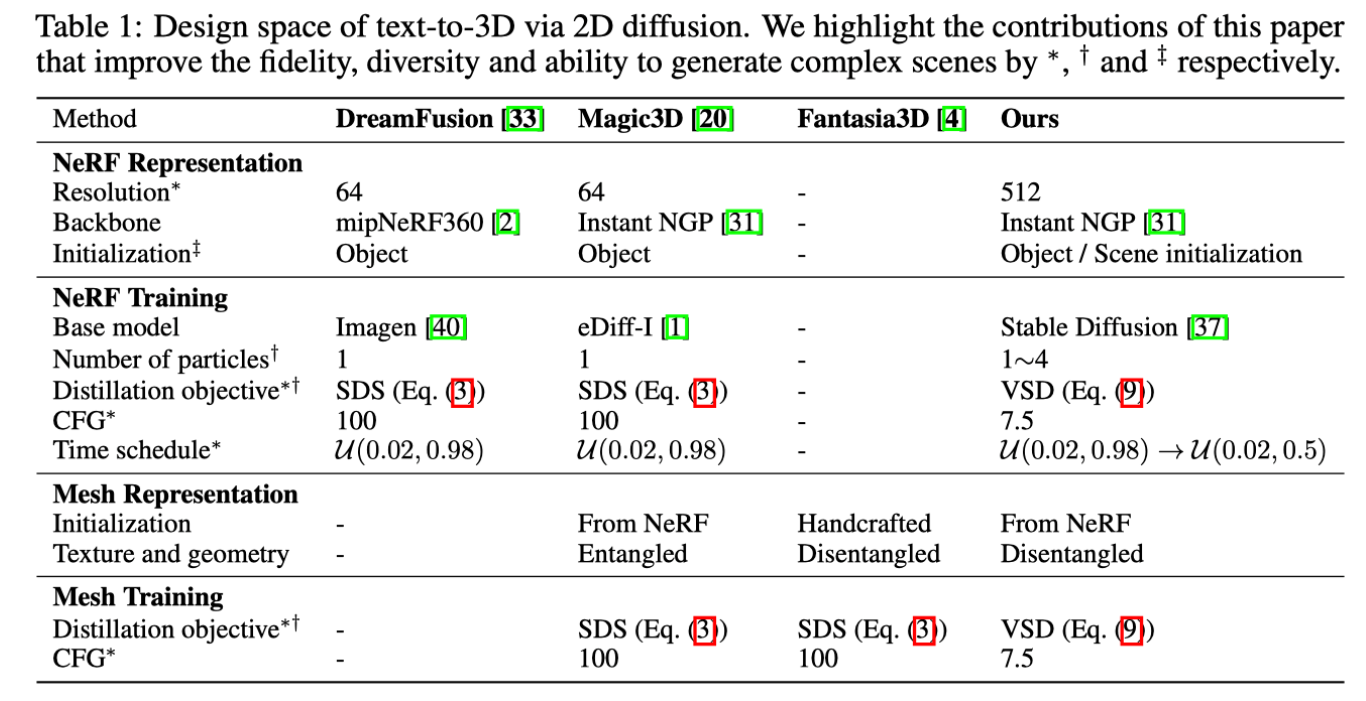
VSD (Variational Score Distillation)

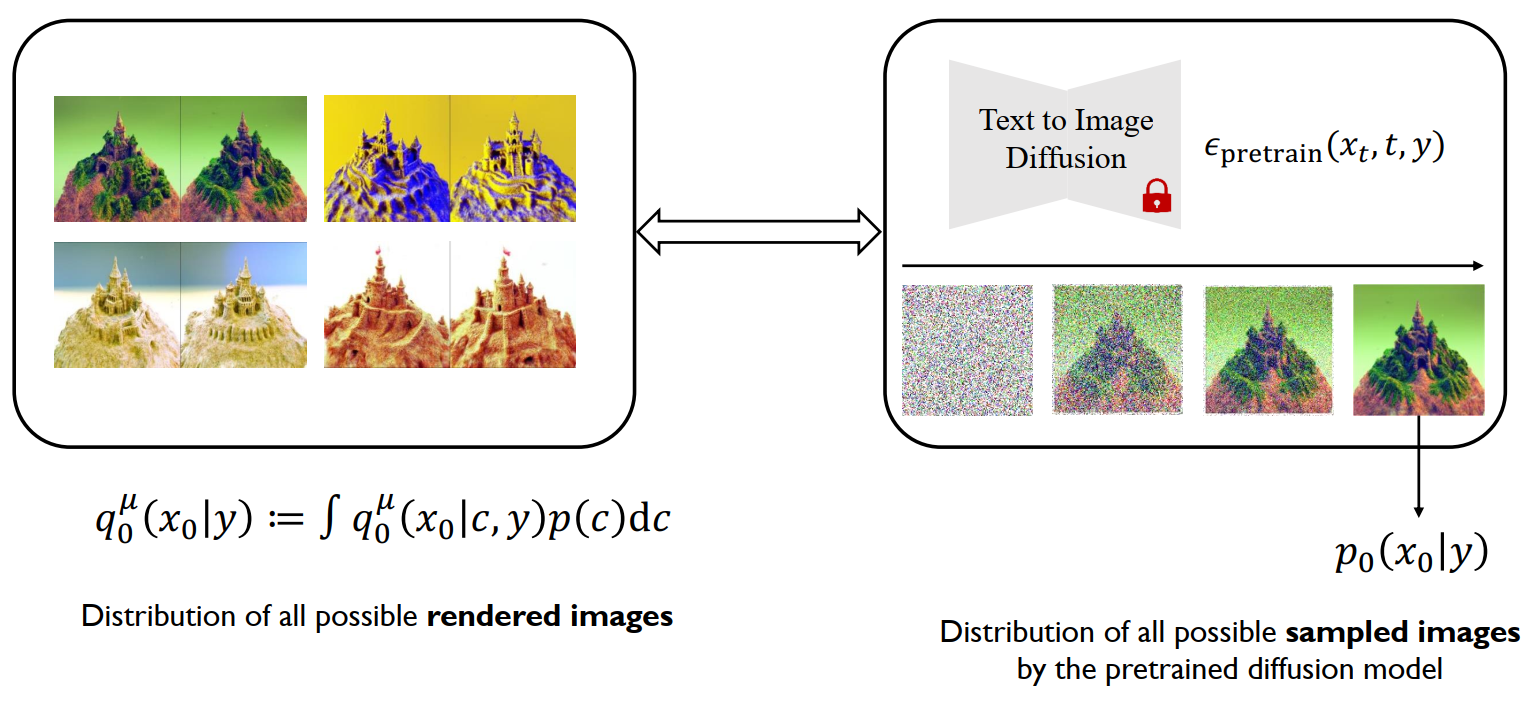
与其将整个 3D 建模当作一个点来优化，不如直接将建模看作一个分布（粒子）。优化这个 3D 分布，使其渲染出的 2D 分布与预训练模型的分布之间的 KL 散度最小。

可以从数学上看到 VSD 确实是包含了比 SDS / SJC 多的信息： \[ \text{SDS/SJC:} \quad \nabla_\theta \mathcal{L}_{\text{SDS}}(\theta) \triangleq \mathbb{E}_{t, \epsilon, c} \left[ w(t) (\boldsymbol{\epsilon}_{\text{pretrain}}(\mathbf{x}_t, t, y) - \underbrace{\boldsymbol{\epsilon}}_{\text{Gaussian noise}}) \frac{\partial \mathbf{g}(\theta, c)}{\partial \theta} \right] \]

\[ \text{VSD:} \quad \nabla_\theta \mathcal{L}_{\text{VSD}}(\theta) \triangleq \mathbb{E}_{t, \epsilon, c} \left[ w(t) (\boldsymbol{\epsilon}_{\text{pretrain}}(\mathbf{x}_t, t, y) - \underbrace{\boldsymbol{\epsilon}_\phi(\mathbf{x}_t, t, c, y)}_{\text{LoRA}}) \frac{\partial \mathbf{g}(\theta, c)}{\partial \theta} \right] \]

Lora 这个额外模型提供了比纯高斯噪音更多的信息。

并且，SDS / SJC 可以看作是 VSD 的特例：VSD 用复杂的分布，SDS / SJC 用 Dirac 分布 \(\mu(\theta|y)\approx \delta(\theta-\theta^{(1)})\)。

此外，SDS / SJC 需要过量的无分类器引导，导致结果过饱和；VSD 不需要。

最后，SDS / SJC 本质上还是通过最小化损失来找到最优模型；而 VSD 直接通过从分布采样 \(\mu^*(\theta|y)\) 进行参数优化。

ControlVideo：通过条件性控制来编辑视频

相比于图像生成，视频生成最大的问题是要保持帧与帧连贯（Temporal Consistency）。

用文字来编辑视频应该最大程度的保留原视频内容的同时与 prompt 对齐。

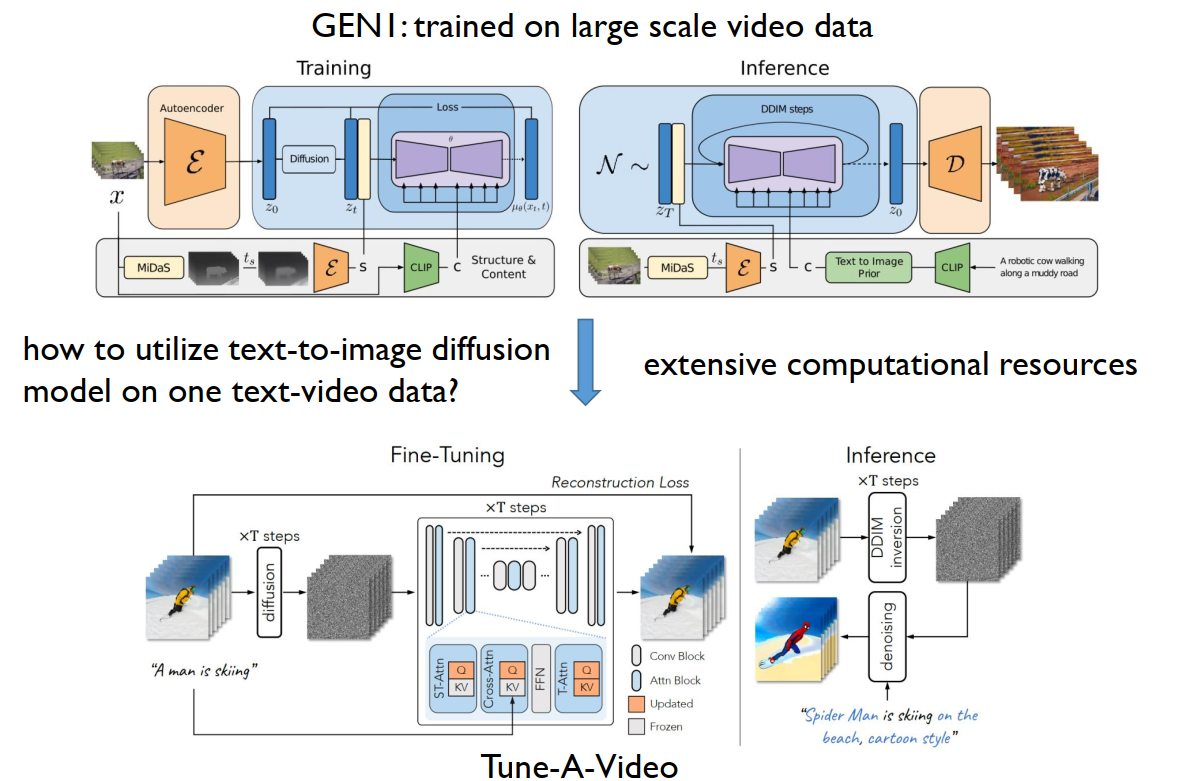
上面的 GEN I 还是无法正确的控制输出。

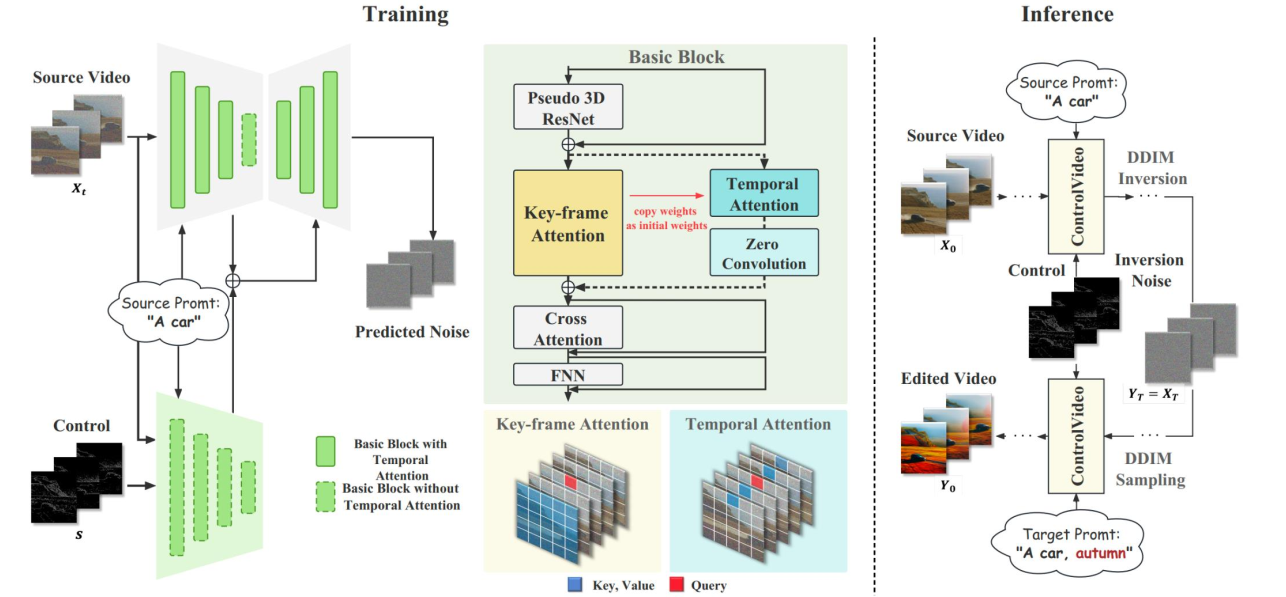
ControlVideo 引入了全注意力机制 (Full Attention)：生成第 \(i\) 帧时，Attention 会关注第一帧和前一帧，强制保持物体外观一致。

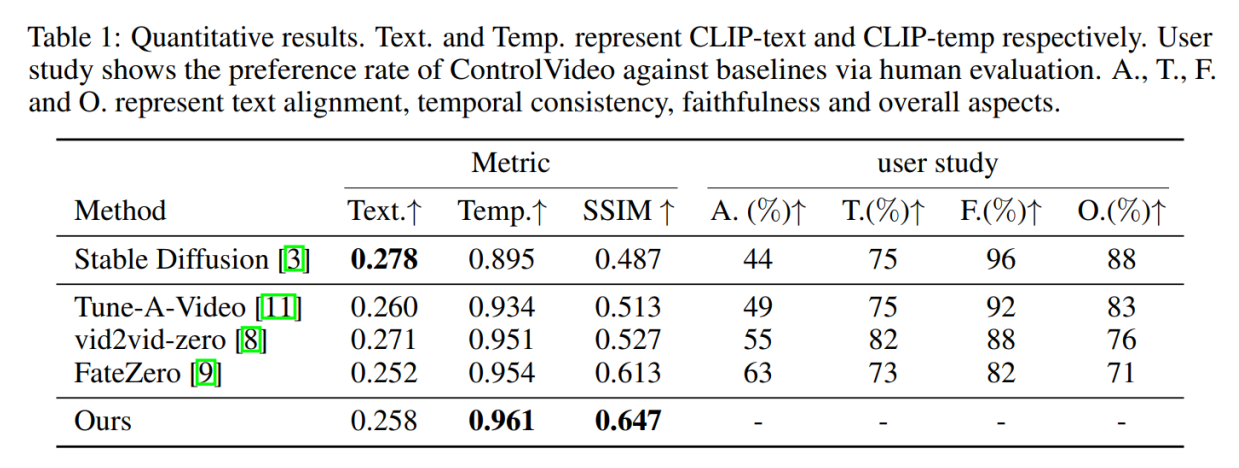
Vidu：基于 U-ViT 的 Text-2-Video 模型

基于 Vidu 生成视频的 4D 重构：

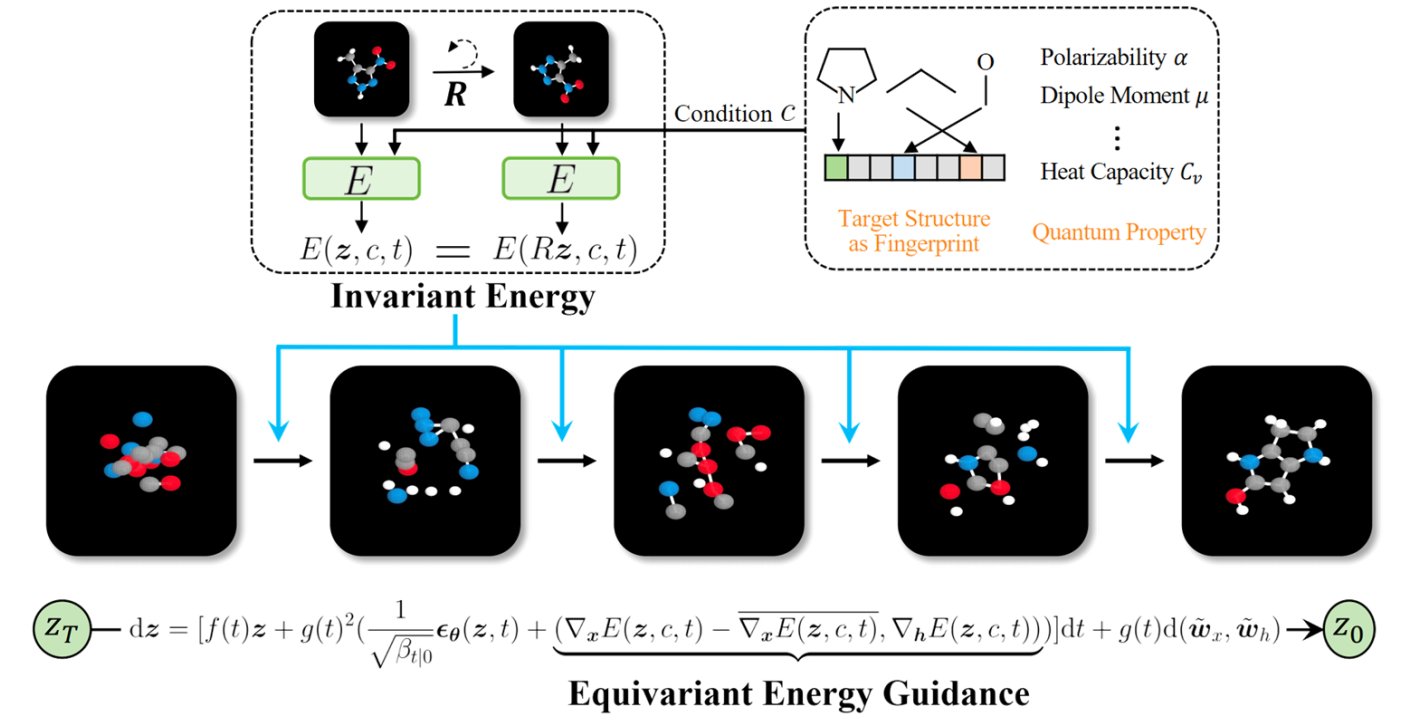
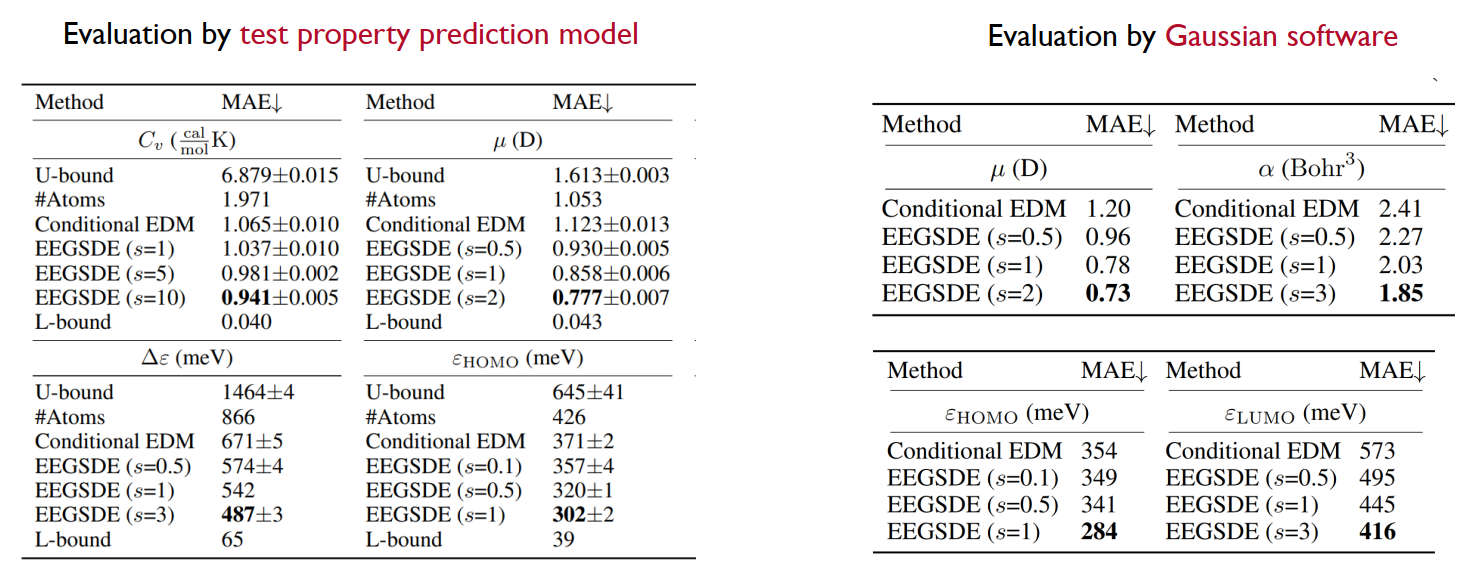
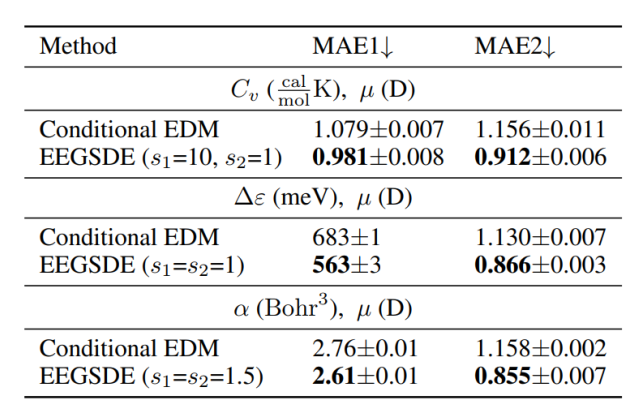
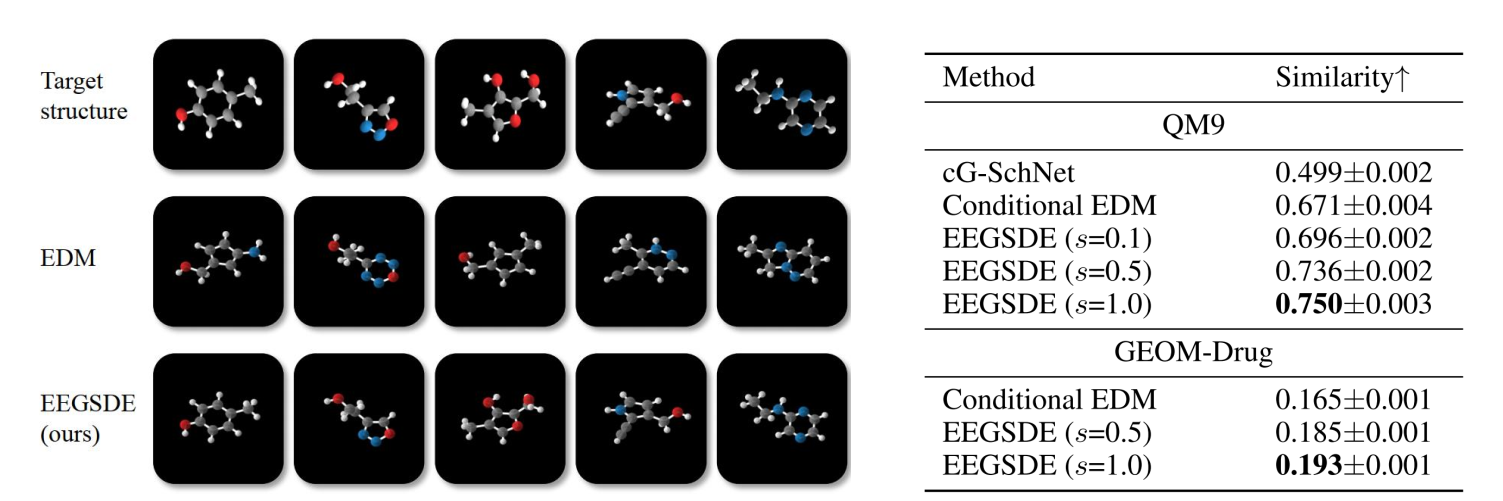
Equivariant Energy-guided SDE（EEGSDE）：分子生成

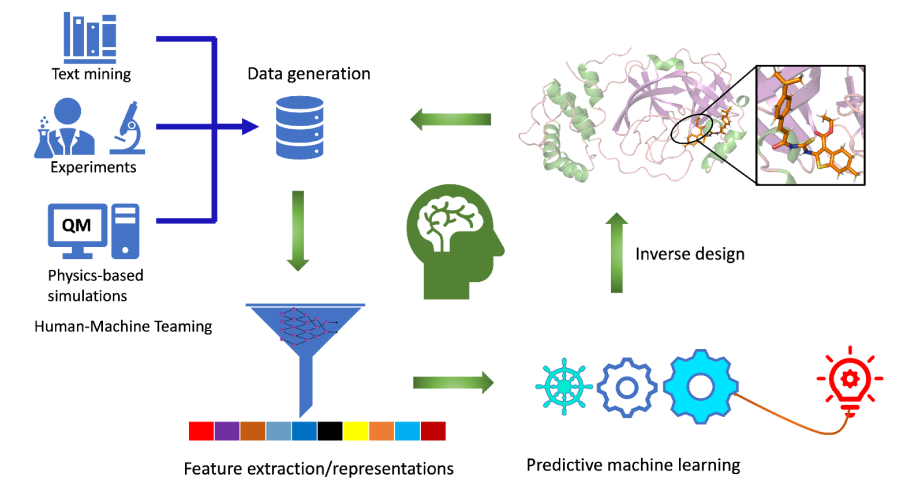
直接使用之前的模型生成的分子无法满足特定属性。

为此，可以使用一个能量函数（比如预测分子活性的分类器）来引导扩散过程，让生成的分子不仅要在化学上合理，还要具备我们要的特性。如，分子旋转后，能量应该不变。模型必须遵守这个物理对称性。

用能量函数来约束扩散模型

1. 核心要点概括

• 能量与概率的关系：在统计物理和机器学习中，概率密度 \(p(\boldsymbol{x})\) 和能量函数 \(E(\boldsymbol{x})\) 满足波尔兹曼分布关系：\(p(\boldsymbol{x}) \propto \exp(-E(\boldsymbol{x}))\)。
• 能量的物理直觉：能量越低的状态，其概率越高（越“稳定”或越符合预期）。
• 得分与能量的联系：扩散模型的核心是得分函数（Score Function） \(\nabla_{\boldsymbol{x}} \log p(\boldsymbol{x})\)，它在数学上等于能量函数梯度的负值：\(-\nabla_{\boldsymbol{x}} E(\boldsymbol{x})\)。
• 引导机制：如果你定义了一个描述物理特征（如对称性、引力、平滑度）的能量项 \(E_{\text{phys}}\)，你可以通过修改得分函数来引导生成过程趋向于低物理能量的状态。

---

2. 什么是“能量”（Energy）？

在扩散模型的背景下，“能量” \(E(\boldsymbol{x})\) 是一个标量函数，它为每一个可能的图像（或动作序列）分配一个数值：

1. 概率的负对数：简单来说，\(E(\boldsymbol{x}) = -\log p(\boldsymbol{x}) + \text{const}\)。
2. “不自然程度”的度量：如果一张图片看起来很奇怪或者不符合物理定律，它的能量就很高；如果它非常自然、符合物理逻辑，它的能量就很低。
3. 势能场：你可以把能量想象成一个起伏的地形。扩散模型的生成过程（采样）本质上就是沿着能量最陡的坡度向下滚（降能），直到落在能量最低的谷底（即高概率的数据区域）。

---

3. 如何利用能量引入物理特征？

如果你希望生成的内容符合某种物理特征（例如：物体必须受到重力落在地面上），你可以人为定义一个外部势能函数（Potential Function） \(U(\boldsymbol{x})\)：

修改得分函数（引导采样）

原本的扩散模型只根据学习到的分布移动，其方向是 \(\nabla_{\boldsymbol{x}} \log q_t(\boldsymbol{x}_t)\)。现在我们加入物理能量项的梯度：

\[\tilde{\nabla}_{\boldsymbol{x}} \log q_t(\boldsymbol{x}_t) = \underbrace{\nabla_{\boldsymbol{x}} \log q_t(\boldsymbol{x}_t)}_{\text{原来的去噪方向}} - \underbrace{\lambda \nabla_{\boldsymbol{x}} U(\boldsymbol{x})}_{\text{物理约束的引导}}\]

• \(\nabla_{\boldsymbol{x}} U(\boldsymbol{x})\)：这个项会产生一个“力”，将生成的图像推向物理能量更低（即更符合物理定律）的方向。
• 这与分类器引导（Classifier Guidance）是一致的：讲义中提到的 \(\nabla_{\boldsymbol{x}} \log p(c|\boldsymbol{x})\) 实际上就是一种特殊的“分类能量”引导。

---

4. 为什么物理特征适合用能量来表达？

• 直观建模：许多物理约束本身就是以能量形式定义的。例如：
  • 弹性约束：能量与形变成正比。
  • 流体动力学：能量与散度或涡度有关。
• 软约束（Soft Constraints）：能量法允许物理特征有一定的波动，而不是死板的硬性规定，这使得生成内容在符合物理规律的同时保持多样性。
• 即插即用：正如 DPM-Solver 是 Training-free 的一样，这种能量引导通常也不需要重新训练网络。你只需要在推理阶段，把物理能量的梯度加进采样器即可。

---

5. 总结

视角	含义	在扩散模型中的作用
概率视角	图像出现的可能性	决定模型生成的终点。
得分视角	概率增长最快的方向	指引采样器每一步怎么走。
能量视角	状态的“违和感”或物理代价	提供额外的约束力，纠正不符合物理规律的生成结果。

正如上面所看到的，扩散模型的生成过程（逆向过程）在本质上可以被理解为一种“能量最小化”的过程。

得分函数对应了能量地形的向导。扩散模型的核心任务是训练神经网络 \(\boldsymbol{\epsilon}_\theta\) 来估计得分函数 \(\nabla_{\mathbf{x}} \log q_t(\mathbf{x}_t)\)。

在物理上，如果我们定义能量 \(E(\mathbf{x}) = -\log q(\mathbf{x})\)，那么：

\[\nabla_{\mathbf{x}} \log q(\mathbf{x}) = -\nabla_{\mathbf{x}} E(\mathbf{x})\]

这里的 \(-\nabla_{\mathbf{x}} E(\mathbf{x})\) 正是能量下降最快的方向。神经网络通过预测噪声，实际上是在告诉当前的图像：“往这个方向走，能量会更低，你会看起来更像真实的图片”。

DDPM 和 DDIM 对应了两种能量场的运动方式：

• DDPM（随机）：其逆向过程对应于 Langevin Dynamics（朗之万动力学）。这就像一个球在崎岖的地形中下坡，虽然它受到指向谷底的重力（得分函数），但由于不断注入随机扰动（高斯噪声 \(d\bar{\mathbf{w}}_t\)），它不会立刻死锁在局部的坑洼里，而是能更好地探索整个能量分布。
• DDIM / DPM-Solver（直线）：通过概率流 ODE（Probability Flow ODE），图像沿着确定的能量梯度下降轨迹运动。这是一种更高效的能量最小化路径，去除了随机抖动，直奔能量最低点。

扩散模型最精妙的地方在于它不只学习一个能量场，而是分层级的建模能量。

• 噪声作为“平滑器”：在训练阶段，通过给图像加入不同程度的噪声 \(t\)，模型实际上是在学习一系列由粗到细的能量地形。
• 分步降能：在 \(t\) 较大时，能量地形是平滑的“大坑”，模型先学习确定大致的构图（全局能量最小化）；随着 \(t\) 减小，地形变得精细，模型开始修复纹理等微小细节（局部能量最小化）。

概念	扩散模型视角	能量模型视角
真实图像	高概率样本 \(x_0 \sim q_0(x_0)\)	最低能量状态 (Global Minimum)
纯噪声图像	低概率样本 \(x_T\)	最高能量状态 (High Potential)
神经网络 \(\boldsymbol{\epsilon}_\theta\)	预测加噪方向	估计能量梯度的负值
采样过程	去噪（Reverse Process）	能量最小化 (Energy Minimization)

扩散模型还能应用在强化学习

将扩散模型（DPMs）应用于强化学习（RL）是近年来机器人学和决策 AI 领域最热门的方向之一（例如 Diffusion Policy）。

扩散模型之所以在强化学习中大放异彩，主要有以下几个核心原因：

1. 核心要点概括

• 处理多峰分布（Multimodality）：传统 RL 通常假设动作服从简单的单峰高斯分布，而扩散模型可以表达复杂的、多峰的动作分布。
• 高维动作空间建模：扩散模型在处理高维数据（如像素、复杂关节轨迹）上的强大能力，使其能胜任复杂的动作规划。
• 条件引导与规划：利用引导采样（Guided Sampling）技术，可以方便地根据奖励或目标来修正生成的动作轨迹。
• 序列化决策：扩散模型可以将整个未来的动作序列看作一幅“图像”进行整体生成，从而实现长时程的规划。

---

2. 为什么 DPMs 比传统 RL 策略更好？

解决多峰行为（The Multimodal Challenge）

在很多强化学习任务中，完成同一个目标可能有多种方式（例如绕过障碍物可以从左边走，也可以从右边走）。

• 传统模型：如果使用简单的连续策略（如 SAC、PPO 中的高斯分布），模型会尝试取两种方式的平均值，导致结果指向障碍物中心，最终失败。
• 扩散模型：扩散模型通过得分函数（Score Function） \(\nabla_{\mathbf{x}} \log q_t(\mathbf{x}_t)\) 学习数据分布的坡度。它能同时保留多个高概率区域，从而生成多种可行的、互不干扰的动作方案。

利用引导采样进行规划 (Guided Sampling for Planning)

讲义中提到的分类器自由引导（Classifier-free Guidance, CFG）在 RL 中有直接的对应关系：

• 条件输入：公式中的条件 \(c\) 可以是当前的状态（State）*或者*目标（Goal）。
• 引导缩放因子 \(s\)：在 RL 中，我们可以通过增大 \(s\) 值，强制模型生成与高奖励（High Reward）目标高度一致的动作序列。
• 离线学习：在 Offline RL 中，我们可以训练模型模仿历史数据中的成功轨迹。在推理时，利用引导技术“偏向”那些高回报的轨迹。

---

3. DPMs 在 RL 中的典型应用模式

模式 A：作为动作策略（Diffusion Policy）

这是目前最直接的应用。

• 输入：当前观察到的状态 \(s\)。
• 输出：通过多步去噪生成的未来 \(K\) 步的动作序列 \(\mathbf{a}_{t:t+K}\)。
• 优势：相比于每一步只预测一个动作，这种“轨迹级生成”能保证动作在时间上的平滑性和连贯性。

模式 B：作为离线 RL 的轨迹生成器

利用扩散模型学习已知数据集的联合分布 \(q(\mathbf{x}_0, \dots, \mathbf{x}_N)\)。

• 数据增强：扩散模型可以生成与原始数据集分布一致、但从未出现过的合成轨迹，从而解决离线 RL 数据匮乏的问题。
• 得分匹配：通过最小化重权重 ELBO 目标，模型学会了向高质量轨迹（Data Manifold）靠拢的“梯度方向”。

---

4. 总结：SDE/ODE 视角的意义

正如讲义中提到的，采样过程可以看作是解一个 SDE 或 ODE：

• SDE 模式（DDPM）：在还原动作时加入随机性。在 RL 中，这相当于给智能体增加了一定的探索（Exploration）能力。
• ODE 模式（DDIM/DPM-Solver）：提供确定性的动作规划。这使得机器人能够以极快的速度（如 DPM-Solver 的 15 步采样）生成精准、可复现的工业级动作轨迹。

流模型和扩散模型本质上是同一个模型

流量匹配模型的得分蒸馏

特性	扩散模型 (Diffusion)	流量匹配 (Flow Matching)
预测目标	得分函数 \(\nabla_x \log p_t(x_t)\) 或噪声 \(\epsilon\)	速度场 \(v_t(x_t)\)
动力学方程	随机微分方程 (SDE) 或 概率流 ODE	常微分方程 (ODE)
数学联系	\(v_t(x_t)\) 可以通过 \(\epsilon\) 线性变换得到	\(v_t\) 描述了样本随时间演化的速度

1. 为什么说它们是“同一个优化目标”？

论文的核心贡献之一是提供了一个不依赖于复杂的 ODE/SDE 公式，而是基于贝叶斯规则的简单推导。

• 统一的条件期望：在生成过程中，无论是扩散模型预测噪声 \(\epsilon\) 或原始图像 \(x_0\)，还是流量匹配预测速度 \(v\)，其目标本质上都是在给定当前观测值 \(x_t\) 的情况下，估计某种形式的条件期望。

• 线性变换关系：论文指出，最优得分函数（Score function）、最优速度场（Velocity field）以及最优图像预测器（\(x_0\)-predictor）之间存在闭式的线性转换关系。这意味着：

  \[v_{opt}(x_t, t) \propto \nabla \log p_t(x_t)\]

  只要你训练好了一个流量匹配模型，你实际上也就隐式地获得了一个得分模型，反之亦然。

2. 得分蒸馏（Score Distillation）在 FM 中的应用

以往的蒸馏技术（如 LCM 的一致性蒸馏）往往需要复杂的轨迹映射。而这篇论文采用的 SiD (Score identity Distillation) 路径更为直接：

• SiD-DiT 框架：由于证明了目标的等价性，作者将 SiD 算法应用到基于 Transformer 架构（DiT）的流量匹配模型中。
• 无需微调教师模型：该方法不需要对原始的大模型（如 FLUX 或 SD3）进行昂贵的重训或参数微调，而是直接利用教师模型的预测值作为监督信号。
• 解决不稳定性：论文解决了此前将得分蒸馏应用于非扩散路径时出现的训练不稳定和噪声伪影问题，证明了得分蒸馏在流量匹配模型中同样具有稳健性。

3. 流量匹配（FM）相对于传统扩散（Diffusion）的优势

既然目标相同，为什么现在的主流模型（如 FLUX, SD3）都转向了 Flow Matching？

• 直线的采样轨迹：Flow Matching 允许定义“最优传输”（Optimal Transport）路径，使样本从噪声到图像的演变路径更接近直线。
• 更高的采样效率：相比于扩散模型弯曲的采样轨迹，直线路径意味着即使不进行复杂蒸馏，使用简单的 Euler 解算器在更少步数下也能获得较好结果，而蒸馏后则能进一步压缩至 1 步。

4. 实验涵盖的 SOTA 模型

这篇论文展示了其理论的普适性，测试对象涵盖了 2024-2025 年间最顶尖的模型：

• FLUX.1-dev (12B 参数)
• SD3.5-Medium / Large
• SANA (基于线性 Attention 的高效模型)

这些实验结果强有力地支持了“扩散与流量匹配在蒸馏加速技术上可以完全统一”的观点。

扩散是流量匹配的一个特例：

从数学框架上看，流匹配是一个更广义的框架，它涵盖了扩散模型。

• 统一目标：两者都在学习一个“向量场”。模型通过回归损失（MSE）来预测在时间 \(t\) 时的移动方向，使得初始噪声分布能够变换到数据分布。
• 数学等价性：论文证明，在高斯条件概率路径下，流匹配预测的“速度场” \(v_t(x)\) 与扩散模型预测的“得分函数” \(\nabla \log p_t(x)\)（或噪声 \(\epsilon\)）之间存在闭式的线性转换关系。
• 蒸馏的兼容性：正因为目标函数本质相同，所以针对扩散模型开发的得分蒸馏算法，只需要微调时间步的权重分配（Weighting），就能直接用于蒸馏流模型。