降维

为什么要降维

主成分分析（PCA）

自编码器（Autoencoder）

局部线性嵌入

词向量嵌入

降维问题

在处于大数据时代的今天，想直接对几千上万维度的输入进行拟合不仅是因为硬件上的困难，还是因为维度灾难（参考博客其他文章）导致的输入数据稀疏，以及噪声过大。

考虑这里：深度神经网络 - alittlebear’s blog 提到的流行假设。如果我们有办法获取这个内在维度（intrinsic dimension）的基，那么我们就可以将高维数据通过这个基来表示。下文讲到的主成分分析 PCA 本质上就就是在通过线性代数找出一组正交基的（最）近似解，当然，既然用的是线性代数，这也表示了 PCA 假设了输入空间是向量空间的，也引申出了其限制。针对此，我们在PCA后介绍几种非线性降维方法。

主成分分析（Principal Component Analysis，PCA）

如上面所说，主成分分析的概念线性代数课堂基本都会学到，具体数学推导这里就不赘述了。

但其核心思想就是通过寻找一组新的正交基（orthogonal basis）来从高维的标准欧几里得基变为这个低维基。这组正交基会最大化数据集的方差以此来进行区分（保留最多信息）。

更具体的，PCA用前 \(d\) 大的特征值来构建 \(d\) 维的正交基，从数学上可以严格证明谱（spectrum，特征值的集）对应了最大化方差的正交基。

可以看到，计算十分简单，快捷，且有效。但最大的问题还是只能解决线性数据。

自编码器（Auto-Encoder，AE）

如其名，先将 PCA 的集元素看作是潜在表示、隐表示（Latent Representation），那么 PCA 就是在学习这些潜在表示的线性组合。与其学习线性组合，不如通过神经网络的激活函数的非线性来变为学习潜在表示的非线性组合（表示和组合两者都要学习）。

基于以上思想，自编码器分为两个部分：编码器 \(\phi\) 和解码器 \(\psi\)。

• 编码器 \(\phi: \mathcal{X}\to\mathcal{F}\) 将数据映射到一个“特征码”（或者叫隐含表示、隐含变量），记为 \(h\)。
• 解码器 \(\psi: \mathcal{F}\to\mathcal{X}\) 将“特征码”隐射回原空间。

自编码器可以看作是一种特殊的神经网络，其有一层特殊的中间层，其宽度是小于输入维度（不然毫无意义）。于是，也可以通过反向传播算法 BP 来优化两个部分。

如果仅是如此可能过于简单，但是一些变种还是很有实际意义，或者可解释性还是不错的。

稀疏自编码器在自编码器的基础上进行稀疏化。

去噪自编码器通过给输入添加噪声来学习去噪的过程，这种学习方式可以有效的学习输入的特征表示而不是一些细枝末节的“细节”。现在热门的 Diffusion 模型可以看作是一连串（不同噪声等级）的去噪自编码器。

深度生成模型 这里可以看到变分自编码器 - 编码概率而不是某个具体的点，来生成新数据。

局部线性嵌入（Locally Linear Embedding，LLE）

决策树作为万能函数逼近器，本质上就是通过一个个局部线性的小线段来“锯齿状”的模拟全局函数。

类似想法也可以从数学的角度解释。在数学上流形局部同胚于一个欧几里得空间，也就是，所有局部都是可以被线性函数近似的。

词向量嵌入

自然语言的词汇量十分庞大，常用的词袋表示方法（Bag-of-Word，BoW）将第 \(i\) 维的输入作为第 \(i\) 个词出现的频率，这导致了维度十分庞大，且稀疏（大部分词都不会出现在一个输入内）。

隐含语义分析（Latent semantic analysis，LSA）

词向量嵌入假设了如果两个词出现的上下文相同，那么他们语义也相同（分布假说，distribution hypothesis）。

隐含语义分析将词-文档这个矩阵通过奇异值分解（SVD）来降维。

现在更常用的还是下一小节的基于深度神经网络的神经语言模型：

神经语言模型

从现在的眼光来看，下面两个 Word2Vec 模型作为静态嵌入（embedding）模型最大的问题就是无法区分词的多语义。如

• 我去 Bank （银行）存钱
• 我在 Bank （河岸）钓鱼

模型无法区分上述两个 Bank 不同的含义，融合在了一起。后续 ELMo 和 BERT 引用了动态上下文嵌入才解决。

连续词袋模型（Continuous bag-of-words，CBOW）

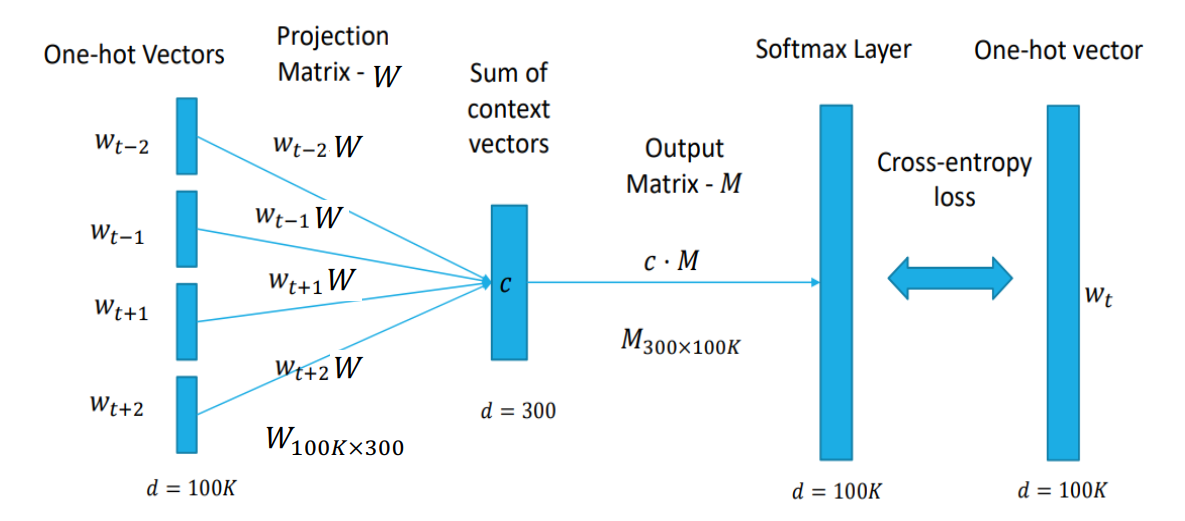
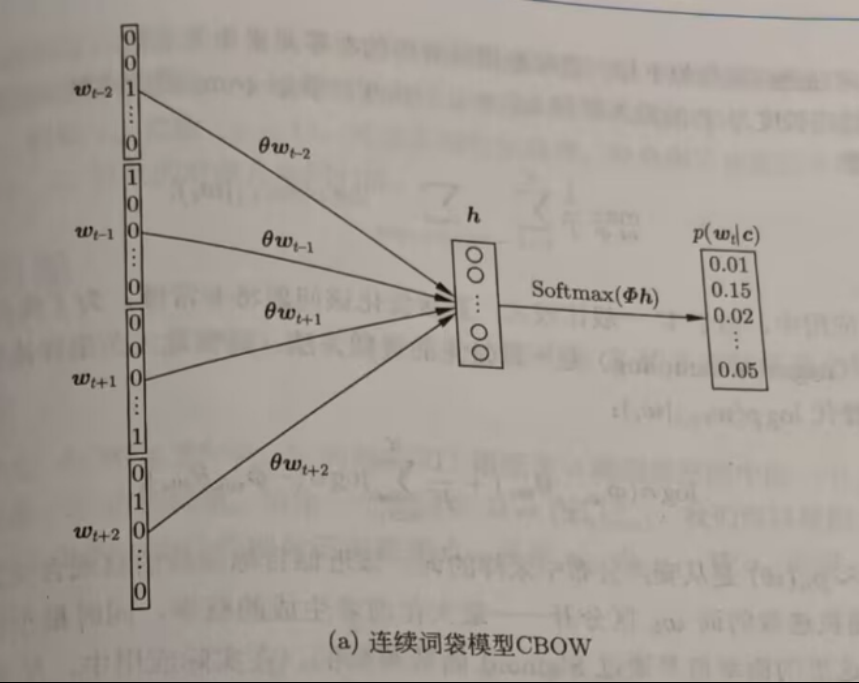
相比 BOW，CBOW 的C（连续，continuous）体现在了聚合特征向量 \(h\) 和概率输出 \(p(w_t|c)\)。

如图所示，CBOW先将 one-hot 的上下文词一起通过 \(\theta\) 映射到一个聚合特征向量 \(h\)，然后 \(h\) 通过输出投影矩阵 \(\Phi\) 映射会原空间，但不是 one-hot 而是 Softmax 的形式，最后去概率最高的作为输出。

整个过程类似于“掩码自编码器”（如 BERT，参考 深度生成模型），可以看作是一个神经网络，代表了可以通过反向传播来优化。

可以看到，上下文的几个词顺序上不重要，这导致模型失去了这方面的信息，影响输出。此外，因为平滑机制，这个模型对低频词处理不了。

Skip-gram 模型

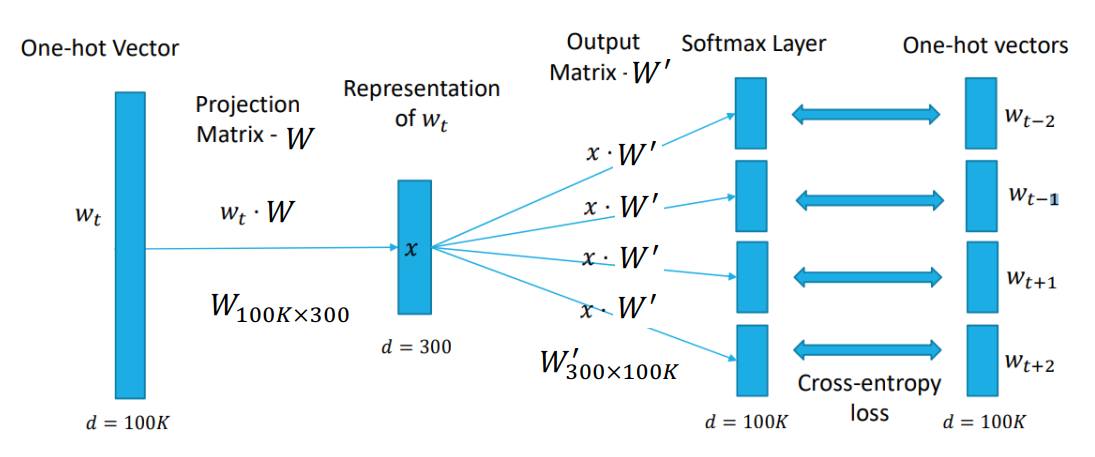
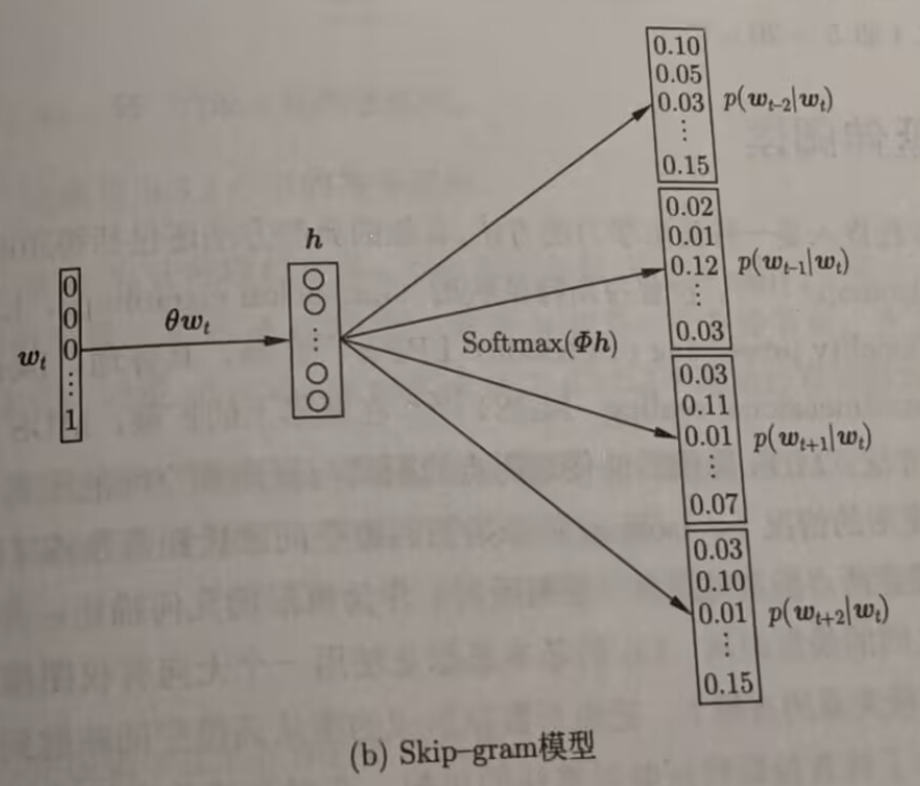
可以看到，Skip-gram 和 CBOW 较为相反。给定一个上下文中心 \(w_t\)，Skip-gram 预测上下文词。

相比之下，这个模型对低频词处理的更好，但可以看到最大的问题就是计算量太大。并且，在一个自然段中，距离远的词不一定有联系，但是这个模型假设了上下文所有词都与这个词有联系。

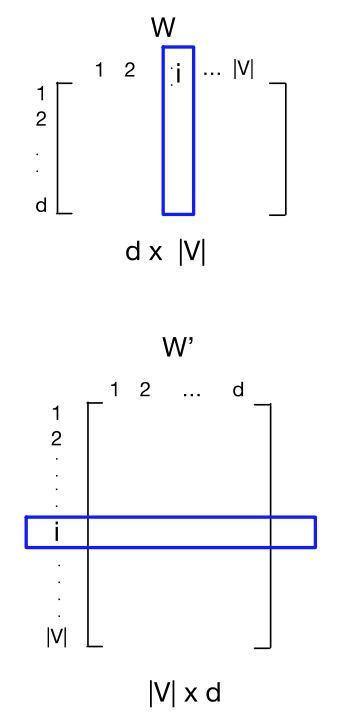
更具体的，Skip-gram 学习两个嵌入：输入的 W 和输出的 W’。

输入 \(v_i\) 的嵌入是 \(W\) 的第 \(i\) 列；词 \(i\) 的输出 \(v'\) 的嵌入是 \(W'\) 的第 \(i\) 行。

给定一个训练词序列 \(w_1,...,w_T\)，Skip-gram 的目标是最大化平均log概率： \[ \frac1T\sum_{t=1}^T\sum_{-c\le j\le c, j\ne 0}\log p(w_{t+j}|w_t) \] 其中的概率密度函数为softmax： \[ p(w_{t+j}|w_t)=\frac{\exp(v'_{w_{t+j}}v_{w_t})}{\sum_{i=1}^T\exp(v'_{w_{i}}v_{w_t})} \]

负采样（Negative Sampling）

Skip-gram 中 \(p\) 计算 Softmax 分母需要遍历词表中所有单词（如 10 万个），计算量太大。

将一个训练数据点的损失函数进行拆解，可以看到： \[ -\log p(w_{t+j}|w_t) = -\log \frac{\exp(v'_{w_{t+j}} v_{w_t})}{\sum_{i=1}^T \exp(v'_{w_i} v_{w_t})} = \underbrace{- v'_{w_{t+j}} v_{w_t}}_{\text{``positive'' pair}} + \log \sum_{i=1}^T \exp(\underbrace{v'_{w_i} v_{w_t}}_{\text{``negative'' pair}}) \] 对于 negative pair，我们没必要计算所有，可以仅选取 \(k\) 个词（5-20个） \[ \log \sigma(v'_{w_{t+j}} v_{w_t}) + \sum_{i=1}^{k} \log \sigma(-v'_{w_i} v_{w_t}) \] 可以选取距离目标单词近的词，或者对频繁出现的词进行次采样，去掉过于频繁的词（如in the）。

带有负采样的 Skip-gram（SGNS）

目标函数变为 \[ \ell = \sum_{w \in V_W} \sum_{c \in V_C} \#(w, c) \left( \log \sigma(\vec{w} \cdot \vec{c}) + k \cdot \mathbb{E}_{c_N \sim P_D} [\log \sigma(-\vec{w} \cdot \vec{c}_N)] \right) \] 其中 \(\#(w,c)\) 是上下文组合出现的次数， \(P_D\) 是观测 unigram 分布。

Word2vec 中的 SGNS（带负采样的 Skip-gram）在本质上等同于对一个特定的“词-上下文”矩阵进行矩阵分解（Matrix Factorization）。具体而言，这个矩阵的每一个元素是点间互信息（PMI）减去一个常数偏移量 \(\log k\)。

---

SGNS 的目标函数与矩阵分解视角

• 核心目标函数 (\(\ell\))：

  SGNS 的目标是最大化观测到的词对（正样本）的共现概率，同时最小化随机抽取的词对（负样本）的概率。

  • 正样本部分： \(\log \sigma(\vec{w} \cdot \vec{c})\)。通过 Sigmoid 函数 \(\sigma\) 使得词 \(\vec{w}\) 和上下文 \(\vec{c}\) 的内积尽量大。
  • 负样本部分： \(k \cdot \mathbb{E}_{c_N \sim P_D} [\log \sigma(-\vec{w} \cdot \vec{c}_N)]\)。这里 \(k\) 是负样本的数量，\(c_N\) 是从经验分布 \(P_D\) 中随机选取的噪声词。目标是让 \(\vec{w}\) 与这些噪声词的内积尽量小。

• 符号定义：

  • \(\#(w, c)\)：词 \(w\) 和上下文 \(c\) 在语料库中共同出现的次数。
  • \(P_D\)：词的经验单向分布（Unigram distribution），通常会进行 \(3/4\) 次方处理。

• 矩阵分解的视角：

  在 NLP 任务中我们通常只使用词矩阵 \(W\)（行向量），而忽略上下文矩阵 \(C\)。但从数学上看，SGNS 实际上是在尝试寻找两个低维矩阵 \(W\) 和 \(C\)，使得它们的乘积 \(W \cdot C^\top\) 逼近一个隐含的、高维的关联矩阵 \(M\)。

---

隐含矩阵 \(M\) 的真实面目

• SGNS 隐含矩阵 \(M\) = Shifted PMI：

  推导结果显示，\(M\) 矩阵中的每个元素 \(M_{ij}\) 实际上是：

  \[M_{ij} = \text{PMI}(w_i, c_j) - \log k\]

  • PMI (Pointwise Mutual Information)：点间互信息，用于衡量两个词的相关性。如果 \(w\) 和 \(c\) 经常一起出现，PMI 就很高。
  • \(\log k\) (Shift term)：这是一个偏移量，由负采样的数量 \(k\) 决定。\(k\) 越大，对关联性的“门槛”要求就越高。

• PMI 的具体计算公式：

  \[\vec{w} \cdot \vec{c} = \log \left( \frac{\#(w, c) \cdot |D|}{\#(w) \cdot \#(c)} \right) - \log k\]

  其中 \(|D|\) 是语料库的总词对数，\(\#(w)\) 和 \(\#(c)\) 分别是词和上下文的独立出现次数。

• NCE（噪声对比估算）的对比：

  与 SGNS 不同，NCE 隐式分解的是一个偏移后的对数条件概率矩阵：

  \[M_{ij}^{\text{NCE}} = \log P(w|c) - \log k\]

  这意味着 NCE 侧重于预测在给定上下文 \(c\) 时出现词 \(w\) 的概率，而 SGNS 侧重于词与上下文之间的双向相关性（联合概率）。